We included HMH Into Math Grade 7 Answer Key PDF Module 14 Understand and Apply Experimental Probability to make students experts in learning maths.
HMH Into Math Grade 7 Module 14 Answer Key Understand and Apply Experimental Probability
Probability

Game Designer
A game designer usually works as part of a team that designs and makes games. Video game designers help develop computer games for a variety of platforms, from large consoles to mobile phones. Shigeru Miyamoto, sometimes called the father of modern video games, is a Japanese game designer who has invented some of the world’s most famous and successful video games.
STEM Task:

Work with a partner to invent a simple board game for two players. Your game should use up to ten cards and/or one or two number cubes. Choose the goal of the game and decide how players move on the board. Then play the game with your partner several times. Do you think you designed a fair game? Explain why or why not.
Learning Mindset Challenge-Seeking Defines Own Challenges

A challenge is a problem that requires work and determination to solve. A challenging project may include both short- and long-term tasks. By definition, a challenge is not easy—that is why mastering a challenge is such a rewarding experience. You can feel a sense of pride because you know you accomplished something difficult. Here are some tips for tackling a challenge.
- Divide the challenge into smaller steps. Think about how each step leads to completion of the entire project or task.
- Decide how and where to find the information and knowledge you need to complete each step.
- Work with others to brainstorm, check work, share knowledge, and give and receive support.
Reflect
Question 1.
What steps did you take to complete the STEM Task?
Answer:
Question 2.
What challenges did you and your partner identify while working on the STEM Task? How did you address them?
Answer:
Go for the Gold!
In the first four levels of a video game, players roam through a castle collecting gold coins and bars. To reach Level D, a player must have a total of at least 10 more gold bars than coins. The table shows the number of coins or gold bars that Miguel collected in each of the first three levels.

Complete the table by sketching the missing gold coins and gold bars.
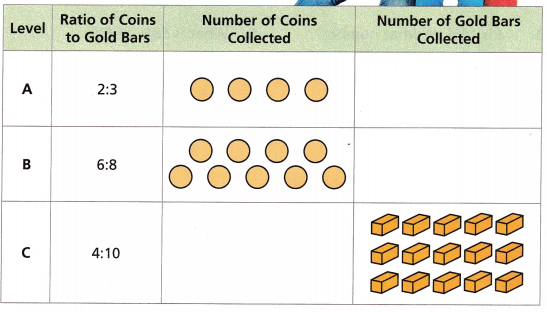
Answer:
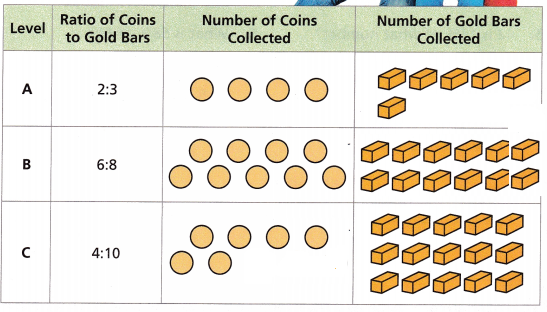
A. Ratio is 2:3 and the equivalent ratio according to the above table is 4:6
B. Ratio is 6:8 or 3:4 and the equivalent ratio according to the above table is 9:12
C. Ratio is 4:10 or 2:5 and the equivalent ratio according to the above table is 6:15
Turn and Talk Does Miguel advance to Level D? Justify your answer
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Statistical Data Collection
The dot plot shows the heights of students in one class. Use this information for Problems 1-2.
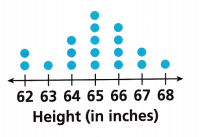
Question 1.
What unit of measure was used? How was it measured?
Answer: Mode unit of measure is used to find the average height of the students in one class.
Given data is 62, 62, 63, 64, 64, 64, 65, 65, 65, 65, 65, 66, 66, 66, 66, 67, 67, 68.
65 is repeated is 4 times.
So, the mode is 65.
Question 2.
How many students are in the class? Explain.
Answer:
By seeing the above dot plot we can say that there are 18 students in the class.
Find a Percent or a Whole
Find each value.
Question 3.
What is 45% of 200?
Answer:
45% of 200
45/100 × 200
45 × 2 = 90
Question 4.
19 is 20% of what number?
Answer:
20% = 20/100
20/100 × x = 19
20 × x = 19 × 100
2x = 190
x = 190/2
x = 95
Thus 19 is 20% of 95.
Question 5.
42 is 14% of what number?
Answer:
14% = 14/100
42 = 14/100 × x
14/100 × x = 42
14 × x = 42 × 100
14x = 4200
x = 4200/14
x = 300
Thus the unknown number is 300.
Question 6.
What is 58% of 60?
Answer:
58% of 60
58/100 × 60
5.8 × 6 = 34.8
Question 7.
What is 90% of 560?
Answer:
90% = 90/100
90/100 × 560
9 × 56 = 504
Thus 90% of 560 is 504.
Question 8.
85.5 is 45% of what number?
Answer:
If you take 45% of x is equal to 85.5 then what is the number?
In other words, we know that 45 percent of a number is 85.5
45/100 × x = 85.5
45 × x = 85.5 × 100
45x = 8550
x = 8550/45
x = 190
Thus the unknown number is 190.
Use Ratio and Rate Reasoning
Question 9.
One out of every 3 players on a soccer team is new this season. There are 15 players on the team in all. How many of the players are new?
_____________ new players
Answer:
Given,
One out of every 3 players on a soccer team is new this season. There are 15 players on the team in all.
15/3 = 5
Thus 5 players are new.
Question 10.
There are 515 students who attend Central Middle School. Three out of every 5 students live within 1 mile of the school. How many students at Central Middle School live within 1 mile of the school?
___________ students
Answer:
Given,
There are 515 students who attend Central Middle School. Three out of every 5 students live within 1 mile of the school.
We have to find how many students at Central Middle School live within 1 mile of the school.
Divide the total number of students by 3.
515/3 = 103
Thus 103 students live 1 mile away from the school.
Question 11.
How can you use proportional reasoning to write a ratio that is equivalent to another ratio?
Answer:
A ratio is the comparison of two numbers by division. Every ratio can be written as a fraction, and every fraction can be thought of as a ratio.
Example:
The ratio is 2:3 then the equivalent ratio is 4:6.