We included HMH Into Math Grade 7 Answer Key PDF Module 11 Lesson 4 Solve Multi-step Problems with Surface Area and Volume to make students experts in learning maths.
HMH Into Math Grade 7 Module 11 Lesson 4 Answer Key Solve Multi-step Problems with Surface Area and Volume
I Can solve multi-step surface area and volume problems.
Step It Out
Question 1.
A toy manufacturer makes a game that they package in a cube-shaped carton with a surface area of 54 square inches. What is the volume of the shipping carton?

A. What information is given?
(surface area / volume)
What information is needed?
(surface area / volume)
Answer:
Surface area given
Volume to be find out
B. Write the formulas for surface area and volume of a cube, where s is the length of an edge.
Surface area = 6 ![]() and Volume =
and Volume = ![]()
What do the two formulas have in common?
Answer:
s3
Explanation:
length s of the edge
Surface area = 6 s3 and Volume = s3
C. Use the given surface area to find the edge length s.

Answer:
9 in
Explanation:
Surface area = 6 x s in2
54 sq in = 6 x s in2
s = 54/6 = 9 in
D. Use the edge length to find the volume.
Volume = ![]()
Volume = ![]() =
= ![]() in3
in3
The volume is ____________ cubic inches.
Answer:
729 cubic inches.
Explanation:
Volume = s in3
Volume = 9 x 9 x 9 = 729 in3
The volume is 729 cubic inches.
Turn and Talk If the carton were a rectangular prism instead of a cube, could you find its edge lengths from its surface area? Explain.
Answer:
Yes, we find edge lengths from its surface area.
Explanation:
A cube has 6 faces which are identical squares whereas a rectangular prism has 6 faces in which all the faces are rectangles. The opposite faces in a rectangular prism are identical.
The total surface area of a cube is the area covered by all six faces of a cube.
Question 2.
Use what you know about surface area and volume to solve each problem.
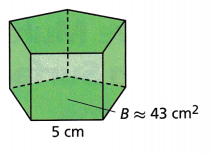
A. The regular pentagonal prism shown has a surface area of approximately 191 square centimeters. Find the approximate volume of the prism.
Use the surface area to find the approximate height.
Surface Area = 2B + Ph
![]() ≈ 2(
≈ 2(![]() ) +
) + ![]() h
h
191 ≈ ![]() + 25h
+ 25h
Subtract 86 from both sides: ![]() ≈ 25h
≈ 25h
Divide both sides by 25: ![]() ≈ h
≈ h
The approximate height h is ____________ centimeters. Use the approximate height to find the volume.
Volume = Bh ≈ ![]() ×
× ![]() =
= ![]() cm3
cm3
The volume is approximately ____________ cubic centimeters.
Answer:
180.6 cubic centimeters.
Explanation:
Surface Area = 2B + Ph
191 ≈ 2(43) + 25 h
191 ≈ 86 + 25h
Subtract 86 from both sides: 191 ≈ 25h
Divide both sides by 25: 105 ≈ h
The approximate height h is 4.2 centimeters. Use the approximate height to find the volume.
Volume = Bh ≈ 43 × 4.2 = 180.6 cm3
The volume is approximately 180.6 cubic centimeters.
B. Find the surface area of the rectangular prism with a square base.
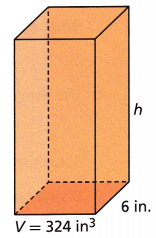
First use the volume to find the __________.
Volume = Bh
Substitute known values: ![]() = (
= (![]() )h
)h
Divide both sides by ![]() :
: ![]() = h
= h
The height is ___________ inches.
Use the height you found to determine the surface area.
Surface Area = 2B + Ph
= 2(![]() ) + (
) + (![]() ) (
) (![]() ) =
) = ![]()
The surface area is ___________ square inches.
Answer:
The surface area is 288 square inches.
Explanation:
First use the volume to find the 324 in3
Volume = Bh
Substitute known values: 324 = (36)h
Divide both sides by 36: 324 = h
The height is 9 inches.
Use the height you found to determine the surface area.
Surface Area = 2B + Ph
= 2(36) + (24) (9) = 72 + 216 = 288 in2
The surface area is 288 square inches.
Turn and Talk Make a list of strategies that help with setting up and solving word problems relating to surface area and volume. Explain each strategy.
Answer:
Surface-to-volume-ratio;
Surface area and volume with reference to the sheets;
Surface area and volume with reference to geometrical shapes.
Explanation:
As the size of an object increases, its ratio of surface area to volume decreases,
similarly as the size of an object decreases, its ratio of surface area to volume increases.
Question 3.
Reggie built the doghouse shown. He will cover the outside with weatherproof paper, then cut out the entrance. How much weatherproof paper will he need?
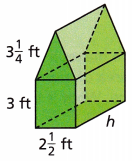
Triangle: B = 3.75 sq ft
Rectangle: B = 7.5 sq ft
Triangular prism: V = 12\(\frac{3}{16}\) cubic ft
Rectangular prism: V = 24\(\frac{3}{8}\) cubic ft
First use one of the given prism volumes to find its height. Then find the combined surface area.

A. Both prisms have the same __________, so use either volume.
Volume of rectangular prism = Bh
Substitute known values: ![]() = (
= (![]() ) h
) h
Convert the fraction to a decimal: ![]() = (
= (![]() ) h
) h
Divide both sides by ![]() :
: ![]() = h
= h
The height of both prism is ___________ inches.
Answer:
3.25 inches.
Explanation:
Volume of rectangular prism = Bh
Substitute known values: 24\(\frac{3}{8}\) = (7.5) h
Convert the fraction to a decimal: 24.375 = (7.5) h
Divide both sides by 24.375 : 7.5 = h
The height of both prism is 3.25 inches.
B. Use the height you found to determine the surface area. The triangular prism and the rectangular prism together form a
prism.
Total surface area = 2B + Ph
= 2 (![]() +
+ ![]() ) + (
) + (![]() (
(![]() ) =
) = ![]() ft2
ft2
Reggie will need __________ square feet of weatherproof paper to cover the doghouse.
Answer:
72.875 ft2
Explanation:
Total surface area = 2B + Ph
=2 (3.75 + 7.5) + (15.5) (3.25)
= 22.5 + 50.375 = 72.875 ft2
Reggie will need 72.875 square feet of weatherproof paper to cover the doghouse.
C. How much weatherproof paper will Reggie need if he does not include the floor?
Subtract the area of the floor.
Surface area = ![]() – (
– (![]() ) (
) (![]() ) =
) = ![]() ft2
ft2
Answer:
64.75 ft2
Explanation:
Surface area = 2 (3.75 + 7.5) + (13) (3.25)
= 22.5 + 42.25 = 64.75 ft2
Check Understanding
Question 1.
The surface area of a cube is 24 square inches. What is its volume?
Answer:
64 cubic inches.
Explanation:
Surface area = 6 x s in2
24 sq in = 6 x s in2
s = 24/6 = 4 in
Volume = s in3
Volume = 4 x 4 x 4 = 64 in3
The volume is 64 cubic inches.
Question 2.
A triangular prism with an equilateral triangle as its base has a volume of 64.98 cubic centimeters, a base area of 10.83 square centimeters, and a triangle edge length of 5 centimeters. What is the surface area of the prism in square centimeters?
Answer:
111.66 cm2
Explanation:
V = 64.98 cubic centimeters,
B = 10.83 square centimeters,
Volume of triangular prism = Bh
Substitute known values: 64.98 = (10.83) h
Divide both sides by 64.98 : 10.83 = h
The height of both prism is 6 cm.
S = 2B +Ph
S = 2 x 10.83 + 15 x 6
S = 21.66 + 90
S = 111.66 cm2
On Your Own
Question 3.
Use Structure Lonnie makes a regular hexagonal prism as shown with a surface area of approximately 244.8 square inches to collect his change. What is the approximate volume of change the prism will hold?

A. What is the approximate height of the prism?
Answer:
11 inches.
Explanation:
P = 6 x 3 =18 in
B = 23.4 sq in
SA = 244.8 sq in
Surface Area = 2B + Ph
244.8 ≈ 2(23.4) + 18 h
244.8 ≈ 46.8 + 18 h
Subtract 46.8 from both sides: 198 ≈ 18 h
Divide both sides by 18 : 198 ≈ h
The approximate height (h) is 11 inches.
B. What is the approximate volume of the prism?
Answer:
257.4 in3.
Explanation:
Volume = Bh ≈ 23.4 × 11 = 257.4 in3
The volume is approximately 257.4 in3.
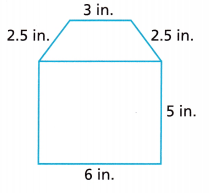
Question 4.
Use Structure A stand is being built for a sculpture at a school art show. The stand is made by placing the cube shown on top of the trapezoidal prism. The height of the prism is 3 feet. Find the volume of the composite figure.
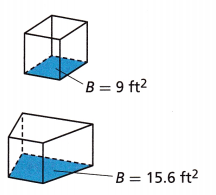
A. How high off the ground is the top of the stand?
Answer:
6 ft
Explanation:
Cube Base area B = 3 x 3 =9 sq ft
The height of the prism is 3 feet
3 + 3 = 6 ft
B. What is the volume of the composite figure?
Answer:
27 ft3
Explanation:
the volume of a prism is V = B h
V = 15.6 x 3 = 46.8 sq ft
the volume of a cube is V = a3
V = 3 x 3 x 3 = 27 ft3
the volume of the composite figure = 46.8 + 27 = 73.8 ft3
Question 5.
Social Studies The USDA estimates that 15 million households in the United States were food insecure in 2017. To help people in their community who might be food insecure, a school has a fundraiser to fill a truck with canned goods for the local food bank. If the cube-shaped boxes used to store the canned goods have a surface area of 24 square feet and the truck will hold 128 boxes, what is the maximum volume of canned goods the students can transport?
A. What is the edge length of 1 box?
Answer:
2 ft
Explanation:
Surface area of 24 square feet and the truck
A = 6a2
24 = 6 a2
Dividing by 6 on both sides
4 = a2
a = 2 ft
B. What is the volume of canned goods that the truck can carry?
Answer:
1024 ft3
Explanation:
V = a3
volume of one box
V = 2x 2 x 2 = 8 ft3
total volume for 128 box
V = 128 x 8 = 1024 ft3
Question 6.
A cube has volume 216 cubic inches. Find the surface area of the cube.
Answer:
216 sq
Explanation:
V = a3
216 = a3
a = 6 cu in
A = 6a2
A = 6 (6×6) = 216 in2
216 sq in the surface area of the cube
Question 7.
A triangular prism has a triangular base with an area of 6 square centimeters and a perimeter of 12 centimeters. The volume of the triangular prism is 18 cubic centimeters. What is the surface area of the prism?
Answer:
48 cu cm
Explanation:
B = 6 sq cm
V = Bh
h = V/B =18/6 = 3cm
P = 12 cm
V = 18 cu cm
SA = 2B + Ph
SA = 2×6 + 12 x 3
SA = 12 + 36
SA = 48 cu cm
Question 8.
An ice cube from this ice tray has a surface area of 6 square inches. What is the total volume of all the ice in the tray?

A. What is the edge length of one ice cube?
Answer:
15 cu in
Explanation:
surface area of 6 square inches
SA = 6a2
6 = 6a2
a = 1 in
V = a3
V = 1 cu in
V = 15 cu in
B. Use Structure What is the total volume of all the ice in the tray?
Answer:
15 cu in
Explanation:
V = 1 cu in
15 cubes
V = 15 cu in
Question 9.
Attend to Precision Maribelle decorates molds for making candles. The molds have the shape of open-topped regular pentagonal prisms. Each mold holds an approximate volume of 275 cubic centimeters of wax. The area of the base of a mold is approximately 27.5 square centimeters and the edge length of the base is 4 centimeters. What is the approximate surface area of a mold (not including a top)?
V = 275 cu cm
B = 27.5 sq cm
l = 4 cm
P = 4 x 5 = 20 cm
A. What is the approximate height of a mold?
Answer:
10 cm
Explanation:
V = Bh
h = V/B
h = 275/27.5
h = 10 cm
B. How should the formula for surface area be changed for this situation?
Answer:
255 cu cm
Explanation:
SA = 2B + Ph
SA = 2 x 27.5 + 20 x 10
SA = 55 + 200
SA = 255 cu cm
C. What is the approximate surface area of a mold?
Answer:
255 cu cm
Explanation:
SA = 2B + Ph
SA = 2 x 27.5 + 20 x 10
SA = 55 + 200
SA = 255 cu cm
Question 10.
STEM Noah is building a scale model of a barn for an architecture project. It is made from a trapezoidal prism on top of a rectangular prism. The volume of the barn is 390 cubic inches. The area of the base of the rectangular prism is 30 square inches, and the area of the base of the trapezoidal prism is 9 square inches. The dimensions of the front face of the barn are shown.
V = 390 cu in
The area of the base of the rectangular prism
B = 30 sq in
the area of the base of the trapezoidal prism is
B = 9 square inches
A. What is the depth of the barn model (height of the prism)?
Answer:
10 inches
Explanation:
V = Bh
390 = (30 + 9) h
h = 390/39
h = 10 in
B. What is the surface area of the model of the barn?
Answer:
318 sq in
Explanation:
SA = 2B + Ph
SA = 2 x 39 + 24 x 10
SA = 318 sq in
Question 11.
Reason A rectangular prism has a 10-inch by 2-inch base and a surface area of 424 square inches. What is the volume of a column of 8 rectangular prisms with these dimensions, stacked base-to-base?
Answer:
l = 10 in
w = 2 in
A = 20in
SA = 424 sq in
SA =
V = ?
Question 12.
Use Structure The tent shown is a triangular prism. What is the amount of space inside the tent?
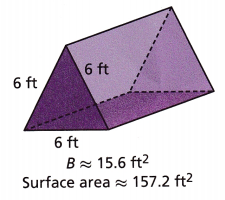
A. About how long is the tent from the front to the back?
Answer:
7.04 ft
Explanation:
SA = 2B + Ph
157.2 = 2 x 15.6 + 18 x h
157.2 – 30.4 = 18 h
126.8 = 18h
h = 7.04 ft
B. What formula will find the space inside the tent? What is the space inside the tent?
Answer:
109.89 cu ft
Explanation:
V = B h
V = 15.6 x 7.04
V = 109.89 cu ft
Question 13.
Use Structure Kristoff has a wooden cube with a volume of 1,000 cubic inches. He is going to make paper signs for each face of the cube for advertising.
A. What is the edge length of the wooden block?
Answer:
10 inches
Explanation:
V = 1000 cu in
V = a x a x a
V = 10 x 10 x 10
a = 10 in
B. What amount of paper will he need for the signs?
Answer:
600 sq in
Explanation:
SA = 6 x a x a
SA = 6 x 10 x 10
SA = 600 sq in
Question 14.
Use Structure A company stores supplies in cube-shaped boxes in a warehouse. They are stored on pallets that hold 4 boxes wide, deep, and high. The total volume of boxes is 512 cubic feet. Find the surface area of 1 box.
A. What is the volume of one cube? What is its edge length?
Answer:
Edge length 2 feet; volume is 6 cubic feet
Explanation:
V= length x width x height
512 =length x width x height = 8 x 8 x 8
4 box = 8 ft length
1 box = 2 ft length and width
surface area of 1 box is
SA = 6 x length x width
SA = 6 x 2 x 2
SA = 24 sq ft
B. What is the surface area of one box?
Answer:
24 sq ft
Explanation:
1 box = 2 ft length and width
surface area of 1 box is
SA = 6 x length x width
SA = 6 x 2 x 2
SA = 24 sq ft
Question 15.
A trapezoidal prism has a volume of 585 cubic centimeters. The area of the base is 39 square centimeters. If the base has sides measuring 4, 6.5, 6.5, and 9 centimeters, what is the surface area of the prism?
Answer:
468 sq cm
Explanation:
V = 585 cubic centimeters.
B = 39 square centimeters.
P = 4 + 6.5 + 6.5 + 9 = 26 cm
V = Bh
585 = 39 h
h = 585 / 39 = 15 cm
SA =2B + Pl
SA = 2 x 39 + 26 x 15
SA = 78 + 390 = 468 sq cm
Lesson 11.4 More Practice/Homework
Question 1.
Use Structure Holly is using wood to build the base and sides of a regular hexagonal prism-shaped herb garden with a volume of 4.3875 cubic feet. The area of the base is 5.85 square feet, and the side length of the hexagon is 1\(\frac{1}{4}\) feet long. Find the amount of wood Holly will need to complete the project.
V = 4.3875 sq ft
area of the base is 5.85 square feet
B = 5.85 square feet
length L = 1\(\frac{1}{4}\) feet = 1.25 ft
P= 6 x 1\(\frac{1}{4}\) = 6 x \(\frac{5}{4}\) = 7.5 feet
A. What is the height of the herb garden?
Answer:
0.75 ft
Explanation:
V = Bh
h = 4.3875 / 5.85
h = 0.75 ft
B. What amount of wood, in square feet, does Holly need?
Answer:
18.75 sq ft
Explanation:
SA = 2B +Ph
SA = 2 x 4.3875 + 7.5 x 1.25
SA = 8.775 + 9..375
SA = 18.75 sq ft
Question 2.
Use Structure The cargo area of the moving truck shown will be completely filled by 45 identical cube-shaped boxes. What will be the surface area of one layer of boxes on the floor of the truck bed?
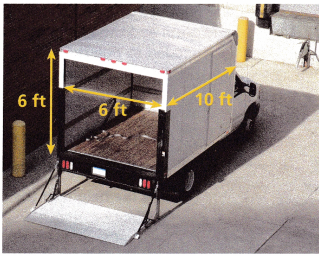
V = L x W X H
V = 6 x 6 x 10
V = 360 cu ft
A. What is the edge length of one box?
Answer:
360/45 = 8
B. What is the surface area of one layer of boxes on the floor of the truck bed?
Answer:
C. How many boxes make up this one layer?
Answer:
Question 3.
A regular hexagonal prism has a surface area of 1,714.56 square centimeters. If the area of the base is 665.28 square centimeters and the side length is 16 centimeters, what is the volume of the prism?
Answer:
Question 4.
A cube has a surface area of 96 square inches. If 16 cubes are combined to make a rectangular prism, what is the volume of the rectangular prism?
Answer:
Given,
A cube has a surface area of 96 square inches.
Surface Area = 6a²
6a² = 96
a² = 96/6
a = 4 in
Volume of a cube = a³
V = 4³
V = 64 cu. in
Volume of a prism = 64 × 16
V = 1024 cu. in
Question 5.
Math on the Spot Find the volume of milk, in cubic inches, that the carton shown can hold when it is filled up to the top of the rectangular part of the carton.
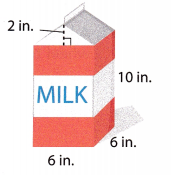
Answer:
Given,
length = 6 in
width = 6 in
height = 10 in.
V = wlh
V = 6 × 6 × 10
V = 360 cu. in
Test Prep
Question 6.
A cube has a surface area of 1,176 square inches. What is the volume of the cube?
(A) 14 in3
(B) 196 in3
(C) 1,728 in3
(D) 2,744 in3
Answer:
Option(D)
Explanation:
SA = 6 a2
1176/6 =a2
196 = a2
a = 14
V = a x a x a = 14 x 14 x 14
v = 196 x 14 = 2744 in3
Question 7.
Ina makes cakes in a pan shaped like a rectangular prism. The base of the pan is an 8-inch by 12-inch rectangle, and the volume of the pan is 288 cubic inches. Find the surface area of a cheesecake baked in this pan.
Answer:
Given,
Ina makes cakes in a pan shaped like a rectangular prism.
The base of the pan is an 8-inch by 12-inch rectangle, and
The volume of the pan is 288 cubic inches.
12 × 8 × h = 288 cu. in
96 × h = 288
h = 288/96
h = 3
Surface area = LW + LH + WH
SA = 96 × 2 + 12 × 6 + 8 × 8
SA = 192 + 72 + 64
SA = 328 sq. in
Question 8.
Suppose you are given the base area and surface area of a triangular prism and the side lengths of the triangular base. Select all the steps needed to find the volume of the prism.
(A) Find the height of the prism using the surface area formula.
(B) Find the height of the prism using the volume formula.
(C) Find the height of the triangle.
(D) Use the area of the base and the height to find the volume.
(E) Use the height of the base and the height of the prism to find the volume.
Answer:
Step 1: Find the height of the prism using the surface area formula.
(perimeter of the base × length of prism) + (2 × base area)
Step 2: Use the height and area base to find the volume
V = Area base × height
Option A and D are the correct answers.
Spiral Review
Question 9.
How many triangles can be drawn with side lengths 8 feet, 10 feet, and 21 feet?
Answer:
No, because the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
8 + 10 = 18
18 < 21
So, it is not possible to draw triangles with side lengths of 8 feet, 10 feet, and 21 feet.
Question 10.
Jared works as a landscaper. He installs a sprinkler that sprays water in a circle with an 8-foot radius. What is the approximate area covered by the sprinkler? Use 3.14 for π.
Answer:
Given,
Jared works as a landscaper.
He installs a sprinkler that sprays water in a circle with an 8-foot radius.
Area of circle = πr²
A = 3.14 × 8 × 8
A = 3.14 × 64
A = 200.96 sq. ft
Thus the area covered by the sprinkler is 200.96 ft²
Question 11.
A bike wheel has a 16-inch diameter. Approximately how far will the wheel travel in three rotations? Use 3.14 for π.
Answer:
Given,
A bike wheel has a 16-inch diameter.
3 rotations = 3 × 16 × π
3 × 16 × 3.14 = 150.72 ≈ 151 inches