Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures

We included HMH Into Math Grade 7 Answer Key PDF Module 10 Lesson 4 Areas of Composite Figures to make students experts in learning maths.

HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures

I Can break a composite figure into simple shapes and use area formulas to find its area.

Step It Out

Question 1.
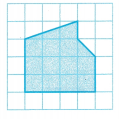
Rahim drew an outline of the front of a house on grid paper. He wants to find the area of his model.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 1$
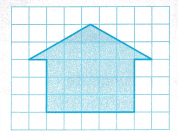
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 2$
A. Separate the composite figure into simple geometric figures. What simple geometric figures are used to form the outline?
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 3$
Answer:

Explanation:
Simple geometric figures rectangle and triangle are used to form the outline of composite figure.

B. Determine the dimensions and then find the area of each of the simple geometric figures.
Answer:
Area of rectangle = 15sq units
Area of triangle = 7 sq units

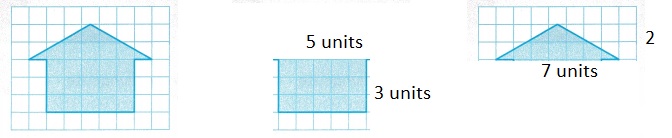
Explanation:
Area of a rectangle 5 x 3 units
A = length x width
A = 5 x 3 = 15 sq units
Area of a triangle
A = 1/2 base x height
A = 0.5 x 7 x 2
A = 7 sq units

C. Find the area of the composite figure.
Answer:
Area of composite figure = 22 sq units
Explanation:
First find the area of simple figures,
Area of a rectangle 5×3 units
A = length x width
A = 5 x 3 = 15 sq units units
Area of a triangle
A = 1/2 base x height
A = 0.5 x 7 x 2
A = 7 sq units
Area of composite figure = Rectangle are + Triangle area
Total area of the figure = 15 + 7 = 22 sq units

Turn and Talk Can you separate the composite figure into different simple geometric figures? Explain.
Answer:
Step 1: Divide the compound shape into known basic shapes.
Step 2: Find the area of each basic shape separately.
Step 3: Add all the areas of basic shapes together.
Step 4: Now, write the answer in square units of the given composite figure.

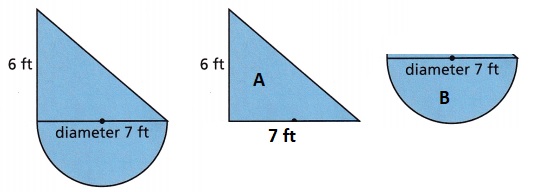
Question 2.
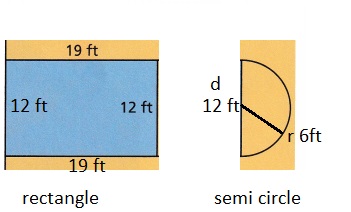
A section of a basketball court is shown.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 4$
A. Determine the simple geometric figures that are used in the composite figure.
Answer:
Rectangle and semicircle.

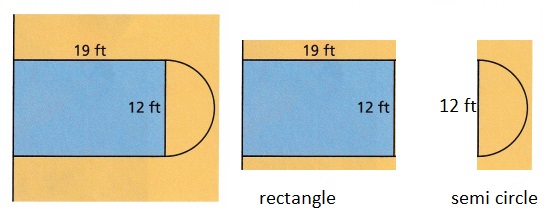
Explanation:
Rectangle has 2 sides parallel to each other.
Half of the circle is known as circle.

B. Find the dimensions of the simple geometric figures.
Answer:

Explanation:
Given length of the rectangle is 12ft, width of the rectangle is 19ft.
Diameter of circle is 12 ft, radius of circle is d/2 = 12/2 = 6ft.

C. How is the area of a semicircle related to the area of a circle with the same radius?
Answer:
Area = 36π sq ft
Explanation:
diameter = 12 ft
radius = d/2
r = 12/2
r = 6 ft
Area of a semicircle related to the area of a circle with the same radius
$A=\pi r^{2}$
A = π x 6 x 6
A = 36π sq ft

D. Find the area of the simple geometric figures to the nearest square foot. Use 3.14 for π.
Answer:
Area = 113.04 sq ft
Explanation:
$A=\pi r^{2}$
A = 3.14 x 6 x 6
A = 113.04 sq ft

E. Find the area of the composite figure.
Answer:
Area = 341.04 sq ft
Explanation:
Rectangle area A = length x width
A = 19 x 12
A = 228 sq ft
Area of the composite figure = Rectangle area + Semi circle area
A = 228 + 113.04
A = 341.04 sq ft

Turn and Talk What method do you use to determine the simple geometric figures of a composite figure?
Answer:
By splitting the simple geometric figures and then add the areas together.
Explanation:
The method to determine the simple geometric figures of a composite figure
A composite figure is made up of simple geometric shapes.
To find the area of a composite figure or other irregular-shaped figure, divide it into simple, nonoverlapping figures.
Find the area of each simpler figure, and then add the areas together to find the total area of the composite figure.

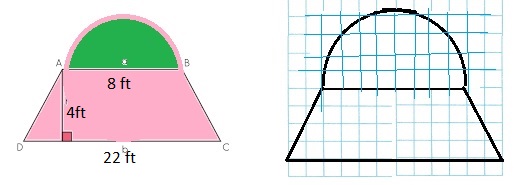
Question 3.
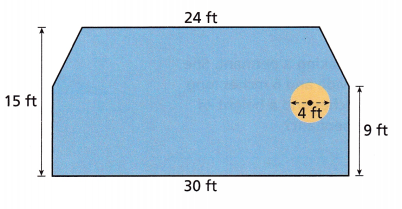
The manager of a hotel wants to put new carpet in the lobby. The dimensions of the lobby are shown. There is a statue with a circular base in the lobby that does not need to have carpet under it.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 5$
A. Determine the simple geometric figures that are in the composite figure. Find the dimensions of the simple geometric figures.
Answer:

Explanation:
Given, diameter of circle is 4ft
Dimensions of rectangular length is 9ft and width is 30ft
Dimensions of triangular length is 6ft and base is 3ft.

B. Find the areas of the simple geometric figures. Use 3.14 for π.
Answer:
Area of circle = 12.56 sq ft
Area of triangle = 9 sq ft
Area of rectangle = 30 x 9 = 270 sq ft
Explanation:
circle area $A=\pi r^{2}$
A = 3.14 x 2 x 2
Area of circle = 12.56 sq ft
Area of triangle
Area of triangle = (1/2) base x height
Area of triangle = 0.5 x 3 x 6
Area of triangle = 9 sq ft
Area of rectangle A(Rectangle) = Length x Width
A(rectangle) = 30 x 9 = 270 sq ft
C. Find the area of the lobby that needs carpet. Explain how you found the area.
Answer:
Area = 275.44 sq ft
Explanation:
The area of the lobby that needs carpet
A = A(rectangle) – A(circle) + 2 A(triangle)
A = 270 – 12.56 + 2 x 9
A = 275.44 sq ft

Check Understanding

Question 1.
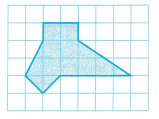
Find the area of the composite figure.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 6$
Answer:
Area = 11 sq units
Explanation:

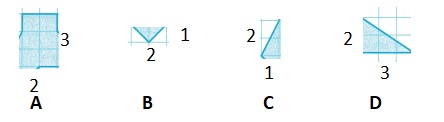
Area of composite figure
Area of fig A = length x width = 2 x 3 = 6 sq units
Area of fig B = (1/2) base x height = 0.5 x 2 x 1 = 1 sq unit
Area of fig C = (1/2) base x height = 0.5 x 2 x 1 = 1 sq unit
Area of fig D = (1/2) base x height = 0.5 x 2 x 3 = 3 sq unit
Area of composite figure = Area of (A+B+C+D+
A = 6 + 1 + 1 + 3 = 11 sq units

Question 2.
Farrah has a piece of paper that is 11 inches song and 8 inches wide. She cuts a semicircle with a radius of 4 inches out of the piece of paper. What is the area of the piece of paper she has left after the cut to the nearest hundredth? Use 314 for π.
Answer:
Area = 62.88 sq ft
Explanation:
r = 4 in
$A=\pi r^{2}$
A = 3.14 x 4 x 4
A = 50.24 sq ft
semi circle = 50.24/2 = 25.12 sq ft
Rectangle area A = length x width
A = 11 x 8
A = 88 sq ft
The area of the piece of paper she has left after the cut to the nearest hundredth
A = 88 – 25.12 sq ft
A = 62.88 sq ft

On Your Own

Question 3.
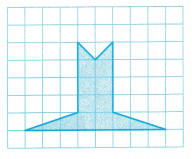
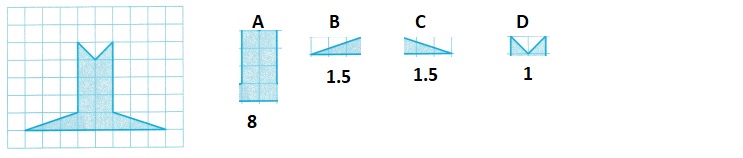
Greg designed a trophy using grid paper. What is the area of the drawing of the trophy shown?
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 7$
Answer:
Area = 12 sq units

Explanation:
Area of figure A = l x w = 2 x 4 = 8 sq units
Area of figure B =(1/2) x 1 x 3 = 1.5 sq units
Area of figure C = (1/2) x 1 x 3 = 1.5 sq units
Area of figure D = [(1/2) x 1 x 1] 2 = 1 sq units
the drawing of the trophy shown = 8 + 1.5 + 1.5 + 1 = 12 sq units

Question 4.
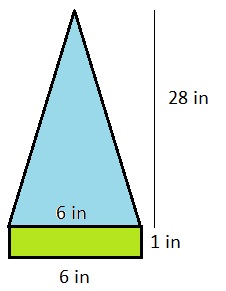
Attend to Precision Clara is making a pennant. She attaches a rectangle that is 1 inch wide and 6 inches long to a triangle that has a base of 6 inches and a height of 28 inches. What is the area of the pennant?
Answer:
Area of the pennant = 6 + 84 = 90 sq in

Explanation:
A rectangle is 1 inch wide and 6 inches long
Area = length x width
A = 6 x 1 = 6 sq in
to a triangle that has a base of 6 inches and a height of 28 inches
A =(1/2) x base x height
A = 0.5 x 6 x 28
A = 84 sq in
the area of the pennant = 6 + 84 = 90 sq in

Question 5.
Financial Literacy Mary is installing carpet in a closet for a customer. A floor plan of the closet is shown, Mary charges $5.60 per square foot of carpet, plus a $150 installation fee.
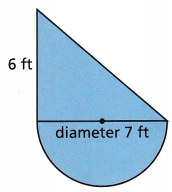
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 8$
How much should Mary charge the customer to the nearest cent? Use 3.14 for π.
Answer:
$486
Explanation:

A floor carpet area of the closet is A
A = area of figure A + area of figure B( semi $A=\pi r^{2}$ )
Area of figure A
A = (1/2) base x height
A = 0.5 x 7 x 6
A = 21 sq ft
Area of figure B
d = 7 ft
r = d/2 = 7/2 = 3.5 ft
$A=\pi r^{2}$
A = 3.14 x 3.5 x 3.5
A = 38.465 sq ft
A = area of figure A + area of figure B
A = 21 + 38.465
A = 59.465 sq ft
A = 60sq ft
Mary charges $5.60 per square foot of carpet, plus a $150 installation fee.
Total cost = 60 x 5.60 + 150
Total cost = 336 + 150 = $486

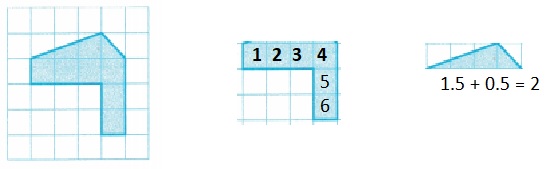
For Problems 6-9, find the area of the composite figure shown to the nearest half unit. Use 3.14 for π.

Question 6.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 9$
Answer:
13 sq units
Explanation:
Area of the composite figure is shown above
A = there are 11 complete squares = 11 sq ft

semi parts are 1.5 + 0.5 = 2sq units
Totals area of a given figure is
A = 11 + 2 = 13 sq units

Question 7.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 10$
Answer:
8 sq units
Explanation:

Area A = 6 + 2 = 8 sq units

Question 8.
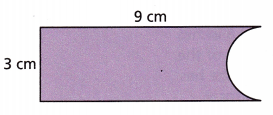
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 11$
Answer:
23.4675 sq cm
Explanation:

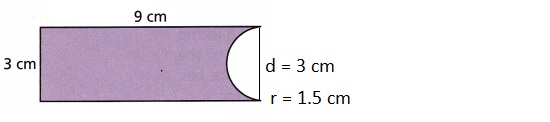
Area of a rectangle = l x w
A = 9 x 3 = 27 sq cm
$A=\pi r^{2}$
Area of a semi circle = 1/2 (3.14 x 1.5 x 1.5)
Area of semi circle = 3.5325 sq cm
Area of a given figure is = 27 – 3.5325 sq cm
A = 23.4675 sq cm

Question 9.
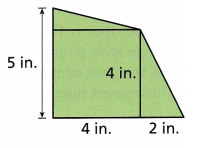
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 12$
Answer:
22 sq in
Explanation:

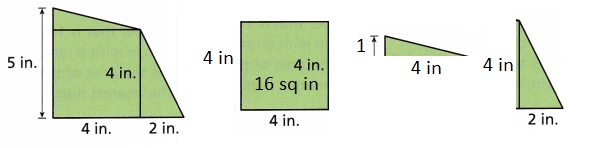
Area of square = Side x Side
A1 = 4 x 4 = 16 sq in
Area of triangle = 1/2 x base x height
A2 = 0.5 x 1 x 4 = 2 sq in
A3 = 0.5 x 2 x 4 = 4 sq in
A = A1 + A2 + A3
A = 16 + 2 + 4
A = 22 sq in
Lesson 10.4 More Practice/Homework

Question 1.
A driveway consists of two rectangles. One rectangle is 80 feet long and 15 feet wide. The other is 30 feet long and 30 feet wide. What is the area of the driveway?
Answer:
2100 sq ft
Explanation:
A rectangle is 15 ft wide and 80 inches long
Area = length x width
A1 = 80 x 15 = 1200 sq ft
A rectangle is 30 ft wide and 30 inches long
Area = length x width
A2 = 30 x 30 = 900 sq ft
the area of the driveway
A = A1 + A2
A = 1200 + 900
A = 2100 sq ft

Question 2.
Use Tools A patio is made of two sections. One is shaped like a trapezoid, and the other like a semicircle. The bases of the trapezoid are 12 feet and 8 feet. The height of the trapezoid is 4 feet. The diameter of the semicircle is the same as the trapezoid’s shorter base. Use geometry software or another tool to draw a model of the patio. Find the patio’s area. Use 3.14 for π.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 13$
Answer:
72.56 sq ft
Explanation:
The area of a trapezium can be calculated using the formula: A = ½ × (a + b) × h.

A = ½ × (a + b) × h.
A = ½ × (22 + 8) × 4.
A = 0.5 x 30 x 4
A = 60 sq ft
The area of a semicircle is half of the area of the circle. As the area of a circle is πr². So, the area of a semicircle is 1/2(πr² ), where r is the radius.
d = 8 ft
r = d/2 = 8/2 = 4 ft
A = 1/2(πr²)
A = 0.5 x 3.14 x 4 x 4
A = 12.56 sq ft
Area of patio is = area of trapezium + area of semi circle
A = 60 + 12.56
A = 72.56 sq ft

Question 3.
Open-Ended Juanita is making a ribbon as shown.
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 14$
Explain two different ways you can find the area of the ribbon. Then find the area of the ribbon.
Answer:
39 sq cm
Explanation:

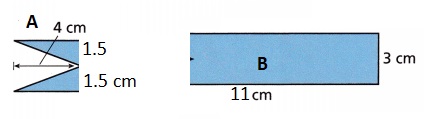
Two ways is as follows
First method:
first calculate the are of figure B
A1 = length x width
A1 = 11 x 3 = 33 sq cm
area of a triangle of figure A
A = (1/2) x base x height
A = 0.5 x 1.5 x 4 = 3 sq cm
two such triangle 3 + 3 = 6sq cm
Total are of a given ribbon is = 33 + 6 = 39 sq cm

Second way of finding the area of ribbon is

first calculate the are of figure A
A1 = length x width
A1 = 15 x 3 = 45 sq cm
area of a triangle of figure B
A = (1/2) x base x height
A = 0.5 x 3 x 4 = 6 sq cm
Total are of a given ribbon is = 45 – 6 = 39 sq cm

For Problems 4-5, find the area of the composite figure. Use 3.14 for π.

Question 4.
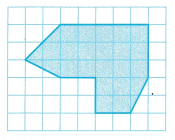
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 15$
Answer:
23 sq units
Explanation:

the area of the composite figure
20 sq units + 6×0.5 sq units
20 + 3 = 23 sq units

Question 5.
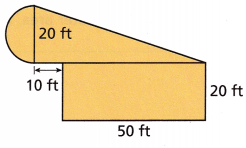
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 16$
Answer:
857 sq ft
Explanation:

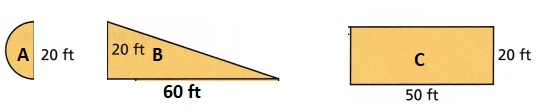
Area of figure A
d = 20 ft
r = 10 ft
$A=\pi r^{2}$
Area of a semi circle = 1/2 (3.14 x 10 x 10)
Area of semi circle = 157 sq ft
Area of figure B
A = (1/2) x base x height
A = 0.5 x 20 x 60 = 600 sq ft
Area of figure C
A3 = length x width
A3 = 50 x 20 = 100 sq ft
Total area A = A1 +A2 + A3
A = 157 + 600 + 100 = 857 sq ft

Test Prep

Question 6.
A plot of grass behind a building is shown. What is the area of the plot of grass?
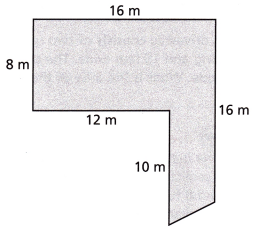
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 17$
Answer:
Area = 164 sq m
Explanation:
the area of the plot of grass is
A = A1 + A2 + A3
A1 = length x width
A1 = 8 x 16
A1 = 128 sq m
A2 = length x width
A2 = 8 x 4
A2 = 32 sq m
A3 =(1/2) base x height
A3 = 0.5 x 2 x 4
A3 = 4 sq m
the area of the plot of grass is
A = A1 + A2 + A3
A = 128 + 32 + 4 = 164 sq m

Question 7.
Eric is designing a logo for a company. The logo consists of two identical parallelograms joined at their longest sides. One of the parallelograms has a base of 2.5 centimeters and a height of 1.25 centimeters. What is the area of the logo?
Answer:
6.25 sq cm
Explanation:
parallelograms has a base of 2.5 centimeters and a height of 1.25 centimeters.
Area = base x height
Area = 2.5 x 1.25 = 3.125 sq cm
the area of the logo
3.125 sq cm + 3.125 sq cm = 6.25 sq cm
Question 8.
Find the approximate area of the composite figure. Use 3.14 for π.
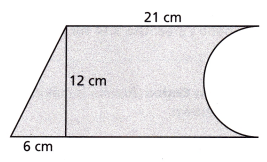
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 18$
(A) 174.96 cm²
(B) 231.48 cm²
(C) 288 cm²
(D) 344.52 cm²
Answer:
Option (B)
Explanation:
base of triangle = 6 cm
height of triangle = 12 cm
base of rectangle = 21 cm

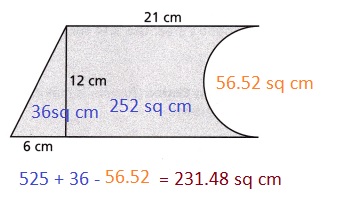
Spiral Review

Question 9.
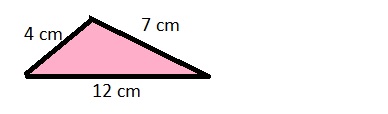
How many unique triangles can be made with sides of lengths 4 cm, 7 cm, and 12 cm: none, one, or many?
Answer:
Only one unique triangle can be made with a given lengths as shown below.
Explanation:
Triangle has 3 sides

Question 10.
A cylindrical garbage can has the dimensions shown.
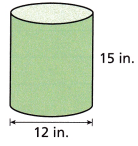
$HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures 19$
A. What is the area of a horizontal cross-section of the cylinder? Use 3.14 for π.
Answer:
Area = 113.04 sq in
Explanation:
d = 12 in
r = d/2
r = 12/2 in
r = 6 in
The area of a horizontal cross-section of the cylinder is circle
A = π. r x r
A = 3.14 x 6 x 6
A = 36 x 3.14
A = 113.04 sq in

B. What is the area of a vertical cross-section of the cylinder through the centers of the bases?
Answer:
Area = 180 sq in
Explanation:
Given, base = 12in
Length = 15 in
the area of a vertical cross-section of the cylinder is rectangle
A = length x width
A = 12 x 15
A = 180 sq in

C. Which cross-section has the greater area, and by how much?
Answer:
Area = 66.96 sq in
vertical cross section is greater then the horizontal cross section
Explanation:
A1 = 180 sq in vertical cross section
A 2= 113.04 sq in is horizontal cross section
A1 – A2 = 180 – 113.04 = 66.96 sq in

HMH Into Math Grade 7 Module 10 Lesson 4 Answer Key Areas of Composite Figures

Leave a Comment Cancel Reply