Into Math Grade 7 Module 10 Lesson 2 Answer Key Derive and Apply a Formula for the Area of a Circle

We included HMH Into Math Grade 7 Answer Key PDF Module 10 Lesson 2 Derive and Apply a Formula for the Area of a Circle to make students experts in learning maths.

HMH Into Math Grade 7 Module 10 Lesson 2 Answer Key Derive and Apply a Formula for the Area of a Circle

I Can use the area formulas for a circle to find the area of a circle if I know its radius or circumference or to find the radius or circumference if I know the area.

Spark Your Learning

A designer plans for a circular rug in a 9-foot by 9-foot square bedroom. What is the largest area of a rug that can fit in the bedroom?

Answer:
63.585 sq ft
Explanation:
Given d = 9 ft
r = d/2 = 4.5 ft
A = πr²

A = 3.14 x 4.5 x 4.5 = 63.585 sq ft

Turn and Talk How close do you think your estimate of the rug’s area was? Explain.
Answer:
63.585 sq ft or 64 sq ft
Explanation:
Given d = 9 ft
r = d/2 = 4.5 ft
A = πr²

A = 3.14 x 4.5 x 4.5 = 63.585 sq ft

Build Understanding

Question 1.
Use a parallelogram to find the area of a circle.
A. Use a compass to draw a circle on a piece of paper. Cut out the circle. Fold the circle in half three times as shown to get wedges of equal size.

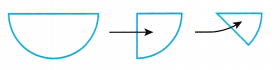
Answer:

Explanation:
Draw a circle on a piece of paper and cut out the circle.
Fold the circle in half three times as shown above to get wedges of equal size.

B. Cut the circle along the folded lines to separate the circle into eight equal wedges.
Answer:

Explanation:
By folding circle into four times, we get eight equal wedges.

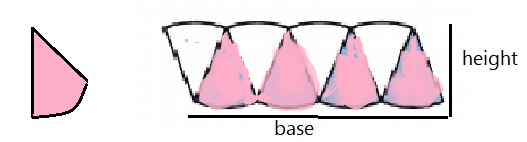
C. Arrange the wedges to form a figure resembling a parallelogram. Label the base of the parallelogram in terms of the circumference C. Label the height of the parallelogram in terms of the radius r.

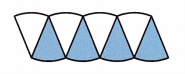
Answer:

Explanation:
When we fold the circle number of times it resemble a parallelogram,
then we observe that the base of parallelogram is the circumference and its height is the radius.

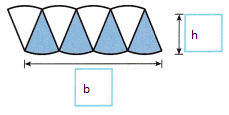
D. Use the labels on your parallelogram of wedges to substitute for b and h in the formula for area of a parallelogram.

A = b • h
A = •
Answer:
20.25 ft
Explanation:

A = b • h
A = 4.5 x 4.5
A = 20.25 ft
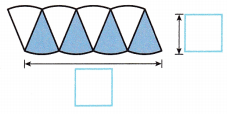
E. The formula for the circumference of a circle is C = π .
C = π A
C = π 20.25
C = 3.14 x 20.25 = 63.585 sq ft.
So half of the circumference can be written in terms of the radius as:
\(\frac{1}{2}\)C = π
Answer:
\(\frac{1}{2}\)C = π r
Explanation:
Circumference of a circle = πr²
half of the circumference = π r
F. Finally, complete the formula for the area of your parallelogram of wedges.
A = \(\frac{1}{2}\)C • r
A = • r Substitute for \(\frac{1}{2}\)C.
A = write using an exponent.
Answer:
A = πr²
Explanation:
A = \(\frac{1}{2}\)C • r
A = πr • r Substitute for \(\frac{1}{2}\)C.
A = πr² write using an exponent.

G. The parallelogram of wedges is made from a circle, so the formula for the area of a circle is:
A =
Answer:
A = πr²
Explanation:
When the parallelogram of wedges is made from a circle,
the formula for the area of a circle is:
A = base x height
A = πr x r
A = πr².

Turn and Talk How could you make your parallelogram of wedges look more like a parallelogram with straight edges?
Answer:
Make the wedges smaller, so the base looks more like a straight line than curves.
Explanation:
As we make the segments smaller and smaller,
the parallelogram becomes more of a rectangle with shorter side equal to the radius of the circle r and,
longer side πr – half of the circumference of the circle.
So, we get the formula πr2 for the area of a circle of radius r .

Step It Out

Question 2.
The formula for the area of a circle is A = πr². This formula allows you to find the area of a circle if you know the radius or diameter. How can you find the area if you know only the circumference?
A. Write the formula for circumference using r. Then solve for r.

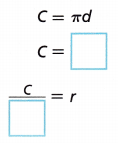
Answer:
C / 2π = r
Explanation:
C = πd
C = π2r
C / 2π = r

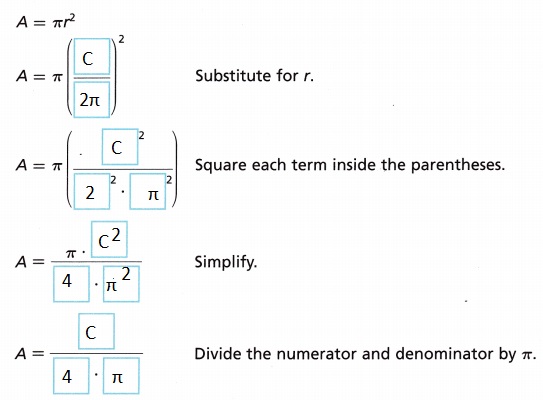
B. Substitute the expression for r into the formula for the area of a circle and simplify.

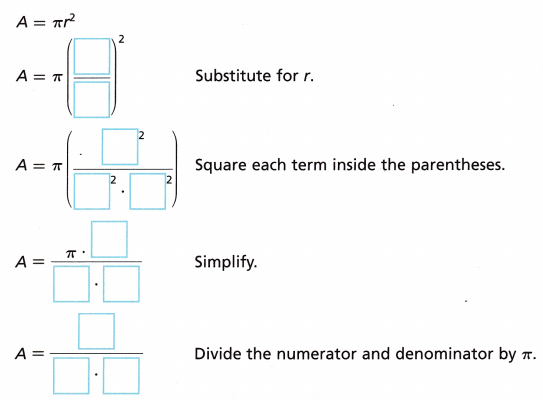
Answer:

C. Tomas visits the circular play yard for pets, as shown. Use your formula to find the area, to the nearest square meter, of this pet play yard. Use 3.14 or π.

The area is about square meters.
Answer:
336.365 sq m
Explanation:
A = C²/ 4π
A = (65 x 65)/4π
A = (65 x 65)/4 x 3.14
A = 336.365 sq m

Question 3.
Davonte wants to install a circular pool like the one shown. What is the area of the bottom of the pool to the nearest square foot? Use 3.14 for π.

A circle with a diameter of 18 feet has a radius of feet.
A = πr²
A = π()²
A ≈ • ≈ ft²
The bottom of the pool has an area of about square feet.
Answer:
254.34 square feet.
Explanation:
A circle with a diameter of 18 feet has a radius of 9 feet.
A = πr²
A = π(9)²
A ≈ 3.14 • 81 ≈ 254.34 ft²
The bottom of the pool has an area of about 254.34 square feet.

Question 4.
Louisa is making okonomiyaki, a savory type of Japanese crepe. The circumference of each crepe is about 25 centimeters. To the nearest hundredth, what is the area of each crepe? Use 3.14 for π.
Use the formula for the area of a circle in terms of the circumference.

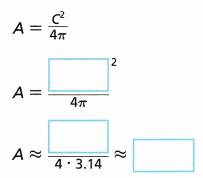
To the nearest hundredth, the area of each crepe is about square centimeters.
Answer:
The nearest hundredth, the area of each crepe is about 50 square centimeters
Explanation:

Check Understanding

Question 1.
The new circular community swimming pool has a diameter of 64 feet.
A. What is the radius of the community pool?
Answer:
32 feet
Explanation:
d= 64 feet
r = d/2
r = 64/2
r = 32 feet

B. What is the area of the surface of the pool? Use 3.14 for π.
Answer:
3215.36 sq feet
Explanation:
A = π r . r
A = 3.14 x 32 x 32
A = 3215.36 sq feet

Question 2.
To the nearest square centimeter, what is the area of a circle with a circumference of 75.36 centimeters? Use 3.14 for π.
Answer:
452.16 sq cm
Explanation:
C = circumference of 75.36 centimeters
A = C²/ 4π
A = (75.36 x 75.36)/4π
A = 5679.1296/4 x 3.14
A = 452.16 sq cm

For Problems 3-5, use the circular mirror shown.

Question 3.
To the nearest hundredth, what is the area of the mirror? Use 3.14 for π.
Answer:
Area of mirror is 176.625 sq in
Explanation:
d = 15 in
r =d/2 = 15/2 = 7.5 in
A = πr²
A = 3.14 x 7.5 x 7.5
A = 176.625 sq in

Question 4.
The mirror has a frame. The diameter of the mirror with the frame is 17 inches. To the nearest hundredth, what is the area of the mirror with the frame?
Answer:
Area of the mirror is 226.865 sq in
Explanation:
d = 17 in
r =d/2 = 17/2 = 8.5 in
A = πr²
A = 3.14 x 8.5 x 8.5
A = 226.865 sq in

Question 5.
Reason To the nearest hundredth, what is the area of the frame?
Answer:
50.25 sq in
Explanation:
Area of the frame = Area of the mirror with frame – Area of the mirror
A = 226.865 – 176.625
A = 50.24 sq in

Question 6.
A disk is shaped like a flat circular plate. Its radius is 4.25 inches. To the nearest hundredth, what is the area of the disk? Use 3.14 for π.
Answer:
Area of the desk is 56.716 sq in
Explanation:
r = 4.25 in
A =  πr²
A = 3.14 x 4.25 x 4.25
A = 56.716 sq in

Question 7.
Critique Reasoning A classmate states that if the radius of a circle is doubled, then its area is doubled. Do you agree or disagree? If you disagree, how much larger do you think the area will be?
Answer:
No, 4 times, much larger than the area.
Explanation:
r = 2r
A =  πr²
A = π(2r)²
A= 4πr²
For Problems 8-9, find the area to the nearest hundredth. Use 3.14 for π.

Question 8.

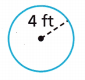
Answer:
50.24 ft²
Explanation:
r = 4 ft
A = πr²
A = π(4)²
π = 3.14
A = 3.14 x 16 = 50.24 ft²

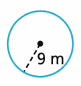
Question 9.

Answer:
254.34 ft²
Explanation:
r = 9 ft
A = πr²
A = π(9)²
π = 3.14
A = 3.14 x 81 = 254.34 ft²

For Problems 10-11, find the area. Use \(\frac{22}{7}\) for π.

Question 10.

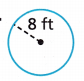
Answer:
200.96 or 201 sq ft
Explanation:
r = 8 ft
A = πr²
A = \(\frac{22}{7}\) x (8)²
A = \(\frac{22×64}{7}\) = 200.96 sq ft
A = 201 sq ft

Question 11.

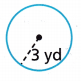
Answer:
28.28 sq ft
Explanation:
r = 3 yd
A = πr²
A = \(\frac{22}{7}\) x (3)²
A = \(\frac{22×9}{7}\) sq ft
A = 28.28 sq ft

Question 12.
Use Repeated Reasoning A lawn sprinkler waters a lawn in a circle as shown. Use \(\frac{22}{7}\) for π.

A. What is the area covered by the sprinkler?
Answer:
907.46 sq yd
Explanation:
r = 17 yd
A = πr²
A = \(\frac{22}{7}\) x (17)²
A = 907.46 sq yd
B. Suppose the water pressure is reduced so that the radius of coverage is now 11 yards. What is the area of the lawn that will now be covered?
Answer:
379.94 sq yd
Explanation:
r = 11 yd
A = πr²
A = \(\frac{22}{7}\) x (11)²
A = 379.94 sq yd

Question 13.
To the nearest hundredth, find the area of a circle with a circumference of 69.08 feet. Use 3.14 for π.
Answer:
379.94 sq ft
Explanation:
A = C² /4π
circumference of 69.08 feet, Use 3.14 for π.
A = 69.08 x 69.08 ÷ 4 x 3.14
A = 379.94 sq ft

Question 14.
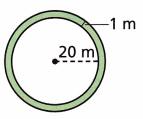
Reason A circular garden with a radius of 20 meters is surrounded by a walkway that measures 1 meter in width. Find the area of the walkway to the nearest hundredth. Use 3.14 for π.

Answer:
128.75 sq m
Explanation:
r = 20m
R = 21
A =  A2 – A1
A1 =  πr²
A1 = 3.14 x 20 x 20 = 1256 sq m
A2 = 3.14 x 21 x 21 = 1384.74 sq m
the area of the walkway
A = 128.74 sq m

Question 15.
Workers on a factory floor are painting one side of circular discs that will be placed on an assembly line. For every gallon of paint, a worker can paint an area that measures 1,256 square feet. If each disc has a radius of 2 feet, how many discs can they paint with one gallon of paint? Use 3.14 for π.
Answer:
10 discs
Explanation:
A = 1256 sq m
disc radius r = 2 ft
A = πr²
A = 3.14 x 2 x 2
A = 3.14 x 4
A = 12.56 sq ft
10 discs area = 1256 sq ft
For Problems 16-19, find the area, to the nearest hundredth, of the circle with the given circumference. Use 3.14 for π.

Question 16.
19 centimeters
Answer:
28.74 sq cm
Explanation:
C = 19 cm
A = C²/ 4π
A = (19 x 19) ÷ 4π
A = (19 x 19) ÷ 4 x 3.14
A = 28.74 sq cm

Question 17.
132 millimeters
Answer:
1,387.26 sq mm
Explanation:
C = 132 cm
A = C²/ 4π
A = (132 x 132) ÷ 4π
A = (17,424) ÷ 4 x 3.14
A = 1,387.26 sq mm

Question 18.
6.28 miles
Answer:
3.14 sq miles
Explanation:
C = 6.28 miles
A = C²/ 4π
A = (6.28 x 6.28) ÷ 4π
A = (39.4384) ÷ 4 x 3.14
A = 3.14 sq miles

Question 19.
43.96 inches
Answer:
153.86 sq in
Explanation:
C = 43.96 inches
A = C²/ 4π
A = (43.96 x 43.96) ÷ 4π
A = (1,932.4816) ÷ 4 x 3.14
A = 153.86 sq in
I’m in a Learning Mindset!

How effective were the strategies I used to find the area of a circle using the circumference of the circle?
Answer:
Easy to calculate the are of a circle, for the given r radius or C circumference value
to find the area of a circle using the circumference of the circle.

Lesson 10.2 More Practice/Homework

Question 1.
To make grape juice, water is added to a large cylindrical vat of grapes. If the diameter of the vat is 16 feet, what is the area of the base of the vat? Use 3.14 for π.

Answer:
200.96 sq ft
Explanation:
d = 16 ft
r = d/2 = 8 ft
A = πr²
A = 3.14 x 8 x 8
A = 3.14 x 64
A = 200.96 sq ft
A = 200.96 sq ft

Question 2.
Math on the Spot A group of historians is building a tepee to display at a local multicultural fair. The tepee has a height of 7 feet 4 inches at its center, and it has a circular floor of radius 14 feet. What is the area of the floor of the tepee to the nearest square foot? Use \(\frac{22}{7}\) for π.
Answer:
172 sq ft
Explanation:
The tepee h = 7.4 ft
r = 14 ft
A = πr²
A = \(\frac{22}{7}\) 7.4 x 7.4
A = 171.9464 sq ft
A = 172 sq ft

Question 3.
The face of a clock has a circumference of 14π inches. What is its area? Use 3.14 for π.
Answer:
153.61 sq in
Explanation:
A = C²/ 4π
A = 14π x 14π / 4π
A = 14 x 14 x π / 4
A = 615.44 ÷ 4
A = 153.61 sq in

Question 4.
A carpenter cuts a circle out of a piece of wood. The radius of the circle is about 23 inches. The carpenter cuts the circle into two semicircles. What is the area of one semicircle? Use 3.14 for π.
Answer:
830.53 sq in
Explanation:
A = C²/ 4π
r = 23 in
A = 3.14 x 23 x 23
A = 1661.06 sq in
Area of one semicircle = A/2
A/2  = 1661.06 ÷ 2 = 830.53 sq in

Question 5.
Use Structure Four identical circles are lined up in a row with no gaps between them such that the diameters form a segment that is 68 centimeters long. What is the combined area of all the circles to the nearest hundredth? Use 3.14 for π.
Answer:
904.46 sq cm
Explanation:

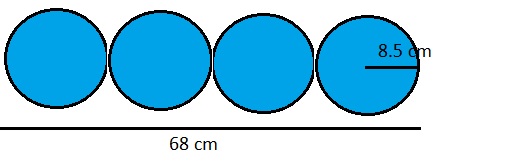
4d = 68 cm
d = 68/4
d = 17 cm
r = 8.5 cm
area of one circle
A = πr²
A = 3.14 x 8.5 x 8.5
A = 226.865 sq cm
combined area
A = 4 x 226.865
A = 904.46 sq cm

Question 6.
Ms. Flynn’s class is painting a circular canvas for the upcoming school dance. The class is estimating the area they need to paint. Its diameter is 5 feet. What is the area of the canvas to the nearest whole number? Use 3.14 for π.
Answer:
20 sq feet
Explanation:
d = 5 feet
r = 2.5 feet
the area of the canvas to the nearest whole number
A = πr²
A  = 3.14 x 2.5 x 2.5
A = 3.14 x6.25
A = 19.625 sq feet
A = 20 sq feet

For Problems 7-12, find the area of each circle described. Use 3.14 for π.

Question 7.
radius of 10 centimeters
Answer:
314 sq cm
Explanation:
r = 10 cm
A = πr²
A = 3.14 x 10 x 10 = 314 sq cm

Question 8.
diameter of 2 feet
Answer:
3.14 sq  ft
Explanation:
d = 2 ft
r = d/2 = 1 ft
A = πr²
A = 3.14 x 1 x 1
A = 3.14 sq  ft

Question 9.
circumference of 62.8 inches
Answer:
314 sq in
Explanation:
A = C²/ 4π
A = 62.8 x 62.8 ÷ 4 x 3.14
A = 3943.84 ÷12.56
A = 314 sq in

Question 10.
diameter of 8 inches
Answer:
50.24 sq in
Explanation:
d = 8 in
r = d/2 = 8/2 = 4 in
A = πr²
A = 3.14 x 4 x 4
A = 3.14 x 16
A = 50.24 sq in

Question 11.
circumference of 18.84 miles
Answer:
28.26 sq miles
Explanation:
A = C²/ 4π
A = 18.84 x 18.84 ÷ 4 x 3.14
A = 354.9456 ÷ 4 x 3.14
A = 28.26 sq miles

Question 12.
radius of 99 millimeters
Answer:
30,775.14 sq  ft
Explanation:
r= 99 mm
A = πr²
A = 3.14 x 99 x 99
A = 30,775.14 sq  ft

Test Prep

Question 13.
Larry drew a circle with a circumference of 40.82 centimeters. What is the area of the circle? Use 3.14 for π.
Answer:
Area of circle is 132.665 sq cm
Explanation:
A = C²/ 4π
A = 40.82 x 40.82 ÷ 4 x 3.14
A = 1666 ÷ 12.56
A = 132.665 sq cm

Question 14.
Safeta put a circular placemat on a table. The radius of the placemat is 7.5 inches. What is the area of the placemat? Use 3.14 for π.
Answer:
Area of placement is 176.625 sq in
Explanation:
r = 7.5 in
A = πr²
A = 3.14 x 7.5 x 7.5
A = 176.625 sq in

Question 15.
The length of the curved part of a semicircle is 25.12 inches. What is the approximate area of the semicircle? Use 3.14 for π.
(A) 25.12 in²
(B) 50.24 in²
(C) 100.48 in²
(D) 200.96 in²
Answer:
Option (D)
Explanation:
semi circle area A = πr = 25.12
r = 25.12÷3.14 = 8 in
A = πr²
A = 3.14 x 8x 8
A = 200.96 sq in

Question 16.
On a middle school basketball court, there is a large circle painted on the floor. The diameter of the circle is 12 feet. What is the area of the circle? Use 3.14 for π.
(A) 18.84 ft²
(B) 113.04 ft²
(C) 452.16 ft²
(D) 1,808.64 ft²
Answer:
Option (B)
Explanation:
diameter of circle = 12 ft
r = 122 = 6 ft
A = πr²
A = 3.14 x 6 x 6
A = 113.04 sq ft

Question 17.
Find the area of a circle with a radius of 33 millimeters. Use 3.14 for π.
Answer:
3419.46 sq mm
Explanation:
radius = 33 mm
A = πr²
A = 3.14 x 33 x 33
A = 3419.46 sq mm

Spiral Review

Question 18.
Carlos drew a figure on the smartboard and said it was a triangle with angles of 100°, 35°, and 55°. Nate said that was impossible. Who is correct? Explain.
Answer:
Nate said that was impossible, yes it is correct.
Explanation:
The principle is the sum of the internal angle of a triangle is 180°
When we add the given angles, the sum of the angles is 100°+ 35°+ 55° =190°

Question 19.
The diameter of a wheel is 3 feet. What is the circumference? Use 3.14 for π.
Answer:
9.42 sq ft
Explanation:
diameter of circle = 3 ft
r = 3÷2 = 1.5 ft
C = 2πr
C = 2 x 3.14 x 1.5
C =9.42 ft