We included HMH Into Math Grade 7 Answer Key PDF Module 10 Lesson 1 Derive and Apply Formulas for Circumference to make students experts in learning maths.
HMH Into Math Grade 7 Module 10 Lesson 1 Answer Key Derive and Apply Formulas for Circumference
I Can use the circumference formulas C = πd and C = 2πr to solve for C, r, or d when the value of the other variable is given.
Spark Your Learning
A woodworker has twelve spokes. To make the wheel’s rim, there are two pieces of wood that can be curved using steam. They are 6 feet and 8 feet long.

The measure along the spokes from the center to the inside of the rim is shown. Is the 6-foot piece of wood long enough to curve around for the wheel’s rim? Is the 8-foot piece of wood long enough? Use measuring tools, large paper, and string to help solve.
Answer:
8-foot piece of wood long is enough, as it require only 6.285 ft
Explanation:
r = 1 ft
Circumference of the wheel
circumference formulas C = πd and C = 2πr
C = 2 x 22/7 x 1
C = 44 / 7
C = 6.2857 ft
8-foot piece of wood long enough
Turn and Talk Did this experiment give you an idea of how much longer a string that makes up the rim of a wheel must be than one of the spokes? Explain.
Answer:
5.2857 ft much longer a string that makes up the rim of a wheel must be than one of the spokes
Explanation:
r = 1 ft
Circumference of the wheel
circumference formulas C = πd and C = 2πr
C = 2 x 22/7 x 1
C = 44 / 7
C = 6.2857 ft
as r = 1 ft
6.285 – 1 = 5.2857 ft
5.2857 ft much longer a string that makes up the rim of a wheel must be than one of the spokes
Build Understanding
Question 1.
Find circular objects or objects that have a circular face. For each object, follow the steps to complete the table.
Connect to Vocabulary
The circumference of a circle is like the perimeter of a rectangle; it is the distance around the figure.
A. List the name of the object in the table.
Answer:
small bowl
B. Measure and record the circumference of the circular face.
Answer:
C = 16 in
C. Measure and record the diameter of the circular face.
Answer:
d = 5 in
D. Calculate the ratio of the circumference to the diameter. Write the ratio as a decimal in the table.

Answer:
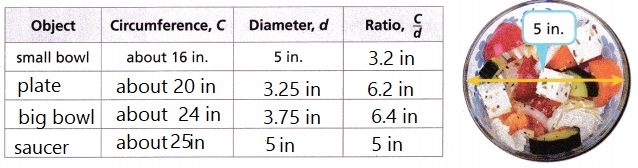
Explanation:
Circumference of the given object
circumference formulas C = πd and C = 2πr
Turn and Talk Describe what you notice about the ratio \(\frac{C}{d}\) in your table. Does the relationship between the circumference and diameter of a circle appear to be proportional? Explain.
Answer:
Yes, the relationship between the circumference and diameter of a circle appear to be proportional.
Explanation:
\(\frac{C}{d}\)
Circumference C = 2πr
C = π d
π = \(\frac{C}{d}\) = 3.14
Question 2.
Pi, represented by the symbol π, is the ratio of a circle’s circumference to its diameter. You can use this relationship to find a formula for circumference.
Connect to Vocabulary
The ratio of circumference to diameter, \(\frac{C}{d}\), is the same for all circles and is called π or pi The value of π can be approximated by 3.14 or by \(\frac{22}{7}\).
A. Write an equation for π using C for circumference and d for diameter.
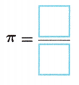
Answer:
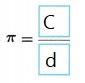
Explanation:
circumference formulas C = πd
π = \(\frac{C}{d}\)
B. How can you rewrite the equation as a formula for circumference C?
C = ![]() •
• ![]()
Answer:
C = π • d
Explanation:
Formula for circumference:
C = π • d
C. How are diameter and radius related?
The diameter is equal to ____________ times the radius.
Answer:
2r
Explanation:
The diameter is equal to two times the radius
d = 2r
D. Rewrite your equation for C in terms of the radius r.
C = ![]() • 2
• 2 ![]()
Answer:
C = π • 2 r
Explanation:
C = π • 2 r
C is the circumference and r is the radius
C = 2πr
Step It Out
Question 3.
Juanita wants to put a circular fence around the edge of the circular garden shown. How much fencing will she need to the nearest foot? Use 3.14 for π.

C = πd
C ≈ 3.14 • ![]()
C ≈ ![]()
Juanita will need about ___________ feet of fencing.
Answer:
44 feet of fencing.
Explanation:
C = πd
C ≈ 3.14 • 14
C ≈ 43.96
C ≈ 44 feet
Juanita will need about 44 feet of fencing.
Question 4.
The circumference of a men’s adult basketball hoop is about 56.52 inches. The diameter of a basketball is about 9.55 inches. Show that the ball can fit through the hoop. Use 3.14 for π.
Find the diameter of the hoop using C = πd.
C = πd
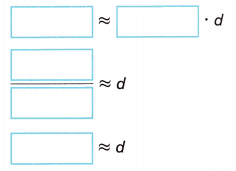
The diameter of the hoop is about inches, which (is /is not) greater than the diameter of the basketball.
Answer:
Hoop is greater than the diameter of the basketball.
Explanation:

Check Understanding
Question 1.
At a park, the jogging trail is a circle with a radius of 200 meters. How far is it around the trail? Use 3.14 for π. Show your work.
Answer:
Trail is around 1,256 m
Explanation:
r = 200 m
3.14 = π.
C = 2.π.r
C = 2 x 3.14 x 200
C = 1,256 m
Question 2.
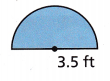
A contractor is installing a semicircular window with a radius of 3.5 feet. Find the distance around the window. Use \(\frac{22}{7}\) for π. Explain your answer.
Answer:
Distance around window is 22 ft
Explanation:
r = 3.5 ft
semicircular window
d = 2 x r
d = 2 x 3.5 = 7 ft
C = \(\frac{22}{7}\) x 7
C = 22 ft
On Your Own
Question 3.
Toni rides the Ferris wheel shown for 15 revolutions.

A. How far does Toni travel in one revolution? Use \(\frac{22}{7}\) for π.
Answer:
352 ft
Explanation:
Toni travel in one revolution = C = 2πr
C = 2 \(\frac{22}{7}\) 56
C = 2 x 22 x 8
C = 44 x 8
C = 352 ft
B. How far does Toni travel for the entire ride?
Answer:
5,280 ft
Explanation:
Toni travel in one revolution = C = 2πr
C = 2 \(\frac{22}{7}\) 56
C = 352 ft
Toni rides the Ferris wheel shown for 15 revolutions.
352 x 15 = 5,280 ft
Question 4.
Reason Paul is making a ball-toss game for his club booth at the fair. He wants to make the circumference of the holes at least 3 inches greater but not more than 4 inches greater than the circumference of the ball. One person suggests that Paul can make the diameter of the hole 1 inch greater than that of the ball. Another suggests the diameter should be 2 inches greater. Which suggestion should Paul choose? Explain.
Answer:
Yes, the diameter of the 1 inch hole is greater than that of the ball.
Explanation:
circumference of the holes at least 3 inches greater but not more than 4 inches greater than the circumference,
of the ball ,then the diameter of the hole 1 inch greater than that of the ball is correct
Explanation:
C = 2πr
d = 2r
if the diameter of the hole 1 inch greater than that of the ball.
C = π(d + 1)
C = πd + π
C + 3.14 = πd
the diameter of the hole 2 inch greater than that of the ball.
C = π(d + 2)
C = πd + 2π
C + 6.28 = πd
Question 5.
Health and Fitness Juan runs a total of 11,775 feet around a circular track, burning 12 calories each lap. The track’s diameter is 150 feet. How many calories does Juan burn? Round your answer to the nearest whole number. Use 3.14 for π.
Answer:
300 calories
Explanation:
d = 150 ft
C = 2πr
C = 3.14 x 150 = 471
11775 / 471 = 25 laps
burning 12 calories each lap.
total calories does Juan burn
= 25 x 12 = 300 calories
For Problems 6-7, find the circumference. Round your answer to the nearest hundredth. Use 3.14 for π.
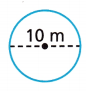
Question 6.
Answer:
31.4 m
Explanation:
C = 2πr
d = 2r
r = d/2
r = 10/2 = 5 m
C = 2πr
C = 2 x 3.14 x 5 = 31.4 m
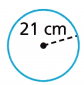
Question 7.
Answer:
131.88 cm
Explanation:
r = 21 cm
C = 2πr
C = 2 x 3.14 x 21 = 131.88 cm
I’m in a Learning Mindset!
Did my strategy for deriving and applying circumferences work? How did I adjust my strategy when I got stuck?
Answer:
yes, deriving and applying circumferences works.
When struck once again go through the problem.
Lesson 10.1 More Practice/Homework
Question 1.
Math on the Spot A counter recorded 254 revolutions of the bicycle wheel shown. How far did the bicycle travel? Use \(\frac{22}{7}\) for π.

A. How far does the wheel roll for one tire revolution?
Answer:
3.928 ft
Explanation:
Use \(\frac{22}{7}\) for π.
d = \(\frac{5}{4}\) = 1.25 ft
r = \(\frac{d}{2}\) = \(\frac{1.25}{2}\) = 0.625
C = 2πr
C = 2 x \(\frac{22}{7}\) x 0.625 = 3.928 ft
B. What is the total distance recorded?
Answer:
997.712ft
Explanation:
A counter recorded 254 revolutions of the bicycle wheel shown.
total distance recorded = 254 x 3.928 = 997.712ft
Question 2.
Use Structure Hans opens a circular window that is 3.5 feet across at its widest point. What is the circumference of the window to the nearest whole number? Use 3.14 for π.
Answer:
22 ft
Explanation:
a circular window that is 3.5 feet across at its widest point
d = 3.5 ft
C = 2πr
C = 2 x 3.14 x 3.5 = 21.98 ft or 22 ft
Question 3.
Use Structure Ting is making a circular garden with a radius of 6 feet. How far across is the garden at its widest point? What is the length of edging material to the nearest hundredth needed to enclose the garden? Use 3.14 for π.
Answer:
37.68 ft
Explanation:
r = 6 ft
C = 2πr
C = 2 x 3.14 x 6 = 37.68 ft
For Problems 4-9, find the circumference. Round your answer to the nearest hundredth. Use 3.14 for π.
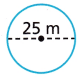
Question 4.
Answer:
78.5 m
Explanation:
d = 2r = 25
r = 25/2 m
r = 12.5
C = 2πr
C = 2 x 3.14 x 12.5 = 78.5 m
Question 5.

Answer:
28.26 cm
Explanation:
r = 4.5 cm
C = 2πr
C = 2 x 3.14 x 4.5 = 28.26 cm
Question 6.

Answer:
175.84 in
Explanation:
r = 28 in
C = 2πr
C = 2 x 3.14 x 28 = 175.84 in
Question 7.
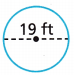
Answer:
59.66 ft
Explanation:
d = 2r = 19
r = 19/2 m
r = 9.5
C = 2πr
C = 2 x 3.14 x 9.5 = 59.66 ft
Question 8.
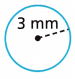
Answer:
18.84 mm
Explanation:
r = 28 in
C = 2πr
C = 2 x 3.14 x 3 = 18.84 mm
Question 9.

Answer:
219.8 in
Explanation:
r = 35 in
C = 2πr
C = 2 x 3.14 x 35 = 219.8 in
Test Prep
Question 10.
What is the circumference of the circle to the nearest hundredth? Use 3.14 for π.
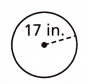
(A) 26.69 in.
(B) 53.38 in.
(C) 106.76 in.
(D) 907.46 in.
Answer:
Option(C)
Explanation:
r = 17 in
C = 2πr
C = 2 x 3.14 x 17 = 106.76 in
Question 11.
Randy is designing a circular garden that is 18 feet in diameter. He is buying plastic edging that costs $1.50 per foot. He can only buy edging in whole-foot amounts. How much does it cost Randy to buy edging for his garden? Use 3.14 for π.
Answer:
$ 84.78
Explanation:
d = 18 ft
C = 2πr
C = 2 x 3.14 x 9 = 56.52 ft
He is buying plastic edging that costs $1.50 per foot.
He can only buy edging in whole-foot amounts.
= 56.52 x 1.50 = $ 84.78
For Problems 12 and 13, find the circumference of each circle to the nearest hundredth. Use 3.14 for π.
Question 12.
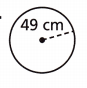
Answer:
307.72 cm
Explanation:
r = 28 in
C = 2πr
C = 2 x 3.14 x 49 = 307.72 cm
Question 13.
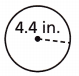
Answer:
27.632 in
Explanation:
r = 4.4 in
C = 2πr
C = 2 x 3.14 x 4.4 = 27.632 in
Spiral Review
Question 14.
Nada is making square coasters with sides of 3 inches. On each coaster is a circular design. What is the radius of the largest circle that fits on one of the coasters?
Answer:
1.5 inches
Explanation :
On squares of 3 inch side we can draw a circle of 3 inch diameter
the diameter of largest circle is 3 inch
so the radius will be diameter ÷ 2
radius of the largest circle which can be drawn on the square coasters is 3 ÷ 2 = 1.5 inch
Question 15.
In the circle in the diagram, \(\overline{A C}\) is the diameter and \(\overline{B D}\) is the radius that splits the upper semicircle in half. What is the measure of ∠ABD?
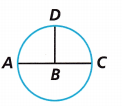
Answer:
The measure of ∠ABD = 90 degrees
Explanation:
Total angle in a circle is 360 degrees
If semi circle or AC is 180 degrees,
then ABD is a part of 1/4 of a circle as shown below
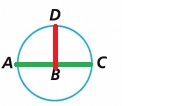
So, The measure of ∠ABD = 90 degrees