We included HMH Into Math Grade 7 Answer Key PDF Module 1 Review to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Review Answer Key
Vocabulary
constant of proportionality
proportional relationship
ratio
scale
scale drawing
unit rate
Choose the correct term from the Vocabulary box.
Question 1.
the quantity k in a relationship described by an equation of the form y = kx
Answer: Constant of proportionality the quantity k in a relationship described by an equation of the form y = kx.
Question 2.
a rate in which the second quantity is one unit
________________
Answer: Unit rate is a rate in which the second quantity is one unit.
Question 3.
a relationship between two quantities in which the rate of change or the ratio of one quantity to the other is constant
________________
Answer: A relationship between two quantities in which the rate of change or the ratio of one quantity to the other is constant is called a proportional relationship.
Concepts and Skills
Question 4.
Which ratio is equivalent to the scale 3 in.: 1 ft?
![]()
Answer:
1/4 ÷ 2/3 = 3/8
2 ÷ 2/3 = 2 × 3/2 = 3/1 = 3:1
Option B is the correct answer.
Question 5.
Use Tools A news radio program has 3 commercial breaks per half-hour of programming. What is the unit rate of commercials to hours of programming? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
Given,
A news radio program has 3 commercial breaks per half-hour of programming.
3 breaks = 1/2 hours
For 1 hour
1 = 3 × 2 = 6 breaks
1 hour = 6 breaks
Now for the Unit rate of a break to an hour is
6 breaks = 1 hour
1 break = 1/6 hours
Thus the answer is 1/6 hours
Question 6.
A recipe calls for 2 cups of sugar for \(\frac{1}{4}\) cup of butter. What is the unit rate for sugar to butter? __________
Answer:
A recipe calls for 2 cups of sugar for \(\frac{1}{4}\) cup of butter.
\(\frac{1}{4}\) = 0.25
0.25/2 = 0.125
Unit rate of sugar to butter is 1 to 0.125
Divide both sides by 0.25
0.25/0.25 = 1
2/0.25 = 6
Unit rate of butter to sugar is to
Question 7.
Jana and Jenn are training to run a race. Jana runs 3 miles in \(\frac{1}{3}\) hour. Jenn runs 5 miles in \(\frac{3}{4}\) hour. Who runs faster, and what is the unit rate of her speed in minutes per mile? ________________
Answer:
Given,
Jana and Jenn are training to run a race.
Jana runs 3 miles in \(\frac{1}{3}\) hour. Jenn runs 5 miles in \(\frac{3}{4}\) hour.
1 hour = 60 mins
Jana: 1/3 hour = 1/3 × 60 = 20 minutes
Jana = Time/Distance = 20/3 = 16.7 min/mile
Jenn runs 5 miles in \(\frac{3}{4}\) hour
Jenn: 3/4 hour = 3/4 × 60 = 45 min
Jenn = Time/Distance = 45/5 = 9 min/miles
Jenn runs faster at 9 min/mile
Unit Rate
Jana = 16.7 min/mile
Jenn = 9min/mile
Question 8.
A scale drawing of a rectangular mural has the dimensions 2 inches by 3 inches. The scale is 0.5 inches:5 feet. Find the actual dimensions of the mural. Then find the dimensions of another scale drawing with the scale 0.25 inches:10 feet. ________
Answer:
Given,
A scale drawing of a rectangular mural has the dimensions 2 inches by 3 inches.
The scale is 0.5 inches:5 feet.
2 ÷ (0.5:5) = 20 feet
3 ÷ (0.5:5) = 30 feet
20 × (0.25:10) = 0.5 in
30 × (0.25:10) = 0.75 in.
Question 9.
Write an equation of the form y = kx for the relationship shown in the graph or table.
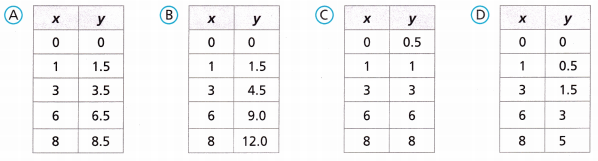
Answer:
Write an equation of the form y = kx for the relationship shown in the graph or table.
Question 10.
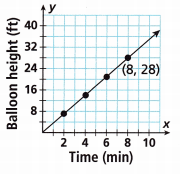
__________
Answer:
(2, 8), (4, 12), (6, 16)
Question 11.

Answer:
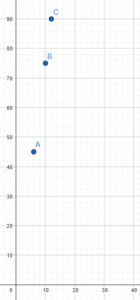
Question 12.
Use the graph from Problem 10. What is the value of r at the point with coordinates (1, r)? What does this point mean in terms of the proportional relationship shown in the graph?
________________________
________________________
Answer:
Question 13.
A store sells beans for 80tf per pound.
A. Graph the proportional relationship that gives the cost y in dollars of buying x pounds of beans.
________________________
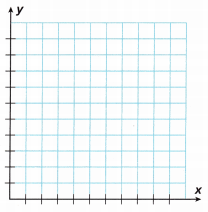
Answer:
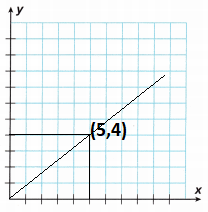
B. Write an equation of the form y = kx to represent this relationship.
________________________
Answer: y = 0.8x
C. A farmers’ market sells organic locally grown beans for $1.25 per pound. How much more would it cost to buy 3 pounds of beans at the farmers’ market than at the store?
________________________
Answer:
3 × 1.25 – 3 × 0.8
3.75 – 2.4 = 1.35