We included HMH Into Math Grade 7 Answer Key PDF Module 1 Lesson 5 Use Proportional Relationships to Solve Rate Problems to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Lesson 5 Answer Key Use Proportional Relationships to Solve Rate Problems
I Can identify the constant of proportionality and write an equation for a proportional relationship presented in various forms and use them to solve multistep ratio problems.
Step it Out
1. The bar diagram shows how many inches a garden snail travels over time. At this rate, how many feet would the snail travel in 0.75 hour?
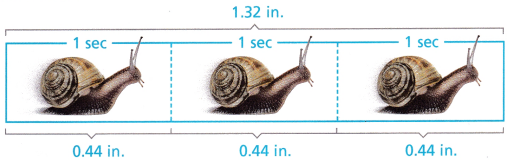
A. What is the unit rate in inches per second? Use conversion factors to convert the unit rate to feet per hour.

Answer:
Given that,
The snail travel per second is 0.44 in.

B. Write an equation for the number of feet y the snail travels in x hours, and use it to solve the problem.
y = kx
y = ____x
y = ___ (____) = 99 feet in 0.75 hour
Answer:
y = Kx
y = 0.75 x
y = 0.75 x 132 = 99 feet’s
The snail travel in 0.75 hours is 99 feet.
C. What is the unit rate in miles per hour? Write an equation for the number of miles y the garden snail travels in x hours. (5,280 ft = 1 mi)

Answer:
1 mile = 5280 ft
0.025 mile = 132 feet
y = 132x
Turn and Talk Explain how you converted the unit rate to miles per hour.
2. The graph shows the number of gallons of water used over time in one lane of a car wash. At this rate,
how much water would be used if the lane were used continuously from 8:00 a.m. to noon?
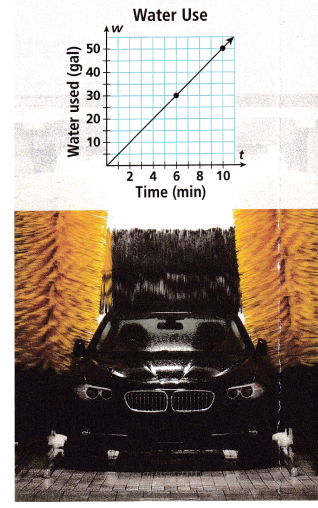
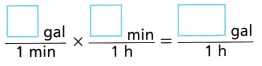
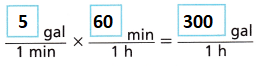
A. What is the unit rate in gallons per minute? Use conversion factors to convert the unit rate to gallons per hour.
Answer:
B. Use the graph to determine who is earning a greater rate of pay. Explain how you know.
y = kx
y = ___x
y = ___ (____) = 1,200 gallons
Answer:
(6, 30)
y = kx
30 = 6k
k = 5
y = 5x
If y = 1200
1200 = 5x
x = 1200/5
x = 240
y = 5(240) = 1200 gallons
C. How much water would be used during
the hours of 7:30 a.m. to 3:45 p.m.?
y = ____x
y = ( ) 2,475 gallons
Answer:
y = 5x
2475 = 5x
x = 2475/5
x = 495
y = 5x
y = 5(495) = 2475 gallons
Turn and Talk In Parts B and C, how did you find the number to put in the parentheses?
3. The graph shows Michaela’s earnings over time. Marcus’s hourly rate is represented in the table. Who has a greater rate of pay, and how much more than the other will that person earn in 40 hours of work?
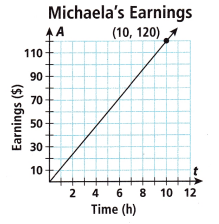

A. Complete the table, write an equation, and graph Marcus’s earnings A over time t.
k = \(\frac{19}{2}\) = ___ A = ___
B. Use the graph to determine who is earning a greater rate of pay. Explain how you know.
____________________
____________________
C. What information do you still need in order to solve the problem? Solve the problem and show your work.
I still need: ____________________
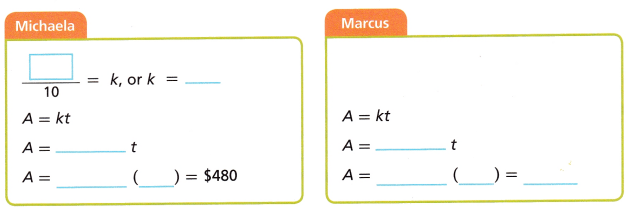
Turn and Talk What happens to the difference in their earnings over time?
Check Understanding
Question 1.
Solve the problems using the diagrams.
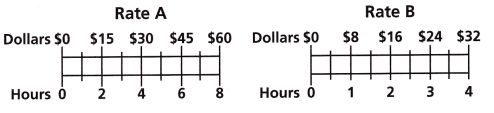
A. Write an equation for the number of dollars y earned from working x hours for each rate.
_____________________
Answer:
The equation for the number of dollars y earned from working x hours is k = y/x
For Rate A
0/0 = 0
$15/2 = $7.5
$30/4 = $7.5
$45/6 = $7.5
$60/8 = $7.5
k = 7.5
There the equation is y = Kx.
The equation is y = 7.5x
If x = 0 then y = 7.5(0) = $0
If x = 2 then y = 7.5(2) = $15
If x = 4 then y = 7.5(4) = $30
If x = 6 then y = 7.5(6) = $45
If x = 8 then y = 7.5(8) = $60
For Rate B
0/0 =0
$8/1 = $8
$16/2 = $8
$24/3 = $8
$32/4 = $8
Therefore the equation is y = Kx
If x = 0 then y = 8(0) = $0
If x = 1 then y = 8(1) = $8
If x = 2 then y = 8(2) = $16
If x = 3 then y = 8(3) = $24
If x = 4 then y = 8(4) = $32
For the Rate A k = 7.5
For the rate B k = 8
B. What is the difference between total dollars earned from 40 hours of work for these rates? Show your work.
_____________________
Answer:
For Rate A, the total dollars earn for 40 hours is 7.5(40) = $300.
For Rate B the total dollars earned for 40 hours is 8(40) = $320.
The difference between total dollars earned from 40 hours of work for these rates is $20.
On Your Own
Question 2.
Use the diagram of distance traveled at a constant rate.
A. What is the unit rate?
_____________
Answer:
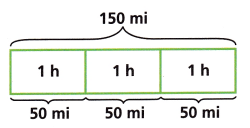
B. Convert the rate to feet per minute.
_____________
Answer:
C. Convert the rate to inches per second.
_____________
Answer:
Question 3.
Model with Mathematics The graph shows the number of cubic feet of water used over time at a water park that is open during the hours in the table. At this rate, how many cubic feet of water would be used at the water park on a Sunday?

A. What is the unit rate in cubic feet per minute?
______________________
Answer:
Given that the time is 1 min
The water used in feet is 30 cubic feet.
Divide cubic feet by minute
30/1 = 30.
The time is 5 min
The water used in feet is 150 cubic feet.
150/3 = 30
Therefore the unit rate is 30 cubic feet per minute
B. What is the unit rate in cubic feet per hour?
______________________
Answer:
Given that the time is 1 hour
The water used in feet is 30 cubic feet.
Divide cubic feet by the hour
30/1 = 30cubic feet/hour.
The unit rate is 30 cubic feet/hour.
C. Write an equation for the number of cubic feet of water y used in x hours, and use it to solve the problem.
______________________
Answer:
The equation is k = y/x
Divide feet/hours
30/1 = 30
150/3 = 30
The value of k is 30cubic feet/hours.
D. How many cubic feet of water would be used at the water park on a Tuesday?
______________________
Answer:
Given that,
The water park operation on Tuesday is 11 am to 7.30 pm
The number of hours is 8.5 hours.
1 hour = 30 cubic feet of water.
For 8.5 hours = 8.5 x 30 = 255 cubic feet/hours.
Therefore 255cubic feet of water would be used at the water park on a Tuesday.
Question 4.
Model with Mathematics The distance Dan jogged over time is shown in the graph. Pattie’s constant jogging speed is represented in the table. Who has a faster jogging speed? How much more distance will that jogger have traveled with a total of 22 hours jogging?
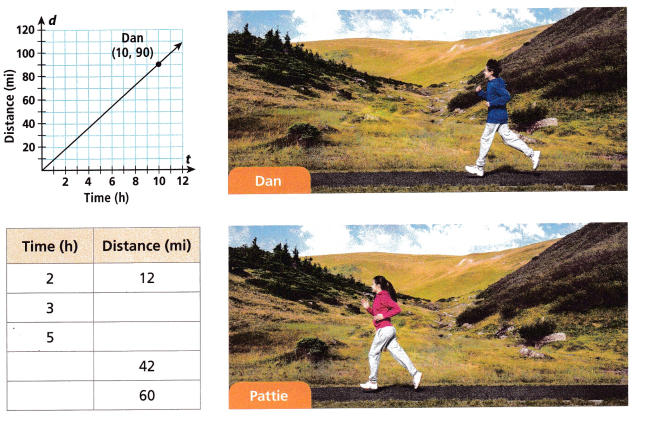
A. Use the table to find Pattie’s jogging speed k. Complete the table.
______________________
Answer:
The equation is y = Kx
y = 6x
If x = 2 then y = 6(2) = 12
If x = 3 then y = 6(3) = 18
If x = 5 then y = 6(5) = 30
If x = 7 then y = 6(7) = 42
If x = 10 then y = 6(10) = 60
The constant proportionality k is 6
B. Write an equation for the distance in miles d that Pattie jogs in t hours. Graph the equation on the grid with Dan’s graph.
______________________
Answer:
Plot the points (2,12), (3,18), (5,30), (7,42), (10,60) on the Dan plot.
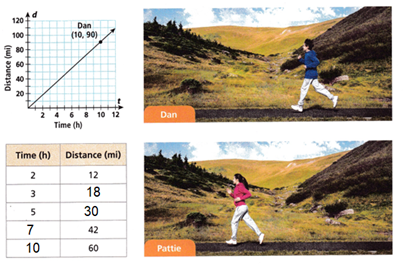
C. Solve the problem and show your work.
______________________
Answer:
The equation is y = Kx
y = 6x
If x = 2 then y = 6(2) = 12
If x = 3 then y = 6(3) = 18
If x = 5 then y = 6(5) = 30
If x = 7 then y = 6(7) = 42
If x = 10 then y = 6(10) = 60
The Pattie jog for 22 hours = 132 miles.
The constant proportionality is 6.
From the graph the Dan is running fast.
Question 5.
A cheetah, the world’s fastest land animal, cannot maintain its top speed for very long. This bar diagram shows a cheetah’s top speed, in feet per minute. Suppose a racecar is driven at the cheetah’s top speed. How many miles would it travel in 3 hours?
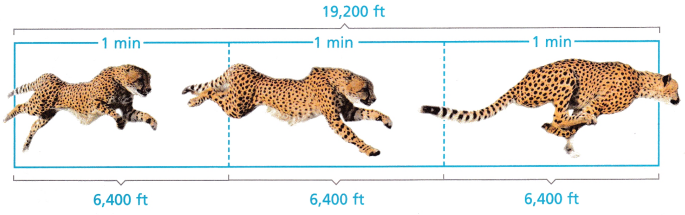
A. What is the unit rate in feet pet hour?
_____________________
Answer:
B. What is the unit rate in miles per hour, to the nearest tenth?
_____________________
Answer:
C. Write an equation for the number of miles y that the racecar travels in x hours, and use it to solve the problem.
_____________________
Answer:
Question 6.
Rhoni reads at a rate of 75 pages per hour. The number of pages Rie reads over time is shown in the table.

A. Who has a greater rate of reading?
_____________________
Answer:
Given that,
Rhoni reads at a rate of 75 pages per hour.
Rie reading rate is
195/3 = 65
325/5 = 65
585/9 = 65
650/10 = 65
Rie reads at the rate of 65 pages per hour.
Therefore Rhoni has the greater rate of reading.
B. At these rates, what is the difference in the number of pages they will read in 4 hours?
_____________________
Answer:
Rhoni reads at a rate of 75 pages per hour.
For 4 hours = 74 x 4 = 300 pages
Rie reads at the rate of 65 pages per hour.
For 4 hours = 65 x 4 = 260 pages.
The difference is 300 – 260 = 40 pages.
Therefore 40 pages are different in the number of pages they will read in 4 hours
C. How long will it take each student to read a book with 780 pages? Show your work.
_____________________
_____________________
Answer:
Rhoni reads at a rate of 75 pages per hour.
Rie reads at the rate of 65 pages per hour.
For 780 pages the Rhoni reads is 780/75 = 10.4 which means 10 hours 4 min.
Rhoni takes 10 hours and 4 min to read 780 pages of book.
For 780 pages the Rie reads is 780/65 = 12 hours.
Rie takes 12 hours to read 780 pages of book.
Lesson 1.5 More Practice/Homework
Give each rate in miles per hour. Round to the nearest tenth.
Question 1.
Dey jogs 8\(\frac{1}{2}\) miles in 1\(\frac{1}{2}\) hours.
Answer:
Given that,
8\(\frac {1}{2} \) miles = 8 x 1/2 miles.
1\(\frac {1}{2} \) hours = 1 x 1/2 hours.
Divide miles by hours
8 x 1/2 ÷ 1 x 1/2
= 4/0.5
= 8 miles per hour.
The unit is 8 miles per hour.
8 rounded to the nearest tenth is 10.
Question 2.
Caroline walks 9\(\frac{1}{2}\) inches per second.
_____________
Answer:
Given that,
9\(\frac {1}{2} \) = 9 x 1/2 inches. = 4.5 inches.
4.5 inches in miles = 0.00007102
1 second in miles = 0.000278 hours
Divide miles/hours
0.00007102/0.000278
= 0.255 miles/hour
The unit rate is 0.255 miles/hour
0.255 rounded to the nearest tenth is 0.
Question 3.
Dhruv jogs 8 feet per second.
_____________
Answer:
Given that,
8 feet in miles is 0.0015 miles
1 second in hours is 0.000278 hours
Divide miles/hours
0.0015/0.000278 = 5.39
The unit rate is 5.39 miles/hour
5.39 rounded to the nearest tenth is 10.
Question 4.
Rachel jogs 20 feet in 3 seconds.
_____________
Answer:
Given that,
20 feet in 3 seconds
20 feet = 0.00378 miles
3 seconds in hours is 0.000833 hours
Divide miles by hours
0.00378/0.000833 = 4.53miles/hour
The unit rate is 4.53miles/hour
4.53 rounded to the nearest tenth is 0.
Question 5.
A bald eagle flies 43.2 meters in 3 seconds. The graph shows the distance a typical peregrine falcon flies over time. At these rates, what is the difference in the distances flown by these two birds after 3 hours of flight? Show your work.

Answer:
Given,
A bald eagle flies 43.2 meters in 3 seconds.
v1 = 400/5 = 80 km/hr
v2 = 43.2/3 = 14.4 m/s
14.4 m/s = (14.4 ÷ 1000)/(1 ÷ 3600) km/h
= 14.4 × 3.6 = 51.84 km/hr
The distance between the two birds after 3 hours
s = (v1 – v2)t
s = (80 – 51.84) × 3
s = 84.48 km
Question 6.
Two water tanks are leaking. Tank A has leaked \(\frac{1}{16}\) of a gallon in \(\frac{1}{12}\) minute, and Tank B has leaked \(\frac{3}{80}\) of a gallon in \(\frac{1}{30}\) minute. Which tank is leaking faster?
_____________
Answer:
Given that,
Tank A has leaked \(\frac{1}{16} \) of a gallon in \(\frac{1}{12}\) minute
\(\frac{1}{16}\) = 1/6 gallon.
\(\frac{1}{12}\) = 1/12 minutes.
Tank B has leaked \(\frac{3}{80}\) of a gallon in \(\frac{1}{30}\) minute.
\(\frac{3}{80}\) = 3/80 gallon
\(\frac{1}{30}\) = 1/30 minutes.
Therefore the ratio of gallons and minutes is
Tank A = 1/6 ÷ 1/12 = 2 gallons/minute.
Tank B = 3/80 ÷ 1/30 = 1.125 gallons/minute
Therefore Tank A is leaking faster.
Question 7.
Model with Mathematics Write an equation for each boat- rental company that gives the cost in dollars y of renting a kayak for x hours. What is the difference in cost between the company that charges the most and the one that charges the least for 4 hours? Show your work.
Company B The cost y of renting a kayak for x hours is $9.00 for each half hour.
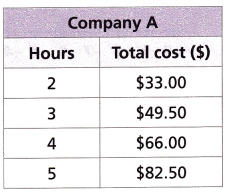
Company C The cost y of renting a kayak is $14.25 per hour.
______________________
______________________
______________________
Answer:
Company A: y = 33 + 16.5(x – 2)
Company B: $9 for each half an hour
So there are $18 for each hour
9 × 2 = $18
y = 18x
Company C: y = 14.25x
When x = 4 hours
Company A: y 33 + 16.5(x – 2) = 33 + 16.5 0215 2 = 66
Company B: y = 18x = 18 × 4 = 72
Company C: y = 14.25 × 4 = 57
So, the difference in cost between the most and the least company is 72 – 57 = $15
Test Prep
Question 8.
James walked at a constant rate for 3 hours as shown in the graph. Jaycee walked 14.5 miles in 3 hours at a constant rate. Who walked farther, and how much farther? Explain.
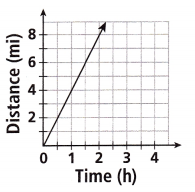
______________________
______________________
______________________
Answer:
Given that,
James walked at a constant rate for 3 hours.
Jaycee walked 14.5 miles in 3 hours at a constant rate.
From the given graph the equation is y= 4x
Substitute x = 3 in the above equation.
then y = 4(3) = 12.
James walked 12 miles in 3 hours.
Therefore 14.5 – 12 = 2.5
Therefore Jaycee walked 2.5 miles faster than the James.
Question 9.
A squirrel can run a short distance at a rate of 4\(\frac{3}{4}\) miles in 15 minutes. A fox can run a short distance at a rate of 21 miles in half an hour. Which is faster, and how much faster in miles per hour?
A. the squirrel; 23 miles per hour
B. the fox; 23 miles per hour
C. the squirrel; 2 miles per hour
D. the fox; 2 miles per hour
Answer: B. the fox; 23 miles per hour
Question 10.
Joelle can read 3 pages in 4 minutes, 4.5 pages in 6 minutes, and 6 pages in 8 minutes. Paxton can read 3 times as fast as Joelle. Which is the equation for the number of pages y that Paxton can read in x minutes?
A. y = \(\frac{9}{4}\)x
B. y = \(\frac{6}{5}\)x
C. y = \(\frac{3}{4}\)x
D. y = \(\frac{1}{4}\)x
Answer:
Given that,
Joelle can read 3 pages in 4 minutes
Paxton can read 3 times as fast as Joelle
Therefore Paxton reads 3 x 3 = 9 and 4 x 3 = 12
The ratio of pages by minutes is 9/12 = 3/4.
Therefore the answer is y = \(\frac {3}{4} \)x
Option C is the correct answer.
Spiral Review
Compare. Write < or >.
Question 13.
List the numbers in order from least to greatest.
-2, 8, -15, -5, 3, 1
_____________
Answer:
The numbers from least to greatest is
-15, -5, -2, 8, 3, 1
Graph each number on the number line. Then use your number line to find the absolute value of each number.

Question 14.
2 ____
Answer:
The absolute value is always positive.
To find the absolute value of a negative number just remove the negative sign.
The absolute value of 2 is 2

Question 15.
-8 ____
Answer:
The absolute value is always positive.
To find the absolute value of a negative number just remove the negative sign.
The absolute value of -8 is 8

Question 16.
-5 ____
Answer:
The absolute value is always positive.
To find the absolute value of negative number just remove the negative sign.
The absolute value of -5 is 5
