We included HMH Into Math Grade 7 Answer Key PDF Module 1 Lesson 3 Compute Unit Rates Involving Fractions to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Lesson 3 Answer Key Compute Unit Rates Involving Fractions
I Can compute unit rates associated with ratios of fractions.
Spark Your Learning
Rick and Tina hiked at different constant rates. Rick hiked \(\frac{1}{2}\) mile every 15 minutes, or \(\frac{1}{4}\) hour. It took Tina 10 minutes to hike \(\frac{1}{4}\) mile. Find the distance each hiked in 1 hour.


Turn and Talk How can you use the distance they each hiked in 1 hour to write a ratio for the distance they each would hike in 2 hours?
Build Understanding
1. Jessie loves to go hiking on rustic trails through trees and along rivers. One day in 20 minutes of hiking, she hiked 1 mile. If Jessie hiked at a constant rate, what would that rate be?
A. Write Jessie’s hiking rate in all the ways you can think of from the information given.
Answer:
One day in 20 minutes of hiking, she hiked 1 mile.
The one way is
The Jessie hiked at a constant rate is 20/1 minutes/mile.
Another way is
1/20 miles/minute.
= 1/mile/1/3 hours
= 1 x 3/1 ÷ 1/3 x 3/1 = 3miles/hour.
B. Complete the statements below to show how to write Jessie’s hiking rate as a unit rate in miles per hour.

You have to multiply \(\frac{1}{3}\) hour by ___ to make the second quantity in the unit rate ____ hour, so multiply the first quantity by _____ as well.
Answer:
1 mile/20 minutes = 1 mile/\(\frac{1}{3}\) hour = 1 mile/\(\frac{1}{3}\) hour × 3/3 = 3 miles/1 hour
You have to multiply \(\frac {1}{3} \) hour by 3/1 mile to make the second quantity in the unit rate 1/3 hour, so multiply the first quantity by 3/1 as well.
C. Amiya prefers hiking on more hilly trails. One time Amiya reached the mile marker pictured in 20 minutes hiking at a steady pace. Show how to find the unit rate in minutes per mile.


Answer:
Given that,
One time Amiya reached the mile marker pictured in 20 minutes hiking at a steady pace.
The unit rate in minutes per mile is 20 min/mile
Turn and Talk Compare the rates “minutes per mile” and “miles per minute.” Give an example of each rate.
Answer:
The ratio of minutes per mile = 20/1 = 20 miles per hour.
The ratio of miles per hour = 1/20 hours/mile.
Step It Out
2. A recipe says to use \(\frac{2}{3}\) cup of milk to make \(\frac{4}{5}\) serving of pudding. How many cups of milk are in 1 serving?
A. Recall that reciprocals are two numbers whose product is 1. Explain how reciprocals are used to find the unit rate.

____________________
____________________
Answer:
The reciprocals are 4/5 x 5/4 = 1
To find the unit rate the denominator is always 1.
So, will using the reciprocals the denominator becomes 1.
B. How can you use division to find this unit rate?
____________________
Answer:
For the unite rate divide the denominator with numerator then the denominator becomes 0.
Turn and Talk How can you find the number of servings of pudding for every cup of milk?
3. Jaylan makes limeade using \(\frac{3}{4}\) cup of water for every \(\frac{1}{5}\) cup of lime juice. Rene’s limeade recipe is different. He uses \(\frac{2}{3}\) cup of water for every \(\frac{1}{6}\) cup of lime juice. Whose limeade has a weaker flavor?
A. What do you need to know to solve this problem?
____________________
Answer:
Solve the unit rate of water to the lime juice in each limeade.
B. Compute the unit rate of water to lime juice in each limeade.
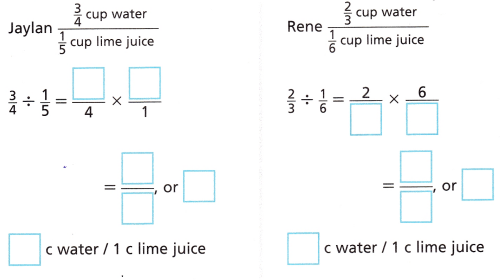
Answer:
Given that,
Jaylan makes limeade using \(\frac {3}{4} \) cup of water for every \(\frac {1}{5} \) cup of lime juice.
\(\frac {3}{4} \) = 3/4
\(\frac {1}{5} \) = 1/5
Rene’s limeade recipe is different. He uses \(\frac {2}{3} \) cup of water for every \(\frac {1}{6} \) cup of lime juice.
\(\frac {2}{3} \) = 2/3
\(\frac {1}{6} \) = 1/6
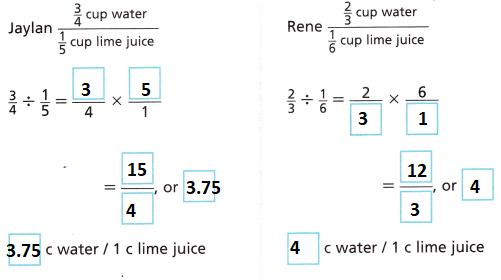
C. Whose limeade has a weaker flavor? Explain.

____________________
____________________
Answer:
The Jaylan limeade is 3.75 c water per 1 c lime juice.
The Rene Limeade is 4 c water per 1 c lime juice.
Therefore Jaylan Limeade is a weaker flavor than the Rene limeade.
4. The moon has a weaker gravitational pull than Earth, so objects weigh less on the moon. For example, Jaxon weighs 30\(\frac{5}{6}\) pounds on the moon and 185 pounds on Earth. Viola weighs 135 pounds on Earth and 22\(\frac{1}{2}\) pounds on the moon.
A. Show that the relationship between weight on the moon and weight on Earth is proportional.
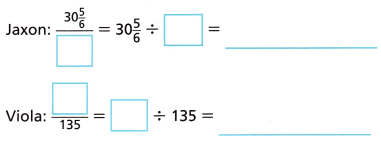
The constant of proportionality for ![]() is _________
is _________
Answer:
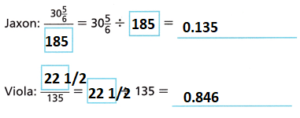
The constant of proportionality for moon weight/earth weight = 0.135/0.846 = 0.159 lb.
B. Let x represent the weight on Earth. Let y represent the weight on the moon. Write an equation for the proportional relationship. Use it to find the weight of a 20-pound dog on the moon.
The equation is _____.
On the moon, the dog would weigh about ____ pounds.
Answer:
Given that,
x represents the earth
y represents the moon
The equation for the proportional relationship is = x/y.
The weight of the moon is the 20-pound dog.
Therefore the equation is x/20.
On the moon, the dog would weigh about x/20 pounds
Turn and Talk What would a dog that weighs 12 pounds on the moon weigh on Earth?
Check Understanding
Question 1.
A faucet leaks \(\frac{5}{8}\) quart of water in 15 minutes. How many quarts does the faucet leak per hour?

____________________
Answer:
Given that,
A faucet leaks \(\frac {5}{8} \) quart of water in 15 minutes.
\(\frac {5}{8} \) quart of water = 5/8 quart of water.
1 hour = 60 minutes
60/15 = 4
In 1 hour there are 4 quart = 5/8 x 4 = 2.5
In 4 quarts the faucet leak 2.5 of water per hour.
Question 2.
Toni ran \(\frac{4}{5}\) mile in \(\frac{1}{5}\) hour. Write an equation for the distance in miles y that she ran in x hours if she ran at a constant rate.
Answer:
Given that,
Toni ran \(\frac {4}{5} \) mile = 4/5 mile.
Toni ran in hours = \(\frac {1}{5} \) = 1/5 hours
The equation for the distance in miles y that she ran in x hours is
y/x = 4/5 ÷ 1/5
y/x = 0.8 ÷ 0.2
y/x = 0.4
The constant rate is 0.4 miles/hour.
Question 3.
Write \(\frac{3}{4}\) cup per \(\frac{1}{2}\) serving as a unit rate.

Answer:
Given that,
\(\frac {3}{4} \) cup = 3/4 cup.
\(\frac {1}{2} \) serving = 1/2 serving.
Divide the cup by serving.
3/4 ÷ 1/2
= 1.5
The unit rate is 1.5 cups/serving.
Question 4.
Write 2\(\frac{1}{4}\) miles in \(\frac{3}{4}\) hour as a unit rate.
Answer:
Given that,
2\(\frac {1}{4} \) miles = 2 x 1/4 miles.
\(\frac {3}{4} \) hour = 3/4 hours.
Know divide miles by hours
2 x 1/4 ÷ 3/4
= 0.5 ÷ 0.75
= 0.66 miles/hours.
The unit rate is 0.66 miles/hour.
On Your Own
Question 5.
Health and Fitness Jorge measured his heart rate after jogging. He counted 11 beats during a 6-second interval. What was the unit rate for Jorge’s heart rate in beats per minute? _________
Answer:
Given that,
Jorge measured his heart rate after jogging.
He counted 11 beats during a 6-second interval.
The unit rate for Jorge’s heart rate in beats per minute is
Divide beats by hours.
11/6 = beats/minute
The unit rate for Jorge’s heart rate in beats per minute is 1.83.
Question 6.
Chen bikes 2\(\frac{1}{2}\) miles in \(\frac{5}{12}\) hour, What is Chen’s unit rate in miles per hour?
____________________
Answer:
Given that,
2\(\frac {1}{2} \) miles = 2 x 1/2 miles.
\(\frac {5}{12} \) hour = 5/12 hours
Know divide miles by hours.
2 x 1/2 ÷ 5/12
= 1 ÷ 0.416
= 2.403 miles/hours.
The unit rate is 2.403 miles/hour.
Question 7.
Amal can run \(\frac{1}{8}\) mile in 1\(\frac{1}{2}\) minutes.
A. If he can maintain that pace, how long will it take him to run 1 mile?
_____________________
Answer:
Amal run \(\frac{1}{8}\) mile in 1\(\frac{1}{2}\) minutes.
1\(\frac{1}{2}\) = 1.5
1.5 × 8 = 12 minute
B. How long would it would take Amal to run 3 miles at that pace?
_____________________
Answer: It would also take him 12 minutes.
C. Naomi can run \(\frac{1}{4}\) mile in 2 minutes. Does Amal or Naomi run faster? How do you know?
_____________________
Answer:
Given,
Amal can run \(\frac{1}{8}\) mile in 1\(\frac{1}{2}\) minutes.
\(\frac{1}{8}\) ÷ 1\(\frac{1}{2}\)
Convert from mixed fraction to the improper fraction
\(\frac{1}{8}\) ÷ \(\frac{3}{2}\) = \(\frac{1}{12}\) mile/minute
Naomi can run \(\frac{1}{4}\) mile in 2 minutes.
\(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\) mile/minute
Thus Naomi runs faster than Amal.
Question 8.
Open Ended When both quantities in a rate are fractions, what strategy do you use to write the rate as a unit rate?
________________________
________________________
Answer:
When both quantities in a rate are fractions, the strategy is.
First, write the ratios as the fraction and divide the numerator by the denominator.
Question 9.
Reason What is the ratio of dried fruit to sunflower seeds in the granola recipe? If you need to triple the recipe, will the ratio change? Explain.
________________________
________________________

Answer:
Given that,
Dried fruit = 1/2 cup.
Sunflower seeds = 1/8 cup.
The ratio of dried fruit to sunflower seeds in the granola recipe is 1/2 ÷ 1/8 = 4 cups
Triple the recipe = 4 x 4 x 4 = 64 cups.
Yes, when you triple the recipe the ratio will change.
Question 10.
The table shows the numbers of packages of peanut butter crackers y that can be made using various amounts of peanut butter x.

A. Show that the relationship is proportional.
_____________
Answer:
Yes, the relationship is proportional.
The equation is y = 4x.
B. Write an equation to represent the relationship, and find the amount of peanut butter used to make 25 cracker packages.
_____________
Answer:
The equation to represent the relationship y = 4x
Here, m = 4.
Find the amount of peanut butter used to make 25 cracker packages is
25 = 4x
x = 25/4
Therefore You need to use 25/4 teaspoons of peanut butter used to make the 25 cracker packages.
Question 11.
The relationship between adult dog weight x in pounds and the daily recommended amount of dog food y in cups is proportional.

Write an equation for the relationship. How much dog food is recommended for a 25-pound adult dog?

Answer:
Given that,
Food for the 50 pounds of the dog = 5/6 cups.
50 pounds = 50/2 = 25 pounds.
For 25 pounds of dog = 5/6 ÷ 2 = 5/12 cups.
The dog food recommended for a 25-pound adult dog is 5/12 cups.
For Exercises 12—15, find each unit rate.
Question 12.
\(\frac{5}{8}\) mile in \(\frac{1}{4}\) hour
Answer:
Given that,
\(\frac {5}{8} \) mile = 5/8 mile.
\(\frac {1}{4} \) hour = 1/4 hour.
Divide mile by hour.
5/8 ÷ 1/4
= 2.5 mile/hour
The unit rate is 2.5 miles/hour.
Question 13.
$68 for 8\(\frac{1}{2}\) hours
Answer:
Given that,
$68 for 8\(\frac {1}{2} \) hours
$68 for 8 x 1/2.
Divide dollars by hours.
68 ÷ 1/2
68 ÷ 0.5
= 136 dollars/hours.
The unit rate is 136 dollars/hour.
Question 14.
1\(\frac{1}{4}\) cup of flour per \(\frac{1}{8}\) cup of butter
Answer:
Given that.
1\(\frac {1}{4} \) cup of flour = 1 x 1/4
\(\frac {1}{8} \) cup of butter = 1/8
Know to divide a cup of flour with a cup of butter.
1 x 1/4 ÷ 1/8
= 0.25 ÷ 0.125
= 0.25 ÷ 0.125
= 2 cups of flour/cups of butter.
The unit rate is 2 cups of flour/cups of butter.
Question 15.
2\(\frac{1}{2}\) miles in \(\frac{3}{4}\) hour
____________________
Answer:
Given that,
2\(\frac {1}{2} \) miles = 2 x 1/2.
\(\frac {3}{4} \) hour = 3/4.
Divide miles by hours.
2 x 1/2 ÷ 3/4
= 1 ÷ 0.75
= 1.33 miles/hour.
The unit rate is 1.33 miles/hour.
I’m in a Learning Mindset!
What did I learn from peers when they shared their strategies with me for writing a unit rate?
Lesson 1.3 More Practice/Homework
Compute Unit Rates Involving Fractions
Question 1.
STEM Density is a unit rate measured in units of mass per unit of volume. The mass of a garnet is 5.7 grams. The volume is 1.5 cubic centimeters (cm3). What is the density of the garnet?
Answer:
Given that,
The mass of the garnet is 5.7 grams.
The volume is 1.5 cubic centimetres.
The formula for the density is mass/volume.
The density of the grant is 5.7 grams/1.5 cubic centimeters.
The density of the grant = 3.8 grams/cubic centimeters.
Question 2.
Math on the Spot Jen and Kamlee are walking to school. After 20 minutes, Jen has walked \(\frac{4}{5}\) mile. After 25 minutes1 Kamlee has walked \(\frac{5}{6}\) mile. Find their speeds in miles per hour. Who is walking faster?
Answer:
Given that,
Jen and Kamlee are walking to school.
After 20 minutes, Jen has walked \(\frac{4}{5}\) mile.
\(\frac{4}{5}\) mile = 4/5 mile.
After 25 minutes1 Kamlee has walked \(\frac{5}{6}\) mile.
\(\frac{5}{6}\) = 5/6 mile.
The formula for the speed = distance/time
1 hour = 60 minutes.
The speed of Jan = 4/5 ÷ 20/60
= 12/5
= 2.4 miles per hour.
The speed of Kamlee = 5/6 ÷ 25/60
= 2 miles per hour.
Therefore Jan is 2.4 miles per hour and Kamlee is 2 hours per hour. So, Jan is walking faster.
Question 3.
Reason Maria and Franco are mixing sports drinks for a track meet. Maria uses \(\frac{2}{3}\) cup of powdered mix for every 2 gallons of water. Franco uses 1\(\frac{1}{4}\) cups of powdered mix for every 5 gallons of water. Whose sports drink is stronger? Explain how you found your answer.
________________________
________________________
________________________
Answer:
Given that,
Maria uses \(\frac{2}{3}\) cup of powdered mix for every 2 gallons of water.
\(\frac{2}{3}\) cup of powdered mix = 2/3.
Franco uses 1\(\frac{1}{4}\) cups of powdered mix for every 5 gallons of water.
1\(\frac{1}{4}\) cups of powdered mix = 1 x 1/4.
For maria the ratio of the powered mix to the water is
2/3 ÷ 2
= 1/3 cup/gallon
For Franco the ratio of the powered mix to the water is
1 x 1/4 ÷ 5
= 5/4 ÷ 5
= 1/4 cup/gallon
The 1/3 is bigger than the 1/4. So, Mria’s sports drink is stronger than the Franco sports drink.
Question 4.
Model with Mathematics Serena estimates that she can paint 60 square feet of wall space every half-hour. Write an equation for the relationship with time in hours as the independent variable. Can Serena paint 400 square feet of wall space in 3.5 hours? Why or why not?
________________________
Answer:
Given that,
Serena can paint = 60 square feet.
The time taken to paint = half-hour = 0.5 hours.
0.5 hours = 60 square feet’s.
For 1 hour = 60/0.5 = 120 sq. feet’s.
For I hours = 120i sq. feet’s.
Let us consider that the total area is y.
The relation between the I hours to the independent variable is
y = 120I
Can Serena paint 400 square feet of wall space in 3.5 hours?
Put y = 400 and I = 3.5 then
400 = 120(3.5)
400 is not equal to 420.
Therefore Serena cannot paint 400 square feet in 3.5 hours.
Question 5.
Cheri paid $6.50 for the bunch of grapes with the weight shown on the scale. What was the price per pound?
________________________

Answer:
Given that,
The cost for the bunch of graphs = $6.50
The weight of the grapes = 5 lb
Divide price by pound.
$6.50 ÷ 5
= 1.3
The unit rate is 1.3 price/lb
Find the unit rate.
Question 6.
\(\frac{1}{4}\) kilometer in \(\frac{1}{3}\) hour
Answer:
Given that,
\(\frac {1}{4} \) kilometre = 1/4 kilometre.
\(\frac {1}{3} \) hour = 1/3 hour
Divide the kilometre by hours
The unit rate is 1/4 ÷ 1/3 = 3/4 = 0.75 kilometre/hour.
Question 7.
\(\frac{7}{8}\) square foot in \(\frac{1}{4}\) hour
Answer:
Given that,
\(\frac {7}{8} \) square foot = 7/8 square foot.
\(\frac {1}{4} \) hour = 1/4 hour
Divide the square foot by the hour.
The unit rate is 7/8 ÷ 1/4 = 3.5 square feet/hour.
Question 8.
$6.50 for 3\(\frac{1}{4}\) pounds of grapes
Answer:
Given that,
Cost of the graphs = $6.50
The weight of the graphs = 3\(\frac {1}{4} \) pounds = 3 x 1/4 pounds.
Divide dollar by pounds.
The unit rate is $6.50 ÷ 3 x 1/4
= $6.50 ÷ 0.75
= 8.6 dollar/pounds
Question 9.
$49.50 for 5\(\frac{1}{2}\) hours
Answer:
Given that,
$49.50 for 5\(\frac {1}{2} \) hours.
$49.50 for 5 x 1/2 hours.
Divide dollar by hours
$49.50 ÷ 5 x 1/2
$49.50 ÷ 2.5
= 19.8
The unit rate is 19.8 dollars/hour.
Question 10.
247 heart beats in 6\(\frac{1}{2}\) minutes
Answer:
Given that,
247 heartbeats in 6\(\frac {1}{2} \) minutes.
247 heartbeats in 6 x 1/2.
Divide heartbeats by minutes.
247 ÷ 6 x 1/2
= 247 ÷ 3
= 82.33 heartbeats/minutes.
The unit rate is 82.33 heartbeats/minutes.
Question 11.
8\(\frac{1}{2}\) miles in \(\frac{1}{2}\) hour
Answer:
Given that,
8\(\frac {1}{2} \) miles = 8 x 1/2.
\(\frac {1}{2} \) hour = 1/2 hour.
Know divide miles by hours.
8 x 1/2 ÷ 1/2
= 4 ÷ 0.5
= 8
The unit rate is 8 miles/hour.
Test Prep
Question 12.
Select all the rates equivalent to the rate \(\frac{3}{4}\) cup per pound.
A. \(\frac{3}{8}\) cup per \(\frac{1}{2}\) pound
B. \(\frac{1}{4}\) cup per \(\frac{1}{2}\) pound
C. 3 cups for every 2 pounds
D. 1\(\frac{1}{2}\) cups for every 2 pounds
E. 0.1875 cup for every 0.25 pound
Answer:
Question 13.
Jordan cooked a 16-\(\frac{1}{5}\)-pound turkey in 5\(\frac{2}{5}\) hours. How many minutes per pound did it take to cook the turkey? Express your answer as a unit rate.
____________________
Answer:
Given that,
Jordan cooked 16-\(\frac {1}{5} \)-pound turkey in 5\(\frac {2}{5} \) hours.
Jordan cooked 16 x 1/5-pound turkey in 5 x 2/5 hours.
16 x 1/5 = 81/5 lb.
5 x 2/5 = 27/5 hours
1 hour = 60 minutes
27/5 x 60 = 324 minutes
Know Divide the total time by the total weight.
324/81/5 = 1.620/81 = 20 min/lb
The unit rate is 20 min/lb
Question 14.
Mr. March sells popcorn at his theater. He uses 3\(\frac{3}{4}\) cups of unpopped corn to make 15 bags of popped corn. Write an equation for the number of bags of popcorn b that can be made with c cups of unpopped corn.
Answer:
Given that,
Mr. March uses 3\(\frac{3}{4}\) cups of unpopped corn to make 15 bags of popped corn.
3\(\frac{3}{4}\) cups = 3 x 3/4.
The equation for the number of bags of popcorn b that can be made with c cups of unpopped corn is b/c =
Divide bags of popped corn into cups of unpopped corn.
b/c = 15 ÷ 3 x 3/4
b/c = 15 ÷ 2.25
b/c = 6.66 bags of popped corn/cups of unpopped corn.
Question 15.
Lucia uses 3 ounces of pasta to make \(\frac{3}{4}\) serving of pasta. How many ounces of pasta are there per serving? How many ounces of pasta should Lucia use to make 5 servings?
A. 3 ounces; 15 ounces
B. 4 ounces: 20 ounces
C. 6 ounces; 30 ounces
D. 9 ounces; 40 ounces
Answer:
Given that,
Lucia uses 3 ounces of pasta to make \(\frac {3}{4} \) serving of pasta.
3 ounces of pasta to make 3/4 serving of pasta.
Divide ounces by servings.
3 ÷ 3/4
= 3 ÷ 0.75
= 4 ounces/servings
The ounces of pasta should Lucia use to make 5 servings is 4 ounces x 5.
= 20 ounces.
4 ounces: 20 ounces.
Option B is the correct answer.
Spiral Review
Question 16.
John left school with $8.43. He found a quarter on his way home and then stopped to buy an apple for $0.89. How much money did he have when he got home?
Answer:
Given that
John left the school with $8.43.
On the way home, John buys an apple for $0.89.
Therefore $8.43 – $0.89 = $7.54
John has $7.54 when he got home.
Question 17.
Arian is making bracelets. For each bracelet, it takes \(\frac{1}{10}\) hour to pick out materials and \(\frac{1}{4}\) hour to braid it together. How many bracelets can Arian make in 5 hours?
Answer:
Given that,
For each bracelet to pick out the materials = \(\frac {1}{10} \) = 1/10 hours.
For each bracelet to band it together = \(\frac {1}{4} \) = 1/4 hours.
Therefore 1/10 + 1/4 = 7/20 hours.
For 1 bracelets = 7/10 hours.
Divide available time by given time.
5 ÷ 7/20 = 14.285
Arian can make 14 bracelets in 5 hours.
Question 18.
For a game, 3 people are chosen in the first round. Each of those people chooses 3 people in the second round, and so on. How many people are chosen in the sixth round?
____________________
Answer:
In the first round, 3 people are chosen.
In the second round, these 3 people choose 3 people. It means 3 x 3 = 9
In the third round again 3 people are chosen = 9 x 3 = 27
In the fourth round again 3 people are chosen = 27 x 3 = 81
In the fifth round again 3 people are chosen = 81 x 3 = 243
In the sixth round again 3 people are chosen = 243 x 3 = 729.
The 729 people are chosen in the sixth round.