We included HMH Into Math Grade 7 Answer Key PDF Module 1 Lesson 1 Explore Relationships to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Lesson 1 Answer Key Explore Relationships
I Can recognize when relationships presented in tables, diagrams, and verbal descriptions can be represented by a constant unit rate.
Spark Your Learning
These salsas are made for a competition.

On Fire!
2 tablespoons peppers; 5 tablespoons tomatoes
Blazin’
4 tablespoons peppers; 12 tablespoons tomatoes
Kickin’
6 tablespoons peppers; 15 tablespoons tomatoes
Feel the Burn
3 tablespoons peppers; 6 tablespoons tomatoes
If peppers and tomatoes are the only ingredients in the salsaš and the names are based on taste, which two salsas should have the same name? Show your work and explain.

Turn and Talk Using the ratios described in the salsa recipes, describe which recipe is most hot and which recipe is most mild.
Build Understanding
1. The table shows how many ounces of salsa you get when buying small jars of salsa.

A. Describe a pattern you see in the rows of the table.
_________________
_________________
Answer:
The rows of small jars of salsa are increased by 4 times.
The rows of ounces of salsa are increased by 32 times.
B. Describe a pattern you see in the columns of the table.
_________________
_________________
Answer:
The pattern in the column of the table is
y = 8x
Therefore x = 4 then y = 8(4) = 32
x = 8 then y = 8(8) = 64
x = 12 then y = 8(12) = 96
x = 16 then y= 8(16) = 128.
x = 20 then y = 8(20) = 160.
C. Use your patterns to extend the table.
Answer:
The pattern in the column of the table is
y = 8x
Therefore x = 4 then y = 8(4) = 32
x = 8 then y = 8(8) = 64
x = 12 then y = 8(12) = 96
x = 16 then y= 8(16) = 128.
x = 20 then y = 8(20) = 160.

D. You previously learned that a unit rate is a rate in which the second quantity in the comparison is one unit, such as 4 ounces per 1 serving. Describe the relationship between ounces of salsa and small jars of salsa using a unit rate.
_________________
_________________
Answer:
The relationship between ounces of salsa and small jars of salsa using a unit rate is
4 ounces = 1 serving
y = 4x
If x = 1 then y = 4
If x = 2 then y = 4(2) = 8
If x = 3 then y = 4(3) = 12
If x = 4 then y = 4(4) = 16
If x = 5 then y = 4(5) = 20
E. The diagram shows how many ounces of salsa you get when buying medium jars of salsa. Describe the relationship using a unit rate.

_________________
_________________
Answer:
The relationship using the unit rate is
48 ounces = 4 medium jars of salsa.
For 1 medium jars of salsa = 48/4 = 12 ounces.
1 medium jar of salsa = 12 ounces.
Turn and Talk Is the relationship represented in the table the same as the relationship represented in the diagram in Part E? Why or why not?
2. The tables show the prices and weights of avocados.

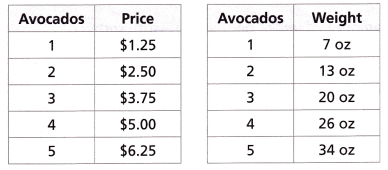
A. Can the relationship between the price and the number of avocados be described with a constant rate? Explain.
______________________
______________________
Answer:
The relationship between the price and the number of avocados is
y = 1.25x
If x = 1 then y = 1.25(1) = $1.25
If x = 2 then y = 1.25(2) = $2.50
If x = 3 then y = 1.25(3) = $3.75
If x = 4 then y = 1.25(4) = $5.00
If x = 5 then y = 1.25(5) = $6.25
B. Can the relationship between the weight and the number of avocados be described with a constant rate? Explain.
______________________
______________________
______________________
Check Understanding
Question 1.
A 2-pound package of hamburger costs $7.00, and you pay $10.50 for a 3-pound package of hamburger. Complete the table. Then decide whether it makes sense to use a constant rate to describe the relationship. Explain.

_________________
Answer:
Given,
A 2-pound package of hamburger costs $7.00, and you pay $10.50 for a 3-pound package of hamburger.

Weight/cost = (3-2)/(10.5 – 7) = 0.28
Weight/cost = (4-3)/(14 – 10.5) = 0.28
Thus it makes sense to use a constant rate to describe the relationship.
Question 2.
The table shows the total costs of different numbers of tickets. Decide whether it makes sense to use a constant rate to describe the relationship. Explain.

Answer:
Number of tickets/total cost = (8 – 6)/(44 – 34.5) = 0.21
Number of tickets/total cost = (10 – 8)/(52.5 – 44) = 0.23
0.21 ≠ 0.23
Thus it does not make sense to use a constant rate to describe the relationship.
On Your Own
Question 3.
Reason Flo measures the amount of water her high pressure sprayer uses and finds that it uses 20 gallons of water in 4 minutes and 30 gallons in 6 minutes. Complete the table. Then decide whether it makes sense to use a constant rate to describe the relationship. Explain.

Answer:

(4 – 2)/(20 – 10) = 2/10 = 0.2
(6 – 4)(30 – 20) = 2/10 = 0.2
Thus the relationship between time and water can be described by a constant rate.
For Problems 4-5, use the given information.
Ken rode his bike on Monday and Tuesday. Each table shows the distance that he was from home at various times.
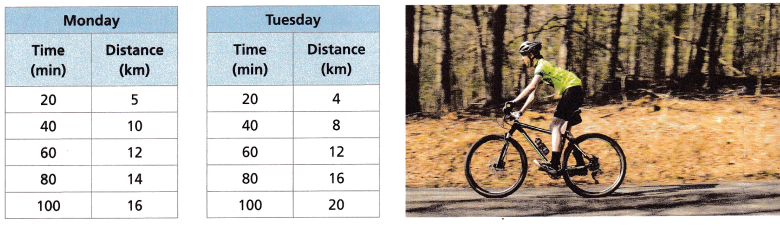
Question 4.
Can the relationship in Monday’s table be described by a constant unit rate? Explain.
______________________
Answer:
The rate between 20 and 40 min = (10 – 5)/(40 – 20) = 5/20 = 0.25
The rate between 40 and 60 min = (12 – 10)/(60 – 40) = 2/20 = 0.1
0.25 ≠ 0.10
Therefore the relationship in Monday’s table cannot be described by a constant unit rate.
Question 5.
Can the relationship in Tuesday’s table be described by a constant unit rate? Explain.
______________________
Answer:
The rate between 20 and 40 min = (8 – 4)/(40 – 20) = 4/20 = 0.2
The rate between 40 and 60 min = (12 – 8)/(60 – 40) = 4/20 = 0.2
0.2 = 0.2
Therefore the relationship in Monday’s table can be described by a constant unit rate.
I’m in a Learning Mindset!
What can I apply from previous work with ratios and rates to recognize when a relationship between two quantities can be described by a constant unit rate?
_______________________
_______________________
Lesson 1.1 More Practice/Homework
Explore Relationships
Question 1.
The amount of money Chaz earned for walking dogs is given in the table. Can the relationship be described by a constant rate? Explain.

Answer:
The above table shows the number of steps dogs walked and the money earned.
Constant rate = (150 – 112.5)/(8 – 6)
= 37.5/2 = 18.75
11 × 18.75 = 206.25
Hence the constant rate is 18.75
Question 2.
STEM The diagram shows the structure of a molecule of sulfur dioxide. The ratio of oxygen atoms to sulfur atoms in sulfur dioxide is always the same. How many oxygen atoms (O) are there when there are 6 sulfur atoms (S)? Explain how you got your answer.
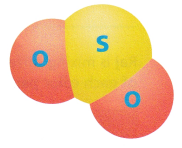
Answer:
Given,
The ratio of oxygen atoms to sulfur atoms in sulfur dioxide is always the same
We know that the ratio of oxygen of atoms to sulfur atoms in the sulfur dioxide is 2:1
So, if 6 sulfur atoms are there then 2 × 6 = 12 oxygen atoms are there.
Question 3.
Reason Three different sizes of sports—drink mix are shown with their prices. Can the relationship between price and volume (in grams) be described by a constant rate? Explain.

Answer:
Three different sizes of sports—drink mix are shown with their prices.
9/150 = 0.06
22.75/325 = 0.07
12.5/250 = 0.05
So, there is no constant rate.
For Problems 4—5, use the values in the table.

Question 4.
Can the relationship between cups of milk and cups of cereal be described by a constant ratio? Why or why not?
Answer:
Cups of cereal/ cups of milk = 12/4 = 3 and 18/6 = 3
So, the constant ratio is 1/3
Question 5.
Can the relationship. between cups of cereal and servings of cereal be described by a constant rate? Why or why not?
Answer:
cups of cereal/ servings of cereal = 12/16 = 3/4 and 18/24 = 3/4 = 0.75
So, the rate is 0.75 or 3/4.
Test Prep
Question 6.
Jane is saving to buy a cell phone. She is given a $100 gift to start and saves $35 a month from her allowance. So after 1 month, Jane has saved $135. Does it make sense to represent the relationship between the amount saved and the number of months with one constant rate? Why or why not? Explain your answer.
Answer:
Given,
Jane is saving to buy a cell phone. She is given a $100 gift to start and saves $35 a month from her allowance.
So after 1 month, Jane has saved $135
Let the number of months be x.
Every month she saved $35
So, the relationship is 35x + 100.
Question 7.
Raj is mixing different colors of paint. The table shows the amount of each color paint Raj uses for each mixture.
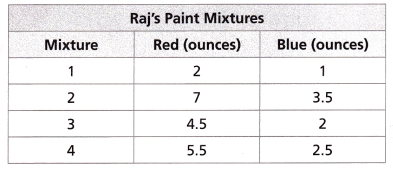
Select the two mixtures that will produce the same color.
A. mixtures 1 and 2
B. mixtures 3 and 4
C. mixtures 1 and 3
D. mixtures 2 and 4
Answer:
Mixture 1: 2:1
Mixture 2: 7 : 3.5 = 2 : 1
Mixture 3: 4.5 : 2
Mixture 4: 5.5 : 2.5
So, Mixture 1 and 2 will produce the same color.
Thus option A is the correct answer.
Spiral Review
Question 8.
At 1:00 p.m., a diver’s elevation is -30 feet relative to sea level. At 2:00 p.m., the diver’s elevation is -45 feet. At which time is the diver farther from sea level?
Answer:
Given,
At 1:00 p.m., a diver’s elevation is -30 feet relative to sea level.
tan 30° = P/B
1/√3 = P/B
P1 = B/√3
At 2:00 p.m., the diver’s elevation is -45 feet.
tan 45° = P/B
1= P2/B
P2 = B
So, at 2:00 pm, diver will be farther away from the sea level.
Question 9.
A share of stock costs $83.60. The next day, the price increases $15.35. The following day, the price decreases $4.75. What is the final price?
Answer:
Given,
A share of stock costs $83.60.
The next day, the price increases $15.35.
83.60 + 15.35 = $98.95
The following day, the price decreases $4.75.
$98.95 – $4.75 = $94.20
Hence the final price is $94.20