We included HMH Into Math Grade 7 Answer Key PDF Module 1 Identify and Represent Proportional Relationships to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Answer Key Identify and Represent Proportional Relationships
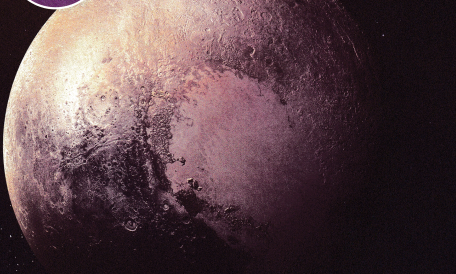
Astronomer
Michael E. Brown is a professor of planetary astronomy at the California Institute of Technology and the author of the book How I Killed Pluto and Why It Had It Coming. Brown and his team discovered a number of objects in our solar system farther away than Neptune. One of these objects, the dwarf planet Eris, is more massive than Pluto (shown above). This discovery resulted in The International Astronomical Union demoting Pluto to a dwarf planet.

STEM Task
We often use ratios to describe scale models. If a model rocket has a scale 1 inch = 12 feet, that means for every part of the model that measures 1 inch the corresponding part of the rocket measures 12 feet. Use this scale to calculate the height of a rocket if the model is 26 inches tall. Explain your reasoning.
Learning Mindset
Perseverance Collects and Tries Multiple Strategies

Perseverance is the ability to stick with a task, even if it is difficult. Have you ever noticed that you are able to manage your time on tasks better than before or that you are able to identify study skills that are effective for you? Those are signs that your ability to persevere is growing. Here are some tips for helping you persevere through difficult tasks.
- Get rid of distractions, like your cell phone, while you are working. Your brain is less effective when you attempt to multi-task. All human brains are! That’s because multi-tasking isn’t really doing two things at once. Your brain is actually shifting attention between the activities, and that slows you down. It can also make the quality of your work decrease.
- Divide complex tasks into smaller steps. This helps you focus your efforts. It also makes it easier to spot mistakes.
- Even if your effort is unsuccessful, look at what you can learn from each attempt and adjust your strategy.
- Check for a fixed-mindset voice in your head telling you that you’re not good with certain content or with certain tasks. Activate your growth-mindset voice telling you that you can learn more about the content and get better at the tasks.
Reflect
Question.
What are some strategies you used to manage your time while working on the STEM Task?
Answer:
Question.
How have you kept yourself on task in the past? What is your plan for improving your ability to stay focused as you face math challenges?
Which Ratio Does Not Belong?
Express each ratio of apples to oranges shown below in words and as a fraction. Share with a partner or a small group.
A.

Answer:
There are 4 apples and 9 oranges in the above figure.
The ratio of apples to oranges is 4:9
The fraction form of the ratio is 4/9

B.

Answer:
Number of apples = 1
Number of oranges = 2
The ratio of apples to oranges is 1:2
The fraction form of the ratio is 1/2

C.
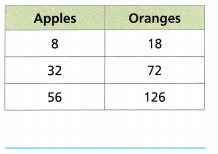
Answer:
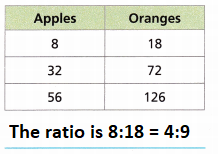
D.

Answer: Ratio of apples to oranges is 4:9
Turn and Talk
- Explain how the ratios are related and how they are different.
- Which ratio does not belong? Explain why.
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Solve One-Step Equations
Solve the equation.
Question 1.
8x = 56 _____
Answer:
Given equation
8x = 56
x = 56/8
x = 7
Question 2.
4a = 23 ____
Answer:
4a = 23
a = 23/4
a = 5.75
Ordered Pairs on the Coordinate Plane
Write the ordered pair for each point.
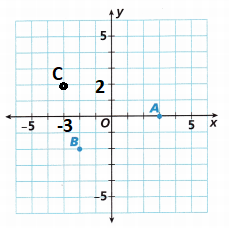
Question 3.
A _____
Answer: The ordered pair A as per the graph is (3,0)
Question 4.
B ____
Answer: The ordered pair B as per the graph is (-2,-2)
Plot and label the ordered pairs on the graph.
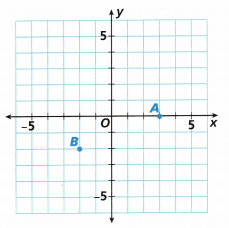
Question 5.

Answer:
-3 on the x-axis and 2 on the y-axis.
Locate the point C on (-3, 2)
Question 6.

Answer:
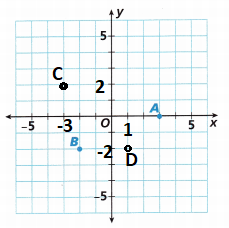
1 on the x-axis and -2 on the y-axis.
Locate the point D on (1, -2)
Divide Fractions and Mixed Numbers
Divide.
Question 7.
\(\frac{3}{4}\) ÷ \(\frac{3}{5}\) _____
Answer:
Given fractions,
\(\frac{3}{4}\) ÷ \(\frac{3}{5}\)
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication.
\(\frac{3}{4}\) × \(\frac{5}{3}\) = \(\frac{5}{4}\)
Convert from improper fraction to the mixed fraction.
\(\frac{5}{4}\) = 1\(\frac{1}{4}\)
Question 8.
7\(\frac{1}{2}\) ÷ \(\frac{5}{8}\) _____
Answer:
Given fractions,
7\(\frac{1}{2}\) ÷ \(\frac{5}{8}\)
7\(\frac{1}{2}\) = \(\frac{15}{2}\)
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication.
\(\frac{15}{2}\) ÷ \(\frac{5}{8}\)
\(\frac{15}{2}\) × \(\frac{8}{5}\) = \(\frac{120}{10}\) = 12
Question 9.
\(\frac{3}{8}\) ÷ \(\frac{1}{2}\) _____
Answer:
Given fractions,
\(\frac{3}{8}\) ÷ \(\frac{1}{2}\)
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication.
\(\frac{3}{8}\) × \(\frac{2}{1}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Ratio Language
Question 10.
Jasper has a jar of marbles. Complete the table to show the ratios of marbles.


Answer:
Number of red marbles = 3
Number of yellow marbles = 2
Number of blue marbles = 6
