We included HMH Into Math Grade 6 Answer Key PDF Module 9 Lesson 2 Use Addition and Subtraction Equations to Solve Problems to make students experts in learning maths.
HMH Into Math Grade 6 Module 9 Lesson 2 Answer Key Use Addition and Subtraction Equations to Solve Problems
I Can write and solve equations using addition and subtraction to represent real-world situations involving an unknown.
Spark Your Learning
Thomas has four jugs of different sizes. One holds 1.2 liters, one holds 1.3 liters, one holds 2.3 liters, and one holds 2.6 liters. He has to fill a large barrel with exactly 5 liters of water. How can he use the jugs to pour this amount into the barrel? Find as many ways as possible.

Answer:
Given that,
Thomas has four jugs of different sizes.
One holds 1.2 liters
One holds 1.3 liters
One holds 2.3 liters
One holds 2.6 liters
He has to fill exactly 5 liters of the barrel.
The number of possible ways to fill the barrel is
Pour two times 1.2 liters and 2 times 1.3 liters.
Pour one time 2.6 liters and two times 1.2 liters.
The number of possible ways is 2.
Turn and Talk Explain how you could measure exactly 0.1 liter, exactly 1 liter, and exactly 1.4 liters by pouring water from one jug to another.
Build Understanding
When solving an addition equation, you can model the equation on a balance scale. For the equation to remain true, both sides must remain equal or, in the case of a balance scale, be the same weight. If you remove something from one side, you must remove the same amount from the other side.
Question 1.
Weights are shown on the scale. Each square is 1 unit, but the value of the triangle x is unknown. The scale sides are balanced.
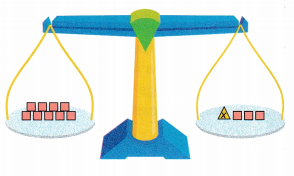
A. Describe the weights on the left side of the scale and on the right side of the scale using both words and mathematical expressions.
Answer:
The number of squares on the left side is 9
1 square = 1 unit.
Therefore 9 x 1 = 9 units.
There are 9 units on the left side.
The number of squares on the right side is 3 and one x is an unknown weight.
So, 3 + x units on the right side.
The mathematical expression is 9 = 3 + x.
In words, nine = three plus x.
B. What equation represents the weights shown on the scale?
Answer: The equation 9 = 3 + x represents the weights shown on the scale.
C. How could you remove weights, making sure that the scale is still balanced, and use that to find the value of x?
Answer:
The equation is 9 = 3 + x
9 – 3 = x
x = 6
Remove 6 units from the left side and x from the right side then the scale is still balanced.
D. As if you were removing weights from both sides of the scale, cross out the same number of weights on both sides of the scale until x is by itself. How much must the weight labeled x weigh? Explain how you know.
Answer:
If you remove the 3 squares from both sides. The scale has the x units weight remaining.
After removing 3 units, the weight of x is 6 on the right side.
After removing 3 units the weight is 6 units on the left side.
Therefore both sides are balanced.
E. Check your answer by substituting the value of x into the equation from Part B. Explain your work.
Answer:
The equation is 9 = x + 3
The x value is 6
Substitute x = 6 in the above equation is 9 = 6 + 3
9 = 9
Turn and Talk If one side of a balance ¡s lower than the other side, what mathematical symbol could you use to describe what the balance shows?
Answer: We use less than a symbol to describe what the balance shows in the equation.
Step It Out
Question 2.
A plant is 6 inches tall. After 2 weeks, the plant is 14 inches tall. How many inches did the plant grow?
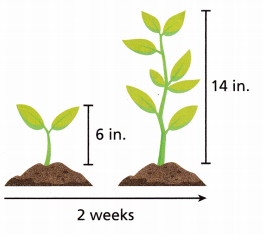
A. What information do you know?
The plant starts at ![]() inches.
inches.
The plant grows to ![]() inches.
inches.
Answer:
The plant starts at 6 inches.
The plant grows to 14 inches.
B. What do you need to find out?
Answer: We need to find out How many inches did the plant grow?
C. You can represent how many inches the plant grew in two weeks with a variable x. How can you describe the relationship between the unknown amount x and the height of the plant at the start?
Answer:
x + 6 = 14
D. Write an equation you can solve in order to answer the problem.
![]() +
+ ![]() =
= ![]()
Answer:
x + 6 = 14
E. You can also model the problem using algebra tiles. The sets of tiles on both sides of the gray rule are equal. Just like with a scale, if you remove one tile from one side, you must also remove one tile from the other side. Cross out tiles until x is by itself. How many tiles did you cross out on each side? How many tiles remain on the right side of the model?

![]() 1-tiles were crossed out on each side.
1-tiles were crossed out on each side.
![]() 1-tiles are left on the right side.
1-tiles are left on the right side.
Answer:
6 1-tiles were crossed out on each side.
14 1-tiles are left on the right side.
x + 6 = 14
x = 14 – 6
x = 8
F. What is the solution to the equation?
Answer: 8 is the solution to the equation.
G. Check your answer by substituting the value for x into the equation from Part D and combine like terms then solve. Is your answer correct?
Answer:
x + 6 = 14
8 + 6 = 14
14 = 14
Turn and Talk Which model do you prefer, the scale or algebra tiles? Explain.
Instead of using a scale or algebra tiles, you can subtract the same amount from both sides of an equation and the two sides will remain equal. This is known as the Subtraction Property of Equality.
Question 3.
Sara had $8.50 in her pocket. She earned m dollars babysitting and now she has $20.25. How much did she earn babysitting?

A. What does m represent?
Answer:
Given that,
Sara had $8.50 in her pocket
She earned m dollars babysitting
Now she has $20.25
The m represents the number of dollars she earned by babysitting.
m = $20.25 – $8.50 = $11.75
B. Write an equation for this situation.
$ ![]() +
+ ![]() = $
= $![]()
Answer:
Sara had $8.50 in her pocket
m = $11.75
The equation is $8.50 + $11.75 = $20.25.
C. How much do you need to subtract from both sides of the equation to get an equation with only m on the left side?
Answer:
8.50 + m = 20.25
D. Subtract ![]() from both sides to isolate m. 8.50 + m = 20.25
from both sides to isolate m. 8.50 + m = 20.25
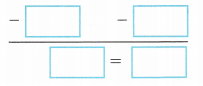
Answer:
8.50 + m = 20.25
Subtract 8.50 on both sides.
8.50 + m – 8.50 = 20.25 – 8.50
m = 11.75
E. Sara earned $ ![]() babysitting.
babysitting.
Answer: Sara earned $11.75 for babysitting.
Question 4.
You can also add the same amount to both sides of an equation and the two sides will remain equal. This is the Addition Property of Equality.
A. Solve the equation x – 7 = 12 by adding ![]() to each side.
to each side.
Answer:
Given equation x – 7 = 12
By adding 7 to each side we can solve the equation.
B. x – 7 = 12
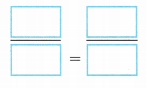
Answer:
x – 7 = 12
x – 7 + 7 = 12 + 7
x = 19
Check Understanding
Question 1.
Jerry has two dogs. The older one weighs 95 pounds. Their combined weight is 120 pounds. Write and solve an equation to find the younger dog’s weight d. What number did you subtract from both sides?
Answer:
Given,
Jerry has two dogs. The older one weighs 95 pounds.
Their combined weight is 120 pounds.
The equation would be
95 + d = 120
d = 120 – 95
d = 25
For Problems 2-4, add or subtract to solve the equation, circle the correct word, and state the number that you added or subtracted.
Question 2.
x – 15 = 29, x = ![]()
Answer:
x – 15 = 29
Add 15 on both sides
x – 15 + 15 = 29 + 15
x = 44
Question 3.
12.26 + w = 39, w = ![]()
Answer:
12.26 + w = 39
Subtract 12.26 on both sides to solve w.
12.26 + w – 12.26 = 39 – 12.26
w = 26.74
Question 4.
y – \(\frac{3}{4}\) = 4\(\frac{1}{4}\), y = ![]()
Answer:
y – \(\frac{3}{4}\) = 4\(\frac{1}{4}\)
Add \(\frac{3}{4}\) on both sides.
y – \(\frac{3}{4}\) + \(\frac{3}{4}\) = 4\(\frac{1}{4}\) + \(\frac{3}{4}\)
y = 5
On Your Own
Question 5.
Model with Mathematics Annie is the height shown. She is 49 centimeters taller than her brother. Write and solve an equation to find her brother’s height b in centimeters.

Answer:
Given,
Annie is 152.5 cm tall.
She is 49 centimeters taller than her brother.
b + 49 = 152.5
b = 152.5 – 49
b = 103.5 cm
Question 6.
Critique Reasoning For the equation z – 14 = 29, Juan says that the solution is 33. Check whether Juan’s solution works by substituting it into the equation and combining like terms. Is his solution correct?
Answer:
z – 14 = 29
z = 29 + 14
z = 43
Juan’s solution is not correct.
Question 7.
William buys a book for $14.85. If he pays with a $20 bill, what will change c be? Write and solve an equation to find out.
Answer:
Given,
William buys a book for $14.85.
He pays with a $20 bill
14.85 + c = 20
c = 20 – 14.85
c = 5.15
Question 8.
Van had 5 trading cards, and then his friend gave him more cards. Now he has 16 trading cards. Let t represent the number of cards his friend gave him. Write both an addition equation and a subtraction equation to model the problem.
![]() + t =
+ t = ![]()
![]() –
– ![]() = t
= t
Answer:
Van had 5 trading cards, and then his friend gave him more cards.
Now he has 16 trading cards. Let t represent the number of cards his friend gave him.
5 + t = 16
t = 16 – 5
t = 11
Question 9.
The scale shows the equation 7 = r + 5. Cross out the same number of tiles on each side to get r by itself. What is the value of r?
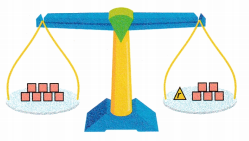
r = ____________
Answer:
Given,
The scale shows the equation 7 = r + 5.
Cross out the same number of tiles on each side to get r by itself.
7 = r + 5
7 – 5 = r
r = 2
The value of r is 2.
For Problems 10-15, circle whether you add or subtract to solve the equation. Then find the value.
Question 10.
8 + x = 42, (add / subtract), x = ![]()
Answer:
8 + x = 42
Subtract 8 on both sides
8 + x – 8 = 42 – 8
x = 34
Question 11.
w – 61 = 14, (add / subtract), w = ![]()
Answer:
w – 61 = 14
Add 61 on both sides
w – 61 + 61 = 14 + 61
w = 75
Question 12.
n – 81 = 67, (add / subtract), n = ![]()
Answer:n – 81 = 67
To find the value of n we have to add 81 on both sides
n – 81 = 67
n – 81 + 81 = 67 + 81
n = 148
Question 13.
m + 3.89 = 9.02, (add / subtract), m = ![]()
Answer:
m + 3.89 = 9.02
To find the value of m we have to subtract 3.89 on both sides
m + 3.89 – 3.89 = 9.02 – 3.89
m = 5.13
Question 14.
y + 2.4 = 6.75, (add / subtract), y = ![]()
Answer:
y + 2.4 = 6.75
To find the value of y we have to subtract 2.4 on both sides
y + 2.4 – 2.4 = 6.75 – 2.4
y = 4.35
Question 15.
c + \(\frac{5}{9}\) = \(\frac{8}{9}\), (add / subtract), c = ![]()
Answer:
c + \(\frac{5}{9}\) = \(\frac{8}{9}\)
To find the value of c we have to subtract \(\frac{5}{9}\) on both sides
c + \(\frac{5}{9}\) – \(\frac{5}{9}\) = \(\frac{8}{9}\) – \(\frac{5}{9}\)
c = \(\frac{3}{9}\)
c = \(\frac{1}{3}\)
Question 16.
Model with Mathematics Jasmine is training for a race. Her goal is to cover 28 miles this week. So far this week, she has gone the distances shown. Write and solve an equation to find the number of miles m Jasmine has left to meet her goal.

Answer:
Given,
Jasmine is training for a race. Her goal is to cover 28 miles this week.
Monday = 6 miles
Tuesday = 8 miles
Wednesday = 6 miles
6 + 8 + 6 = 20 miles
The equation to find the number of miles m Jasmine has left to meet her goal would be
20 + x = 28
x = 28 – 20
x = 8
Thus 8 miles are left to reach her goal.
Question 17.
Aviva has collected 56 cans of food for disaster relief. Her goal is to collect 200 cans. Write and solve an equation to show how many more cans c she needs to reach her goal.
Answer:
Given,
Aviva has collected 56 cans of food for disaster relief.
Her goal is to collect 200 cans.
Let c be the number of cans to reach her goal.
56 + c = 200
c = 200 – 56
c = 144
Thus 144 cans she needs to reach her goal.
Question 18.
The Gateway Arch in St. Louis, Missouri, is 630 feet tall. It is 75 feet taller than the Washington Monument in Washington, D.C. Write and solve an equation to find the height h of the Washington Monument.
Answer:
Given,
The Gateway Arch in St. Louis, Missouri, is 630 feet tall.
It is 75 feet taller than the Washington Monument in Washington, D.C.
The equation would be
h + 75 = 630
h = 630 – 75
h = 555
Thus the height of the Washington Monument is 555 feet.
Question 19.
Show that 1.27 is not a solution for the equation g + 3.74 = 5.1. Then find the correct solution and show why it is correct.
Answer:
Given equation,
g + 3.74 = 5.1
g = 5.1 – 3.74
g = 1.36
Hence it is proven that 1.27 is not a solution.
Question 20.
The balance shows the equation b + 6 = 10. What is the value of b?
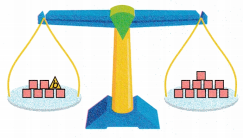
b = ___________
Answer:
The balance shows the equation b + 6 = 10
b + 6 = 10
b = 10 – 6
b = 4
For Problems 21-22, add or subtract to solve the equation.
Question 21.
8.7 + x = 12.05, x = ____________
Answer:
8.7 + x = 12.05
Subtract 8.7 on both sides
x + 8.7 – 8.7 = 12.05 – 8.7
x = 3.35
Question 22.
a – 34 = 60, a = ____________
Answer:
a – 34 = 60
Adding 34 on both sides
a – 34 + 34 = 60 + 34
a = 94
I’m in a Learning Mindset!
How do I know when solving addition and subtraction equations triggered a fixed-mindset response in a classmate?
Answer:
First, we have to identify the operation being performed on the variable. Apply the inverse operation on both sides. And then solve the unknown value.
Lesson 9.2 More Practice/Homework
Math on the Spot For Problems 1-3, solve each equation. Check your answer.
Question 1.
s – 5 = 12 ___________
Answer:
s – 5 = 12
s = 12 + 5
s = 17
Question 2.
35 = y – 6 ____________
Answer:
35 = y – 6
y – 6 = 35
Add 6 on both sides
y – 6 + 6 = 35 + 6
y = 41
Question 3.
x – 22 = 44 ___________
Answer:
x – 22 = 44
Add 22 on both sides
x – 22 + 22 = 44 + 22
x = 66
Question 4.
Model with Mathematics Mary compares the heights of two trees. Their heights are shown. Write and solve an equation to find the height h of the taller tree.
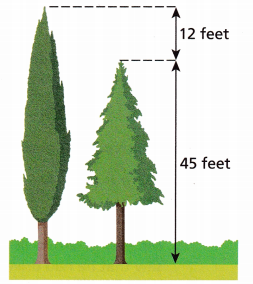
Answer:
Given,
Mary compares the heights of two trees.
Their heights are shown in the above figure.
45 + 12 = h
h = 57 feet
Thus the height of the taller tree is 57 feet.
Question 5.
Open-Ended Write an equation with a solution of 25. Use the variable x and addition.
Answer:
x = 25
6x = 25 + 5x
Multiply 0.25 on both sides
1.5x = 6.25 + 1.25x
Now subtract 1.25x on both sides
1.5x – 1.25x = 6.25 + 1.25x – 1.25x
0.25x = 6.25
x = 6.25/0.25
x = 25
Question 6.
Each small square on this scale weighs 1 unit. Each larger square weighs 10 units. The weight of the triangle x is unknown. The scale is balanced. What is the weight of the triangle?

A. Model with Mathematics Write an equation to represent the weights shown on the scale.
Answer:
Given,
Each small square on this scale weighs 1 unit.
Each larger square weighs 10 units.
The weight of the triangle x is unknown.
The equation would be x + 22 = 34
B. Cross out the same weights on each side until x is alone. What is the total weight that you crossed out on each side?
Answer:
The weights are given as
small square = 1
larger square = 10
The total weight on one side, where there are 4 small squares and 3 large squares is
Total = 4 × small square + 3 × larger square
Total = 4 × 1 + 3 × 10
Total = 4 + 30 = 34
C. Write the simplified equation represented by the scale now. What is the weight of the triangle?
Answer:
The total weight on the other side, where there are 2 small squares, 2 large squares and 1 triangle
Total = 2 × small square + 2 × larger square + 1 × triangle
Total = 2 × 1 + 2 × 10 + 1 × triangle
Total = 2 + 20 + 1 triangle
Total = 22 + x
Thhus the weight of the triangle is 22 + x.
For Problems 7-8, determine whether the given value is a solution for the equation. Write is or is not on the line.
Question 7.
x – 14 = 42, x = 56
56 __________ a solution.
Answer:
x – 14 = 42
x = 56
56 – 14 = 42
42 = 42
So, 56 is a solution.
Question 8.
k + 66 = 98, k = 28
28 ___________ a solution.
Answer:
k + 66 = 98
k = 28
28 + 66 = 98
94 ≠ 98
Thus 28 is not a solution.
For Problems 9-10, solve the equation.
Question 9.
55 + s = 110, s = ____________
Answer:
55 + s = 110
s = 110 – 55
s = 55
Question 10.
n – 52 = 12, n = _____________
Answer:
n – 52 = 12
Add 52 on both sides
n – 52 + 52 = 12 + 52
n = 64
Question 11.
What value for w makes the equation 76 + w = 100 true?
Answer:
76 + w = 100
w = 100 – 76
w = 24
Question 12.
Which equations have x = 15 as a solution? Select all that apply.
(A) x + 14 = 29
(B) 25 + x = 10
(C) x – 38 = 23
(D) x + 17 = 32
(E) x – 8 = 7
(F) 35 – x = 25
Answer:
(A) x + 14 = 29
(D) x + 17 = 32
(E) x – 8 = 7
Explanation:
(A) x + 14 = 29
x = 29 – 14
x = 15
(B) 25 + x = 10
x = 10 – 25
x = -15
(C) x – 38 = 23
x = 23 + 38
x = 70
(D) x + 17 = 32
x = 32 – 17
x = 15
(E) x – 8 = 7
x = 7 + 8
x = 15
(F) 35 – x = 25
35 – 25 = x
x = 10
Thus Option A, D and E are the correct answers.
Question 13.
What must you do to both sides to solve the equation g – 24 = 36? Circle the correct response and fill in the blank.
(Add / Subtract) __________ (to / from) both sides.
Answer:
g – 24 = 36
Add 24 to both sides
g – 24 + 24 = 36 + 24
g = 60
Question 14.
Which value is a solution to the equation \(\frac{7}{12}\) + n = \(\frac{5}{6}\)?
(A) n = \(\frac{10}{7}\)
(B) n = \(\frac{1}{4}\)
(C) n = \(\frac{1}{3}\)
(D) n = \(\frac{17}{12}\)
Answer:
\(\frac{7}{12}\) + n = \(\frac{5}{6}\)
n = \(\frac{5}{6}\) – \(\frac{7}{12}\)
n = \(\frac{10}{12}\) – \(\frac{7}{12}\)
n = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Option B is the correct answer.
Question 15.
Mr. Renner drove 18 miles to work. He drove home a different way and saw that he had driven a total of 41 miles that day. How many miles was the drive home?
Answer:
Given,
Mr. Renner drove 18 miles to work.
He drove home a different way and saw that he had driven a total of 41 miles that day.
41 – 18 = 23 miles
Spiral Review
Question 16.
What is the value of \(\frac{4}{5}\) × \(\frac{3}{4}\) in simplest form?
Answer:
\(\frac{4}{5}\) × \(\frac{3}{4}\)
Cancel 4 and 4 from the numerator and denominator.
\(\frac{4}{5}\) × \(\frac{3}{4}\) = \(\frac{3}{5}\)
Question 17.
Which is a lower price per pound, 4 pounds for $1.40 or 3 pounds for $1.20? Show each as a unit rate.
Answer:
4 pounds for $1.40
1 pound = x
x × 4 = 1.40
x = 1.40/4
x = 0.35
One pound is $0.35
3 pounds for $1.20
1 pound = y
y × 3 = 1.20
y = 1.20/3
y = 0.40
Evaluate the expression.
Question 18.
23 ____________
Answer:
23 = 2 × 2 × 2 = 8
Question 19.
34 ____________
Answer:
34 = 3 × 3 × 3 × 3 = 81
Question 20.
110 ____________
Answer:
110 = 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Question 21.
103 ____________
Answer:
103 = 10 × 10 × 10 = 1000