We included HMH Into Math Grade 6 Answer Key PDF Module 9 Lesson 1 Write Equations to Represent Situations to make students experts in learning maths.
HMH Into Math Grade 6 Module 9 Lesson 1 Answer Key Write Equations to Represent Situations
I Can write and solve equations that model real-world situations involving all four operations.
Spark Your Learning
Bella and Tia began the week with the same amount of money. Bella paid $9 to go to the movies. Tia spent $2 on snacks and $7 on a new T-shirt. Do Bella and Tia have the same amount of money left? Explain how you know.

Answer:
Given,
Bella and Tia began the week with the same amount of money. Bella paid $9 to go to the movies. Tia spent $2 on snacks and $7 on a new T-shirt.
7 + 2 = 9
Both spend the same amount of money.
Turn and Talk How would your representation of the problem change if both people earned money instead of spending money?
Answer:
Build Understanding
Connect to Vocabulary
An equation is a mathematical sentence that shows that two expressions are equivalent.
Question 1.
YOU can think of an equation as a balance scale that is level with equal weight on both sides. The scale shows two quantities that have equal weight.
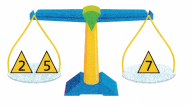
A. What does the left side of the scale show? Write your answer in words. Then write a mathematical expression using addition that represents the weight on the left side.
Answer:
The left side of the scale shows the weights 2 and 5
The answer in the words is the addition of two and five.
The mathematical expression that represents the weight on the left side is 2 + 5 = 7.
B. What does the right side of the scale show? Write your answer in words. Then write an integer that represents the weight on the right side.
Answer:
The weight shown on the right side of the scale is 7.
The answer in the words is seven.
The integer is 7 which represents the weight on the right side.
C. What equation does the scale represent?
Answer: The scale representing the equation is 2 + 5 = 7.
D. If the 2-unit weight is removed, will the scale remain balanced? What would the scale show if the 2-unit weight were removed?
Answer:
The 2 unit weight is removed from the scale. The scale is not balanced.
After removing 2 unit weights the scale shows 5 units on the left side and 7 units on the right side.
Question 2.
If a scale is balanced but a value is unknown, you can solve for the unknown value.

A. What equation does the scale represent?
Answer:
The scale represents the equation is 4 + 5 = 6 + x
B. How can you solve for x?
Answer:
9 = 6 + x
9 – 6 = x
x = 3
C. Would other values of x keep the scale balanced? Explain.
Answer:
The value of x = 3 keeps the scale balanced.
Except 3 no other values can balance the scale.
Turn and Talk Do you think an equation with one variable can have more than one solution? Explain.
Answer:
Step It Out
Question 3.
Ben buys tickets for the outdoor skating rink as shown. Each ticket costs the same amount. How much does 1 ticket cost?

A. What information do you know?
Ben bought ![]() tickets. Ben spent $
tickets. Ben spent $ ![]() .
.
Answer: We know that Ben bought 4 tickets. Ben spent $72
B. What do you need to find out?
Answer: We need to find out how much does 1 ticket cost.
C. You can represent the cost of a ticket with the variable c. How are the unknown amount c and the amount Ben spent related?
Answer: The equation to represent the cost of a ticket with the variable c is 4c = 72
D. Model the situation using an equation, thinking about the different parts. Write the value or variable for each part of the model.

Answer: 4 × c = 72
c = 72/4
c = 18
Thus the cost of each ticket is $18.
Connect to Vocabulary
A solution of an equation is a value that makes the equation true.
E. Substitute values for c to find the solution. Try c = 20.
When c = 20, the left side of the equation is ____________ 72,
so c = 20 (is / is not) a solution of the equation.
Answer:
4 × c = 72
If c = 20
4 × 20 = 72
80 ≠ 72
So, c = 20 is not a solution.
F. Try other values for c, thinking about how close your result is to 72. What ¡s the solution for the equation? How much does a ticket cost?
When c = ![]() , 4 × c = 72. Each ticket costs
, 4 × c = 72. Each ticket costs ![]() .
.
Answer:
c = 72/4
c = 18
Thus the cost of each ticket is $18.
Check Understanding
Question 1.
There are 30 students in a class. Today, 26 students are present. Write and solve an equation to show how many students are absent.
Answer:
Given,
There are 30 students in a class.
Today, 26 students are present.
26 + a = 30
a = 30 – 26
a = 4
Thus 4 students are absent.
For Problems 2-4, determine whether the given value is a solution for the equation. Answer yes or no.
Question 2.
x – 8 = 12, x = 4
Answer:
x – 8 = 12
x = 4
4 – 8 = 12
-4 ≠ 12
The value is not the solution for the equation.
Question 3.
12w = 36, w = 3
Answer:
12w = 36
w = 3
12 × 3 = 36
36 = 36
The value is the solution for the equation.
Question 4.
\(\frac{y}{8}\) =40, y = 5
Answer:
\(\frac{y}{8}\) =40
y = 5
y = 40 × 8
y = 320
The value is not the solution for the equation.
On Your Own
Question 5.
Model with Mathematics The number of red marbles in a jar is 3 times the number of blue marbles. There are 27 red marbles and b blue marbles. Write an equation to represent this situation. How many blue marbles are there?

Answer:
Given,
The number of red marbles in a jar is 3 times the number of blue marbles.
There are 27 red marbles and b blue marbles.
The equation would be 3b = 27
b = 27/3
b = 9
Thus there are 9 blue marbles.
Question 6.
Model with Mathematics Martha’s daughter is \(\frac{1}{4}\) Martha’s age. If Martha’s daughter is 12 years old, how old is Martha? Write an equation to represent this problem and explain your reasoning. Then find Martha’s age.
Answer:
Given,
Martha’s daughter is \(\frac{1}{4}\) Martha’s age.
x ÷ 12 = \(\frac{1}{4}\)
x = \(\frac{1}{4}\) × 12
x = 3
Thus She is 3 years old.
Question 7.
Shan exercises daily. Today he did 85 pushups, which is 20 more than he usually does. How many pushups p does Shan usually do? Write an equation to represent this situation, and then solve the problem.
Answer:
Given,
Shan exercises daily. Today he did 85 pushups, which is 20 more than he usually does.
p = 85 – 20
p = 65
Question 8.
Critique Reasoning Phillip writes the following equation to show how many hours h he needs to work to earn $108 at $12 per hour: \(\frac{h}{12}\) = 108. Is his equation correct? Explain.
Answer: He is correct because h indicates how many hours he need to work times $12 will give you $108 which means the total cost.
Question 9.
Attend to Precision How are expressions different from equations?
Answer: An expression is a mathematical phrase that contains numbers, variables, or both. Expressions never have an equal sign.
For Problems 10-15, determine whether x = 3, x = 4. or x = 5 is the solution.
Question 10.
8x = 32, x = ![]()
Answer:
8x = 32
x = 32/8
x = 4
Thus x = 4 is the solution.
Question 11.
42 – x = 37, x = ![]()
Answer:
42 – x = 37
42 – 37 = x
x = 5
Thus x = 5 is the solution.
Question 12.
\(\frac{20}{x}\) = 4, x = ![]()
Answer:
\(\frac{20}{x}\) = 4
\(\frac{20}{4}\) = x
x = 5
Thus x = 5 is the solution.
Question 13.
0.5x = 2, x = ![]()
Answer:
0.5x = 2
x = 2/0.5
x = 4
Thus x = 4 is the solution.
Question 14.
\(\frac{x}{3}\) = 1, x = ![]()
Answer:
\(\frac{x}{3}\) = 1
x = 1 × 3
x = 3
Thus x = 3 is the solution.
Question 15.
x + 13 = 16, x = ![]()
Answer:
x + 13 = 16
x = 16 – 13
x = 3
Thus x = 3 is the solution.
I’m in a Learning Mindset!
How do I keep myself motivated to write equations for real-world situations?
Lesson 9.1 More Practice/Homework
Question 1.
Math on the Spot At Glencliff High School, the photography club has 23 members., which is 12 fewer than the hacky sack club. Does the hacky sack club have 35 members or 11 members? Write an equation to model the problem.
Answer:
Given,
At Glencliff High School, the photography club has 23 members., which is 12 fewer than the hacky sack club.
The hacky sack club have 35 members
23 + 12 = 35
35 – 12 = 23
Question 2.
Model with Mathematics Tilda buys a shirt for d dollars. She uses a $50 gift card and receives the change shown. Write an equation for this situation.

Answer:
Given,
Tilda buys a shirt for d dollars. She uses a $50 gift card and receives the change shown.
Change received is $22.50
d = 50 – 22.50
Thus the equation for this solution is d = 50 – 22.50
Question 3.
Open-Ended Write an equation that has a solution of 4. Use the variable n and multiplication.
Answer:
2n = 8
n = 4
2 × 4 = 8
Question 4.
Model with Mathematics One pound is equal to 0.454 kilogram. If Jim has a mass of 50 kilograms, write an equation to represent how many pounds p he weighs.
Answer:
Given,
One pound is equal to 0.454 kilograms.
p pounds is equal to 50 kilograms.
So, the equation would be
0.454p = 50
p = 50/0.454
p = 110.13
Thus Jim weighs 110.13 pounds.
Question 5.
Open-Ended Write a word problem that could be modeled by the equation x + 5 = 12.
Answer: The sum of unknown numbers x and 5 is equal to 12.
Question 6.
Model with Mathematics Jon bought a pizza as shown. Write an equation to find the cost per slice c.

Answer:
The cost of a large pizza is $20.
There are 8 slices in the pizza.
Let the cost per each slice be c.
So, the equation would be
c = 20 ÷ 8
or
8c = 20
c = 2.5
Thus the cost per slice of the pizza is $2.5
For Problems 7-12. write whether the given value is or is not a solution for the equation.
Question 7.
9x = 45, x = 5
5 __________ a solution.
Answer:
9x = 45, x = 5
Substitute the value of x to know whether it is a solution or not.
9(5) = 45
45 = 45
So, the given value is a solution.
Question 8.
k – 6 = 8, k = 2
2 ___________ a solution.
Answer:
k – 6 = 8, k = 2
Substitute the value of k to know whether it is a solution or not.
2 – 6 = 8
-4 ≠ 8
The given value is not a solution.
Question 9.
n + 12 = 20, n = 32
32 __________ a solution.
Answer:
n + 12 = 20, n = 32
Substitute the value of n to know whether it is solution or not.
32 + 12 = 20
44 ≠ 20
The given value is not a solution.
Question 10.
\(\frac{r}{5}\) = 25, r = 125
125 ____________ a solution.
Answer:
\(\frac{r}{5}\) = 25, r = 125
Substitute the value of r to know whether it is solution or not.
\(\frac{125}{5}\) = 25
25 = 25
So, the given value is a solution.
Question 11.
\(\frac{16}{a}\) = \(\frac{1}{2}\), a = 8
8 ___________ a solution.
Answer:
\(\frac{16}{a}\) = \(\frac{1}{2}\), a = 8
Substitute the value of a to know whether it is solution or not.
\(\frac{16}{8}\) = \(\frac{1}{2}\)
2 ≠ \(\frac{1}{2}\)
The given value is not a solution.
Question 12.
24x = 6, x = \(\frac{1}{4}\)
\(\frac{1}{4}\) ____________ a solution.
Answer:
24x = 6, x = \(\frac{1}{4}\)
Substitute the value of x to know whether it is solution or not.
24\(\frac{1}{4}\) = 6
6 = 6
So, the given value is a solution.
Test Prep
Question 13.
Jennifer reads p pages every day. After 15 days, she has read 300 pages. Write an equation to represent this situation.
Answer: p = 20
Explanation:
Given that,
Jennifer reads p pages every day.
After 15 days, she has read 300 pages.
15 × p = 300
p = 300/15
p = 20
Thus she read 20 pages per day.
Question 14.
Jermaine has t trading cards. Jasmine has 7 trading cards. Together, Jermaine and Jasmine have 13 trading cards. Which equation could represent the problem? Select all that apply.
(A) t + 7 = 13
(B) 7 + t= 7
(C) 7t = 13
(D) 7 + t = 13
(E) 13 ÷ t = 7
(F) 13 – 7 = t
Answer:
(A) t + 7 = 13
(D) 7 + t = 13
(F) 13 – 7 = t
Explanation:
Given that,
Jermaine has t trading cards. Jasmine has 7 trading cards.
Together, Jermaine and Jasmine have 13 trading cards.
7 + t = 13
t = 13 – 7
t = 6
Option A, D and F are the suitable answers.
Question 15.
Lily is 5 inches shorter than Dan. If Dan is 67 inches tall, how tall is Lily? Write an equation to model the problem using h for Lily’s height.
Answer:
Given,
Lily is 5 inches shorter than Dan.
Dan is 67 inches tall.
We need to write an equation to model the problem using h for Lily’s height.
Lily’s height plus 5 is equal to Dan’s height.
h + 5 = 67
h = 67 – 5
h = 62
Question 16.
Which value is a solution for the equation \(\frac{m}{4}\) = 16?
(A) m = 4
(B) m = 12
(C) m = 20
(D) m = 64
Answer:
\(\frac{m}{4}\) = 16
m = 16 × 4
m = 64
So, Option D is the correct answer.
Question 17.
Derrick has 72 inches of ribbon to make bows. He uses all of his ribbon to make 9 bows of equal length l. How many inches of ribbon does each bow use? Write an equation to model the situation. Then solve the problem.
Answer:
Given,
Derrick has 72 inches of ribbon to make bows.
He uses all of his ribbons to make 9 bows of equal length l.
Divide ribbons into 9 equal parts.
72 ÷ 9 = 8
8 inches of ribbon is used to make every bow.
Spiral Review
Question 18.
Walter’s sink can hold 12 gallons of water. If it is 85% full, how many gallons of water are in the sink?
Answer:
Given,
Walter’s sink can hold 12 gallons of water.
We need to know how many gallons of water are in the sink if it is 85% full.
85% = 0.85
0.85 × 12 = 10.2
Thus 10.2 gallons of water are in the sink.
Question 19.
A rectangular stage is 6.25 feet long and 12 feet wide. What is the area of the stage in square feet?
Answer:
Given,
A rectangular stage is 6.25 feet long and 12 feet wide.
We know that,
Area of a rectangle = l × w
A = 6.25 × 12
A = 78 sq. feet
Thus the area of the stage is 78 square feet.
Question 20.
Turkey hot dogs come in packages of 6 and buns come in packages of 8. What is the least number of packages that can be bought of each so that there are the same number of hot dogs and buns?
Answer:
Turkey hot dogs come in packages of 6 and buns come in packages of 8.
8 × 6 = 48
Thus the least number of packages that can be bought of each so that there is the same number of hot dogs and buns = 48.
For Problems 21-23, find each quotient.
Question 21.
5\(\frac{1}{4}\) ÷ \(\frac{1}{4}\)
Answer:
5\(\frac{1}{4}\) ÷ \(\frac{1}{4}\)
Convert from mixed fraction to the improper fraction.
5\(\frac{1}{4}\) can be written as \(\frac{21}{4}\)
\(\frac{21}{4}\) ÷ \(\frac{1}{4}\) = \(\frac{21}{4}\) × 4 = 21
Question 22.
1\(\frac{1}{3}\) ÷ \(\frac{2}{3}\)
Answer:
1\(\frac{1}{3}\) ÷ \(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction.
1\(\frac{1}{3}\) can be written as \(\frac{4}{3}\)
\(\frac{4}{3}\) ÷ \(\frac{2}{3}\) = \(\frac{4}{3}\) × \(\frac{3}{2}\) = 2
So, 1\(\frac{1}{3}\) ÷ \(\frac{2}{3}\) = 2
Question 23.
9\(\frac{3}{4}\) ÷ 3\(\frac{1}{4}\)
Answer:
9\(\frac{3}{4}\) ÷ 3\(\frac{1}{4}\)
Convert from mixed fraction to the improper fraction.
9\(\frac{3}{4}\) can be written as \(\frac{39}{4}\)
3\(\frac{1}{4}\) can be written as \(\frac{13}{4}\)
\(\frac{39}{4}\) ÷ \(\frac{13}{4}\)
\(\frac{39}{4}\) × \(\frac{4}{13}\) = 3