Into Math Grade 6 Module 8 Lesson 5 Answer Key Identify and Generate Equivalent Algebraic Expressions

We included HMH Into Math Grade 6 Answer Key PDF Module 8 Lesson 5 Identify and Generate Equivalent Algebraic Expressions to make students experts in learning maths.

HMH Into Math Grade 6 Module 8 Lesson 5 Answer Key Identify and Generate Equivalent Algebraic Expressions

I Can use the properties of operations to determine if two expressions are equivalent and to generate equivalent algebraic expressions.

Step It Out

Question 1.
Kite Substitute the given value into both expressions, and determine if the expressions have the same value.
A. Evaluate when x = 6.

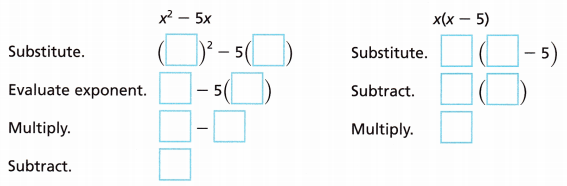
The expressions (do / do not) have the same value when x = 6.
Answer:

B. For the hexagon shown, Linda says the perimeter can be found using the expression 4(\(\frac{s}{2}\)) + 2s. David says that he can use the expression 4s to find the perimeter. Do the expressions have the same value when s = 8?

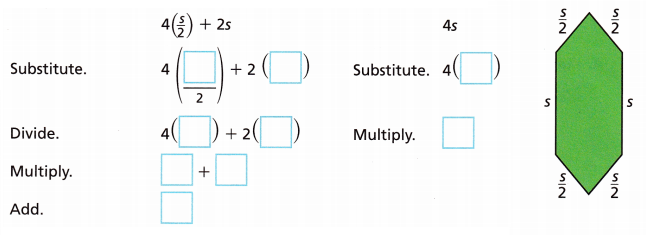
The expressions (do / do not) have the same value when s = 8.
Answer:

Turn and Talk How could you compare the expressions in Part A using the Distributive Property?
Answer:

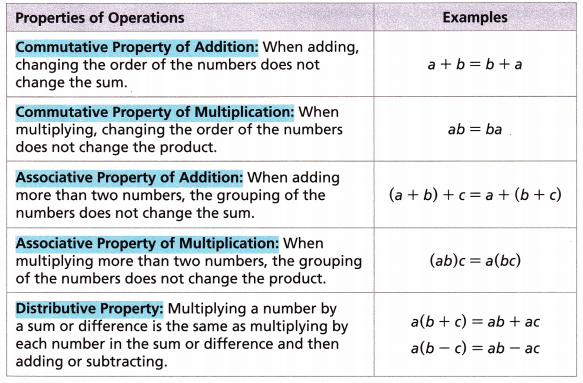
Equivalent expressions are expressions that have the same value for all possible values of the variable. Of course, you can’t check every possible value! Fortunately, there is an easier way to show that expressions are equivalent. You can use the properties of operations. If you can apply the properties to one expression to get the other, then the two expressions are equivalent.

Question 2.
Identify the properties used to determine if the expressions are equivalent.
A. 4(a + 2b) + 4a and 8(a + b)
4(a + 2b) + 4a = 4a + 8b + 4a __________ Property
= 4a + 4a + 8b _____________ Property of Addition
= (4 + 4)a + 8b _____________ Property
= ()a + 8b Add inside parentheses.
= 8(a + b) ______________ Property
4(a + 2b) + 4a (is / is not) equivalent to 8(a + b).
Answer:
4(a + 2b) + 4a = 4a + 8b + 4a Associative Property
= 4a + 4a + 8b Commutative Property of Addition
= (4 + 4)a + 8b Distributive Property
= (8)a + 8b Add inside parentheses.
= 8(a + b) Distributive Property of addition
4(a + 2b) + 4a is equivalent to 8(a + b).

B. 8xy + 5xy and 3xy
8xy + 5xy = ( + )xy ____________ Property
= ()xy Add inside parentheses
8xy + 5xy (is / is not) equivalent to 3xy.
Answer:
8xy + 5xy = (8 + 5)xy Distributive Property
= (13)xy Add inside parentheses
8xy + 5xy is not equivalent to 3xy.

Question 3.
A triangle is drawn so that starting from the shortest side, each side is one unit longer. The expression s + (s + 1) + (s + 2) gives the perimeter of the triangle. Each of the s terms are like terms and can be combined.

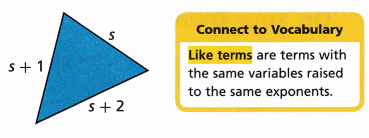
s + (s + 1) + (s + 2)
= (s + s) + 1 + (s + 2) ____________ Property of Addition
= (s + s) + (s + 2) + 1 ____________ Property of Addition
= (s + s + s) + 2 + 1 ____________ Property of Addition
= (1 + 1 + 1) + 2 + 1 ____________Property
= s + Add.
Answer:
s + (s + 1) + (s + 2)
= (s + s) + 1 + (s + 2) Associative Property of Addition
= (s + s) + (s + 2) + 1 Associative Property of Addition
= (s + s + s) + 2 + 1 Associative Property of Addition
= (1 + 1 + 1) s + 2 + 1 Distributive property
= 3s + 3 Add.

Question 4.
Are the expressions 6w + 3z + 4w + 7z and 8(w + z) equivalent?
In the expression 6w + 3z + 4w + 7z, the terms 6w and 4w are ____________, and the terms ____________ and ____________ are like terms.
6w + 3z + 4w + 7z
= 6w + 4w + 3z + 7z ____________ Property of Addition
= (6 + 4) + ( + )z ____________ Property
= w + z Add inside parentheses.
= 10( + ) ____________ Property
6w + 3z + 4w + 7z (is/is not) equivalent to 8(w + z).
Answer:
6w + 3z + 4w + 7z Commutative Property of Addition
(6 + 4) w + (3 + 7)z Distributive Property
10w + 10z Add inside parentheses.
10(w + z) Distributive Property

Turn and Talk How can you show that 8(xy + xy) is equivalent to 16xy?
Answer:
8(xy + xy) = 8(2xy) = 16xy
So, the answer is yes, the expression 8(xy + xy) is equivalent to 16xy

Check Understanding

Rewrite the first expression to determine whether the expressions are equivalent.

Question 1.
8x + 4y = ____________
8x + 4y is ____________ to 4(2x + 1).
Answer:
8x + 4y
Using the distributive property of addition
8x + 4y = 4(2x + y)
8x + 4y is not equivalent to 4(2x + 1).

Question 2.
3 (k + 3) = ____________
3(k + 3) is ____________ to 3k + 9.
Answer:
3(k + 3) = 3k + 9
3(k + 3) is equivalent to 3k + 9.

On Your Own

Question 3.
Use Structure To find the perimeter of a rectangle, you can use different expressions: l + w + l + w, 2l + 2w, or 2(l + w). Show that the expressions are equivalent.

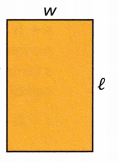
l + w + l + w = l + l + w + w ____________ Property of Addition
l + l + w + w = + Combine like terms.
2l + 2w = Distributive Property
Answer:
l + w + l + w = l + l + w + w Commutative Property of Addition
l + l + w + w = 2l + 2w Combine like terms.
2l + 2w = 2(l + w) Distributive property of addition

Question 4.
Reason Marcus wrote an expression equivalent to 7(x + 8). Liz wrote a different expression that has the same value as Marcus’ expression when x = 2. What could Liz’s expression be?
Answer:
Given,
Marcus wrote an expression equivalent to 7(x + 8).
x = 2
7(2 + 8) = 7(10) = 70

Question 5.
Critique Reasoning On a math test, students earn 4 points for each correct answer and lose 1 point for each incorrect answer. If there are 50 questions on the test, a student’s score is shown by the expression 4(50 – w) – w, where w is the number of wrong answers. Chris says that the expression 5(40 – w) could also be used. Is he correct? Why or why not? Show your work.

Answer:
Given,
Students earn 4 points for each correct answer and lose 1 point for each incorrect answer.
4(50 – w) – w = 200 – 4w – w = 200 – 5w
Simplify the expression by using the distributive property of addition.
200 – 5w = 5(40 – w)
Yes, Chris is correct.

Question 6.
What property of operations is used to show that 12x + 6y is equivalent to 6(2x + y)?
Answer:
12x + 6y
By using the distributive property of addition we can write the equivalent expression of 12x + 6y
12x + 6y = 6(2x + y)

Question 7.
Open-Ended Write an expression that is equivalent to 5(d + 2f) + 5d.
Answer:
5(d + 2f) + 5d = 5d + 10f + 5d = 10d + 10f = 10(d + f)

For Problems 8-13, combine like terms.

Question 8.
8w² – 3w² = ______________
Answer:
8w² – 3w² = w²(8 – 3) = 5w²

Question 9.
x + 5 + 7x = ______________
Answer:
x + 5 + 7x
Combine the like terms x and 7x
x + 5 + 7x =8x + 5

Question 10.
6p³ + 2p² + p³ = _____________
Answer:
6p³ + 2p² + p³
Combine the like terms.
7p³ + 2p²
Take p as common factor.
p(7p² + 2p)
6p³ + 2p² + p³ = p(7p² + 2p)

Question 11.
2(x + 4) – 5 = _______________
Answer:
2(x + 4) – 5
2x + 8 – 5
2x + 3
2(x + 4) – 5 = 2x + 3

Question 12.
g + 3 + 4(g + 2) = _____________
Answer:
g + 3 + 4(g + 2)
g + 3 + 4g + 8
5g + 11
g + 3 + 4(g + 2) = 5g + 11

Question 13.
3(x² + 2) + 8 = _______________
Answer:
3(x² + 2) + 8
Multiply the parentheses expression with 3.
3x² + 6 + 8 = 3x² + 14

Question 14.
Construct Arguments Determine whether 6y + 18 + 3y is equivalent to 9(y + 2). Use properties of operations to justify your answer.
Answer:
6y + 18 + 3y = 9y + 18
By using the distributive property of addition we can simplify the expression.
6y + 18 + 3y = 9y + 18 = 9(y + 2).

Question 15.
6(4x + 3y) and 3(8x + 6y) are equivalent expressions. Explain why this is true.
Answer:
6(4x + 3y) = 24x + 18y
3(8x + 6y) = 24x + 18y
Yes, both the expressions are equivalent.

Question 16.
Sarah earns $7.50 per hour babysitting and $5.00 per hour walking dogs. Last week she worked h hours babysitting and twice as many hours walking dogs. Write an expression to show the amount of money Sarah earned last week. Then multiply and combine like terms to write the expression as one term.

Answer:
Given,
Sarah earns $7.50 per hour babysitting and $5.00 per hour walking dogs.
Last week she worked h hours babysitting and twice as many hours walking dogs.
The expression is 7.50h + 2h(5)
= 7.50h + 10h = 17.5h

Question 17.
Reason If 2n is added to an expression, it will be equivalent to 6(2n + 3). For which expression is this true:
12n + 21, 10 + 9, 2(5n + 9), or 12n + 1? Show how you know.
Answer:
Given,
If 2n is added to an expression, it will be equivalent to 6(2n + 3).
We have to check whether the given expressions are equivalent to 6(2n + 3)
12n + 21 = 3(4n + 7) + 2n = 14n + 21 ≠ 6(2n + 3)
10 + 9 ≠ 6(2n + 3)
2(5n + 9) = 10n + 18 + 2n = 12n + 18 = 6(2n + 3)
12n + 1 + 2n = 14n + 1 ≠ 6(2n + 3)
So, the expression 2(5n + 9) is true.

Question 18.
Determine whether the expressions 6x + 2 + 4x and 8x + 4 have the same value when x = 2.
6x + 2 + 4x is equal to when x = 2.
8x + 4 is equal to when x = 2.
Do 6x + 2 + 4x and 8x + 4 have the same value when x = 2?
Answer:
6x + 2 + 4x
when x = 2
6(2) + 2 + 4(2) = 12 + 2 + 8 = 22
8x + 4 = 8(2) + 4 = 22
6x + 2 + 4x is equal to 22 when x = 2.
8x + 4 is equal to 22 when x = 2.
Yes 6x + 2 + 4x and 8x + 4 have the same value when x = 2.

Question 19.
Identify the property used in each step.
6x + (19 + 5x) = 6x + (5x + 19) ____________ Property of Addition
= (6x + 5x) + 19 _____________ Property of Addition
= 11x + 19
Answer:
6x + (19 + 5x) = 6x + (5x + 19) Associative Property of Addition
The associative property of addition states that when adding more than two numbers, the grouping of the numbers doesn’t change the sum.
= (6x + 5x) + 19 Associative Property of Addition
6x + (19 + 5x) = 11x + 19
6x + (5x + 19) = 11x + 19
(6x + 5x) + 19 = 11x + 19
6x + (19 + 5x) = 6x + (5x + 19) = (6x + 5x) + 19 = 11x + 19

For Problems 20-21, determine if the expressions are equivalent.

Question 20.
4m + 3m is ______________ to 7m.
Answer:
4m + 3m
The above expression is the like terms so we can combine the numbers.
4m + 3m = 7m
So, 4m + 3m is equivalent to 7m.

Question 21.
3j + 3k is ______________ to \(\frac{1}{4}\)(8j + 12k)
Answer:
\(\frac{1}{4}\)(8j + 12k) = 2j + 3k
So, 3j + 3k is not equivalent to \(\frac{1}{4}\)(8j + 12k).

Question 22.
Which expression is NOT equivalent to the others? Explain.
12p + 8
6p + 8 + 6p
4(p + 2) + 3p
4(3p + 2)
Answer:
12p + 8
We can write it as 6p + 6p + 8 = 12p + 8
12p + 8 = 4(3p + 2) = 12p + 8
4(p + 2) + 3p = 4p + 8 + 3p = 7p + 8
Therefore 12 + 8 is not equivalent to 4(p + 2) + 3p.

Question 23.
A rectangle is 4 units wide and 6 + x units long. Write two expressions to represent the area of the rectangle.
Answer:
Given,
A rectangle is 4 units wide and 6 + x units long.
Width = 4 units
Length = 6 + x units
We know that,
Area of a rectangle = l × w
A = (6 + x) × 4
A = 24 + 4x
Thus the area of the rectangle is 4x + 24

Question 24.
Open-Ended Each weekday, Ana runs in the morning and the afternoon. Write an expression to show how long Ana runs for any number of days d. Then multiply and combine like terms to write the expression as one term.

Answer:
Given,
Each weekday, Ana runs in the morning and the afternoon.
Ana runs 3/4 hour in the morning.
Ana runs 1/2 hour in the afternoon.
We have to add the total time run in the morning and afternoon and multiply it by the total days.
The expression would be D(3/4 + 1/2).

Question 25.
Use Structure Determine if the expressions 4x and 3x + 3 have the same value when x = 3 and when x = O.
4x = when x = 3. 3x + 3 = when x = 3.
4x = when x = 0. 3x + 3 = when x = 0.
The expressions have the same value when x = , but not when x = .
This means that 4x and 3x + 3 ______________ equivalent expressions.
Answer:
4x
when x = 3
4(3) = 12
4x
when x = 0
4(0) = 0
3x + 3
when x = 3
3(3) + 3 = 9 + 3 = 12
when x = 0
3(0) + 3 = 3
4x = 12 when x = 3. 3x + 3 = 12 when x = 3.
4x = 0 when x = 0. 3x + 3 = 3 when x = 0.
The expressions have the same value when x = 3, but not when x = 0.

For Problems 26-31, find an equivalent expression using the Distributive Property.

Question 26.
25w + 30x
Answer:
25w + 30x
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
Take 5 as a common multiple to write the equivalent expression.
25w + 30x = 5(5w + 6x)

Question 27.
x(4 + y)
Answer:
x(4 + y)
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
x(4 + y) = 4x + 4y

Question 28.
0.25(8r – 4m)
Answer:
0.25(8r – 4m)
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
0.25 × 8r – 0.25 × 4m
2r – 1m
0.25(8r – 4m) = 2r – m

Question 29.
24 + 8k
Answer:
24 + 8k
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
Take 8 as a common number to simplify the expression.
24 + 8k = 8(3 + k)

Question 30.
4xy – 16x
Answer:
4xy – 16x
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
Take 4x as a common factor to simplify the expression.
4xy – 16x = 4x(y – 4)

Question 31.
g³(7 + h)
Answer:
g³(7 + h)
The distributive property is multiplying a number by a sum or difference is the same as multiplying by each number in the sum or difference and then adding or subtracting.
g³(7 + h) = 7g³ + 7h

For Problems 32-33, determine if the expressions are equivalent.

Question 32.
7(x + 4) is _____________ to 7x + 4.
Answer:
7(x + 4) = (7 × x) + (7 × 4) = 7x + 28
7(x + 4) is not equivalent to 7x + 4.

Question 33.
3r + 11 + 5r is _____________ to 2(4r + 3) + 5.
Answer:
2(4r + 3) + 5
8r + 6 + 5 = 8r + 11 = 3r + 11 + 5r
3r + 11 + 5r is equivalent to 2(4r + 3) + 5.

Lesson 8.5 More Practice/Homework

Question 1.
Use Tools A pattern of squares is shown. It changes by the same amount in each step. Kwan has determined that he can use the expression 2(n + 1) – 3 to find the number of squares for any step number n. Find an equivalent expression that Kwan also can use.

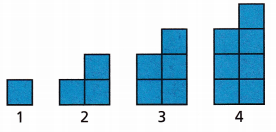
Answer:
2(n + 1) – 3
⇒ 2n + 2 – 3
⇒ 2n – 1
Thus the equivalent expression is 2n – 1.

Question 2.
Determine if the expressions have the same value when x = 5
6x + 9 and 3(2x + 3)
The value of 6x + 9 when x = 5 is .
The value of 3(2x + 3) when x = 5 is .
Do 6x + 9 and 3(2x + 3) have the same value when x = 5?
Answer:
The value of 6x + 9 when x = 5 is
6(5) + 9 = 30 + 9 = 39
3(2x + 3) = 3(2(5) + 3) = 3(10 + 3) = 3(13) = 39
Thus 6x + 9 and 3(2x + 3) have the same value when x = 5.

Question 3.
Critique Reasoning Trisha says that since 4(3s + 2) and 5(7s – 3) both equal 20 when s = 1, the expressions are equivalent. Is she correct? Explain.
Answer:
4(3s + 2)
s = 1
4(3(1) + 2) = 4(3 + 2) = 4(5) = 20
5(7s – 3)
s = 1
5(7(1) – 3) = 5(7 – 3) = 5(4) = 20
Hence Trisha is correct.

Question 4.
A stained glass sun catcher in the shape of a pentagon is shown. Write and simplify an expression to find the perimeter of the pentagon in inches.

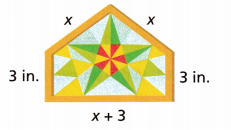
Answer:
The perimeter of a pentagon is the sum of all the 5 sides.
a = x in.
b = x in.
c = 3 in.
d = x + 3 in.
e = 3 in.
P = a + b + c + d + e
P = x + x + 3 + x + 3 + 3
P = 3x + 9
P = 3(x + 3)
Thus the perimeter of the pentagon is 3(x + 3) inches.

Question 5.
The surface area of a rectangular prism with length l, width w, and height h is given by the expression 2lw + 2lh + 2wh. Write an equivalent expression using the Distributive Property.
Answer:
The surface area of a rectangular prism with length l, width w, and height h is given by the expression 2lw + 2lh + 2wh.
By using Distributive Property we can write the equivalent expression.
2lw + 2lh + 2wh = 2(lw + lh + wh)

Math on the Spot For Problems 6-7, identify the property.

Question 6.
3(6 • 5) = (3 • 6)5 ________________ Property of Multiplication
Answer:
Associative Property of Multiplication: When multiplying more than two numbers, the grouping of the numbers does not change the product.
3(6 • 5) = (3 • 6)5
In this case the product is same for both the numbers.
3 (6 × 5) = 3 × 30 = 90
(3 × 6) × 5 = 18 × 5 = 90

Question 7.
w + z = z + w ________________ Property of Addition
Answer:
w + z = z + w is Commutative property of addition.
Definition: Commutative property of addition states that when adding the numbers or expressions, changing the order of the numbers does not change the sum.

For Problems 8-9, determine whether the expressions are equivalent.

Question 8.
6r + 3w – 2r + 5w is _______________ to 4(r + 2w).
Answer:
6r + 3w – 2r + 5w
6r – 2r + 3w + 5w
4r + 8w
Let us take 4 as a common factor.
4(r + 2w)
So, 6r + 3w – 2r + 5w is equivalent to 4(r + 2w).

Question 9.
12d + 8r is ______________ to 2(5d + 4r) + 4d.
Answer:
2(5d + 4r) + 4d
10d + 8r + 4d
10d + 4d + 8r
14d + 8r
So, 12d + 8r is not equivalent to 2(5d + 4r) + 4d.

Test Prep

Question 10.
What property of operations can be used to justify that the two expressions in this equation are equivalent? 6x² + 4x = 4x + 6x²
Answer:
The commutative property of operations is used to justify that the two expressions in this equation are equivalent.
6x² + 4x = 4x + 6x²
x(6x + 4) = x(4 + 6x)
The order of the equation is different but the equation is the same.

Question 11.
Do the expressions 6x – 4x and 12x ÷ 6 have the same value when x = 6?
6x – 4x = when x = 6. 12x ÷ 6 = when x = 6.
The expressions 6x – 4x and 12x ÷ 6 (do / do not) have the same value when x = 6.
Answer:
6x – 4x
x = 6
6x – 4x = 2x
2(6) = 12
12x ÷ 6
x = 6
12(6) ÷ 6 = 12
Thus expressions 6x – 4x and 12x ÷ 6 have the same value when x = 6.

Question 12.
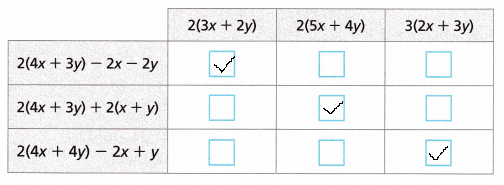
Fill in the box in the column of the expression that is equivalent to each expression on the side of the chart.

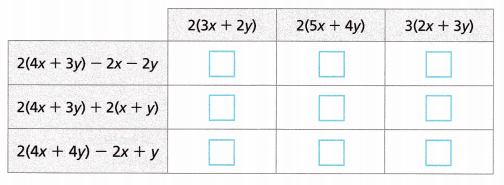
Answer:
2(4x + 3y) – 2x – 2y
8x + 6y – 2x – 2y
8x – 2x + 6y – 2y
6x + 4y
Taking 2 as the common factor
It becomes 2(3x + 2y)
2(4x + 3y) + (2x + 2y)
8x + 6y + 2x + 2y
10x + 8y
Taking 2 as the common factor
It becomes 2(5x + 4y)
2(4x + 4y) – 2x + y
8x + 8y – 2x + y
8x – 2x + 8y + y
6x + 9y
Taking 3 as the common factor
It becomes 3(2x + 3y)

Question 13.
Which expressions are equivalent to 6(h + 4)? Select all that apply.
(A) 6h + 4
(B) 6h + 24
(C) h + 10
(D) 4(h + 4) + 2(h + 4)
(E) 2(3h + 12)
Answer:
Given,
6(h + 4)
It can be written as 6h + 24
Take 2 as common factor
It becomes 2(3h + 12)
(D) 4(h + 4) + 2(h + 4) = 4h + 16 + 2h + 8
= 6h + 24
Thus Option B, D and E are the correct answers.

Question 14.
Write an expression that is equivalent to 24x + 36y.
Answer:
Given expression 24x + 36y
We can simplify by taking 6 as the common factor.
6(4x + 6y)
or
We can simplify by taking 12 as the common factor.
12(2x + 3y)
So, the expression that is equivalent to 24x + 36y is 12(2x + 3y).

Spiral Review

Question 15.
Penny is 100 centimeters tall. Jeremy is 38 inches tall. Who is taller? Show how you know. [Note: 1 centimeter ≈ 0.394 inches]
Answer:
Penny is 100 centimeters tall.
Jeremy is 38 inches tall.
1 centimeter ≈ 0.394 inches
100 × 0.394 = 39.4 inches
39.4 inches is greater than 38
So, Penny is taller than Jeremy.

Question 16.
What integer is the opposite of 12?
Answer: The integer opposite of 12 is -12.

Question 17.
Write 5 × 5 × 5 × 5 × 5 × 5 × 5 as an expression with an exponent.
Answer: 5 × 5 × 5 × 5 × 5 × 5 × 5 = 5⁷