We included HMH Into Math Grade 6 Answer Key PDF Module 8 Lesson 3 Write Algebraic Expressions to Model Situations to make students experts in learning maths.
HMH Into Math Grade 6 Module 8 Lesson 3 Answer Key Write Algebraic Expressions to Model Situations
I Can use variables to write an algebraic expression to represent a real-world problem.
Spark Your Learning
Viola is helping to plant a rectangular community garden. A plant handbook states that 1 plant requires 8 square inches of soil. Given the dimensions of the rectangular garden shown, how many plants can be planted in the garden? Explain.


Answer:
We know that area of rectangle = l x b
First, find out the area of the rectangle.
area = 24 x 84
area = 2016 square inches.
The above-given question was that 1 plant needs 8 square inches of soil.
Now we need to know the number of plants that can be planted in the garden. Let it be X.
X = 2016/8
X = 252 plants.
Therefore, Viola can plant 252 plants in the garden.
Turn and Talk If the width of the garden were increased to 36 inches, how many more plants could be put in the garden? Explain.
Answer:
Already we know the width in the above-given diagram.
The width is 24 inches. But here the width is increased to 36 inches. So add the inches. Let it be X.
X = 24 + 36
X = 60.
and the length is constant which is 84 inches.
Now find out the area of the rectangle.
area = 60 x 84
area = 5040
Now we have to find out the number of plants she can plant in the garden after an increase in the width.
Let it be P.
P = 5040/8 [ 1 plant needs 8 square inches of soil.]
P = 630
Therefore, she can plant 630 plants in the garden.
Build Understanding
An algebraic expression is an expression that contains one or more variables.
A variable is a letter or symbol used to represent one or more unknown quantities.
A constant is a specific number whose value does not change.
Connect to Vocabulary
A coefficient is the number that is multiplied by the variable in an algebraic expression.
2x + 75 is an example of an algebraic expression.
2 is a coefficient.
x is a variable.
75 is a constant.
Question 1.
A day-care centre has 2 baskets of dolls. One basket has 8 dolls, and the other basket has an unknown number of dolls in it. What expression can you use to represent this situation?
A. Can you write a numerical expression to represent this situation? Explain.
Answer:
We cannot write numeric expressions here because we don’t know the number of dolls present in the second box. So we can represent an unknown number of dolls as X which is variable.
The total number of baskets of dolls = 2
The number of dolls in one basket = 8
The number of dolls in another basket = X.
B. What do you know about this situation? Complete the sentences.
There are ![]() baskets. One has
baskets. One has ![]() dolls in it.
dolls in it.
The other basket has ____________ number of dolls.
Answer:
There are 2 baskets.
One has 8 dolls in it.
The other basket has X number of dolls.
We don’t the number of dolls in the other basket so we represented X.
C. If you do not have all the information you need, could you still write an expression to represent this situation? Explain.
Answer:
Yes, we can write an expression
These expressions are represented with the help of unknown variables, constants and coefficients. The combination of these three (as terms) is said to be an expression. It is to be noted that, unlike the algebraic expression, an algebraic expression has no sides or is equal to a sign. Some of its examples include X – 30.
D. Complete the bar model to represent this situation. Then write an expression to represent the bar model.
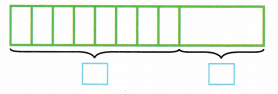
The expression is ![]() +
+ ![]() .
.
Answer:
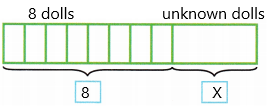
The expression is (x + 8)
8 is a constant
X is a variable.
A variable is an unknown quantity which we need to evaluate by solving the given algebraic equation.
E. Explain why the expression in Part D is an algebraic expression. Identify the coefficient.
Answer:
An algebraic expression is a combination of constants, variables and algebraic operations (+, -, ×, ÷). We can derive the algebraic expression for a given situation or condition by using these combinations.
Here 1 is the coefficient of x.
According to the properties of the coefficient:
A variable without a number has 1 as its coefficient. In the expression X + 8, 1 is the coefficient.
Turn and Talk Suppose the number of dolls in both baskets is unknown. Write an expression for the number of dolls. Do the variables you choose to make a difference? Explain.
Answer:
Yes, we can choose different variables to make a difference.
For suppose, the dolls present in the first box be X.
The dolls present in the second box be Y.
The expression would be: X + Y
Question 2.
Kristen works at a supermarket. She wants to divide a box of apples equally among 3 displays.

A. Let f represent the total number of apples. Complete the bar model to express the number of apples each display will have.
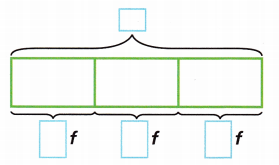
Answer:
B. Write an algebraic expression that represents the number of apples each display will have. Write your answer as a product and a quotient.
Answer:
C. Kristen decides to use an additional 12 apples for each display. What is the new algebraic expression that represents the number of apples each display will have?
Answer:
Turn and Talk How would the algebraic expression change if, instead of putting an additional 12 apples in each display, Kristen decided to keep 6 apples from the total number before she divided them among the 3 displays? Explain.
Answer:
Check Understanding
Question 1.
Raj is 3 inches taller than Howard. Let h represent Howard’s height. Write an algebraic expression to represent Raj’s height.
Answer:
The height of Howard = h
The number of inches Raj is taller than Howard = 3
The algebraic expression represents Raj’s height as h + 3.
therefore, the raj’s height = h + 3
Question 2.
Marcus has 4 times the sum of 6 and the number of marbles David has. Let d represent the number of marbles David has. Write an algebraic expression to represent how many marbles Marcus has.
answer:
The number of marbles is d.
The expression to represent the number of marbles Marcus has: 4d + 6
4 is a coefficient
d is the variable
6 is the constant.
For Problems 3-4, write an algebraic expression for the words. Identify the coefficient(s).
Question 3.
the quotient of t and 13
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is: t/13
Question 4.
the product of g and 2 plus m
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is: g(2 + m)
On Your Own
Question 5.
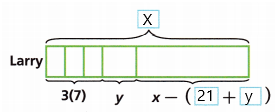
Use Tools Larry and Zach have both been hired to do odd jobs. Larry will receive $7 for each of the 3 flower beds he weeds and y dollars to edge a yard. Zach will receive $25 to clean out a garage and y dollars to wash a car. Both Larry and Zach need to make x dollars to meet their goal. Write an expression for the amount each still has to earn to reach his goal.
A. Complete the model to show the amount of money Larry needs.
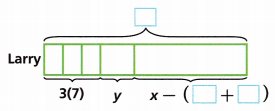
Answer:
The amount Larry receives = $7
The number of flower beds he weeds = 3
The number of dollars to edge a yard = y
The total amount is X.
The expression is X – (21 + y)
B. Complete the model to show the amount of money Zach needs.
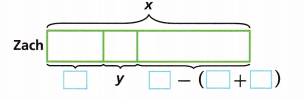
Answer:
The amount Zach receives for cleaning a garage = $25
The amount he receive was a car = y
The total amount is X.
The expression is X – (25 + y)
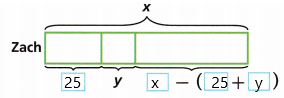
C. Reason Who has more money left to earn before meeting his goal? Explain.
Answer:
The Zach: X – (25 + y)
The Lary: X – (21 + y)
Zach has more money because if he cleans out one garage he could get $25 and Lary should weed 3 flower beds to get $21. Compared to both Zach is having more money.
Question 6.
Jayden begins with 25 cups of soil at the greenhouse. Each day he will fill 5 cups more. Write an algebraic expression to represent the number of cups he will have after n days. Identify the coefficient.

Answer:
The number of cups of soil Jayden begins at the greenhouse = 25
The number of cups he fills each day = 5
The algebraic expression represents the number of cups he will have after n days.
The expression be: 5n + 25
5 is the coefficient.
For Problems 7-9, write an algebraic expression for the word expression.
Question 7.
32 divided by b
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is: 32/b
Question 8.
the sum of 112 and m
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is: 112 + m
Question 9.
the product of \(\frac{1}{2}\) and x
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is: 1/2 * x
I’m in a Learning Mindset!
What about writing algebraic expressions triggers a fixed-mindset voice in my head?
Answer:
Lesson 8.3 More Practice/Homework
Question 1.
Financial Literacy Clyde rents a tuxedo for several days. Let d represent the number of additional days Clyde uses the tuxedo. Write an algebraic expression to represent the total cost of the rental after d additional days.

Answer:
The number of additional days = d
The expression represents the total cost of the rental after d additional days.
The expression be: 10d + 75
d is a variable
10 is the coefficient
75 is a constant.
Question 2.
Math on the Spot Sage and Tom started the month with the same number of talk minutes on their cell phone plans. Sage talked for 7 minutes with her dad. Tom talked for 4 minutes with a friend and for 3 minutes with his mom. Do Sage and Tom have the same number of talk minutes left on their cell phone plans?
A. Complete the models to represent Sage’s and Tom’s minutes. Then write an algebraic expression to represent the number of minutes each has left.
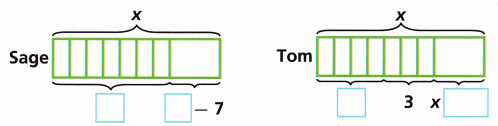
Answer:
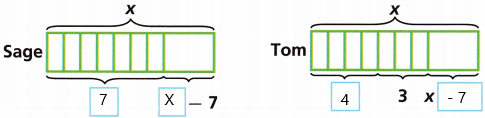
The number of minutes Sage will talk to his dad = 7
The total number of minutes is X.
The algebraic expression represents the number of minutes talk on cell phone
The expression is X – 7
The number of minutes a Tom talks to his friend = 4
The number of minutes a tom talks to his mom = 3
The minutes he talks to his mom and friend = 4 + 3 =7
The total number of minutes is X.
The algebraic expression represents the number of minutes talk on a cell phone
The expression is X – 7
Now we have to write an algebraic expression to represent the number of minutes each has left.
The expression: (X – 7) + (X – 7)
B. Do Sage and Tom have the same number of talk minutes left on their cell phone plans? Explain your reasoning.
Answer:
Yes, they both talked for the same number of minutes because the same expressions are also the same X – 7.
Question 3.
Open-Ended Nola fits together p pieces a day of a 5,000-piece puzzle. Write an algebraic expression for this situation and explain what it represents.
Answer:
The number of pieces Nola fits a puzzle = P
The number of puzzle pieces = 5000
The algebraic expression: P – 5000
For Problems 4-5, write an algebraic expression for the word expression.
Question 4.
the product of 7, and c minus 13
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is:
7c – 13
Question 5.
the quotient of 10 times m and 7
Answer:
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The basics of algebra taught us how to express an unknown value using letters such as x, y, z, etc. These letters are called here variables. An algebraic expression can be a combination of both variables and constants. Any value that is placed before and multiplied by a variable is a coefficient.
The expression for the above phrase is:
10m/7.
Identify the variable. coefficient, and constant term of the expression.
Question 6.
4b + 24
variable: _____________
coefficient: _____________
constant: _____________
Answer:
An algebraic expression in mathematics is an expression which is made up of variables and constants, along with algebraic operations (addition, subtraction, etc.). Expressions are made up of terms.
These expressions are represented with the help of unknown variables, constants and coefficients. The combination of these three (as terms) is said to be an expression. It is to be noted that, unlike the algebraic equation, an algebraic expression has no sides or is equal to a sign.
The above-given expression: 4b + 24
b is a variable.
4 is a coefficient
24 is a constant.
Question 7.
11y + 4.5
variable: _____________
coefficient: _____________
constant: _____________
Answer:
An algebraic expression in mathematics is an expression which is made up of variables and constants, along with algebraic operations (addition, subtraction, etc.). Expressions are made up of terms.
These expressions are represented with the help of unknown variables, constants and coefficients. The combination of these three (as terms) is said to be an expression. It is to be noted that, unlike the algebraic equation, an algebraic expression has no sides or is equal to a sign.
The above-given equation is 11y + 4.5
y is a variable
11 is a coefficient
4.5 is a constant.
Test Prep
Question 8.
Alix has x dollars per week available for lunch. She spends $3 on lunch every weekday. Write an algebraic expression to represent how much money she has leftover at the end of the week.
Answer:
The amount Alix has for lunch per week = X
The amount she spends on lunch everyday = $3
The algebraic expression represents how much money she has leftover at the end of the week. Let it be L.
In a week there are 7 days.
L = X – 3(7)
L = X – 21
Question 9.
The Color My Room painting company charges a fixed set-up fee of $20 per job and then $0.25 per square foot to paint. Let p represent the square footage of a laundry room’s walls. Write an algebraic expression to find the total cost to paint the room.
Answer:
Since there is a set-up fee of $20 then you would have to add it to the value of what 0.25p will be. Since p represents every square foot of the walls and you would multiply p by 0.25 every square foot is $0.25 then 0.25p+20.
Therefore, the total cost to paint the room is 0.25p + 20.
Question 10.
A farmer gathered eggs from his chickens. Let e represent the total number of eggs he collected. He gives a third of the eggs to his friend, 7 of the eggs to another friend, and the rest to his cousin. Select all the algebraic expressions that represent the number of eggs he gives to his cousin.
(A) \(\frac{1}{3}\)e + 7
(B) e – \(\frac{1}{3}\)e – 7
(C) e – \(\frac{e}{3}\) – 7
(D) \(\frac{e}{3}\) – 7
Answer: Option B and C are correct.
The total number of eggs he collected = e
The number of eggs he gives to his friend = 1/3
The number of eggs he had given to his other friend was 7 and the rest of the eggs were given to his cousin.
The expression will be:
e – (1/3 + 7)
e – [1/3] -7
Question 11.
Let g represent the total number of hours Greg will travel on his trip across the country to attend his cousin’s wedding. The first day he travels 8 hours. The second day he travels 9 hours. The third day he had mechanical problems and only drove for 4 hours. Write an algebraic expression to represent how much time he has left to drive.
Answer:
The total number of hours Greg travelled = g
The number of hours he travelled for the first day = 8
The number of hours he travelled for the second day = 9
The number of hours he travelled for the third day = 4
We need to write the algebraic expression to represent how much time he has left to drive. Let the equation be E.
E = g – (8 + 9 + 4)
E = g – 21.
Therefore, the algebraic expression is g-21.
Spiral Review
Question 12.
What is 75% of 128?
Answer:
To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100.
Percentage formula = (Value/Total value) × 100
How to calculate the percentage of a number:
To calculate the percentage of a number, we need to use a different formula such as:
P% of Number = X
where X is the required percentage.
If we remove the % sign, then we need to express the above formulas as;
P/100 * Number = X
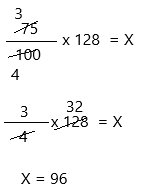
Question 13.
What is 2,220 yards in miles? Round to the nearest tenth of a mile. [Note: 1 mile = 1,760 yards]
Answer:
Already given that 1 mile = 1760 yards.
2220 yards = M miles.
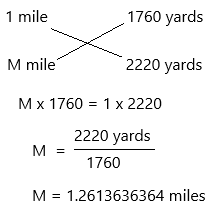
The nearest tenth value is 1.3
Question 14.
Haru is putting lace around the edge of a rectangular pillowcase that has a length of 12.75 inches and a width of 15.5 inches. How much lace does he need?
Answer:
The perimeter of a rectangle: A four-sided polygon having two dimensions i.e. length and breadth is called a rectangle. The total distance covered by the boundaries or the sides in the case of the rectangle is known as the perimeter of a rectangle.
Formula:
The perimeter of a rectangle is the measure of the sum of its all sides which in the case of a rectangle are four sides in total. The perimeter, for any polygon, is defined as the total distance covered by its sides. Since the opposite sides in a rectangle have equal lengths and widths, the perimeter of the rectangle is twice the length of the rectangle plus twice the width of the rectangle.
Perimeter of rectangle formula = 2 × (length + width)
In the above-given:
length is 12.75 inches; width is 15.5 inches.
Perimeter of lace = 2 ( 12.75 + 15.5 )
Perimeter of lace = 2 ( 28.25 )
Perimeter of lace = 56.5
Therefore, Haru needs 56.5 inches of lace.