We included HMH Into Math Grade 6 Answer Key PDF Module 8 Lesson 2 Write and Evaluate Numerical Expressions for Situations to make students experts in learning maths.
HMH Into Math Grade 6 Module 8 Lesson 2 Answer Key Write and Evaluate Numerical Expressions for Situations
I Can write and evaluate numerical expressions using the order of operations.
Spark Your Learning
Two tour groups are visiting an aquarium. There are 20 children in one group and 22 children in the other. Along with the 2 group leaders, there are 5 additional adults between the two groups. If the cost per child is $9.00 and the total for both groups is $490, what is the cost per adult? Explain your reasoning.

Answer:
The children in one group = 20
The children in another group = 22
The number of group leaders = 2
The number of additional adults = 5
The total number of adults = group leaders + additional adults (5 + 2 = 7)
The cost per child = $9.00
The total cost for both groups = $490
The cost per adult = A
The total cost for children of two groups = (20 x 9) + (22 x 9) = 180 + 198 = 378
We already know the total cost of both groups. So we can easily find out the individual cost of an adult.
The total cost of adults in both groups = X
x = 490 – 378
X = 112
Now divide the 112 and the total adults.
A = 112/7
A = 16
Therefore, the cost per adult is $16.
Turn and Talk If the aquarium gave both groups a 10% discount, what would the total cost be? Explain.
Answer:
We know that the total cost is $490
If the aquarium 10% discount then the total cost be X.
X = 490 x 10/100
X = $49
Build Understanding
The parts of an expression that are added or subtracted are called terms.
Connect to Vocabulary
A numerical expression is an expression that contains only numbers and operations. 7 + 8 × 22, 25 – 16 + 9 are examples of numerical expressions.
Question 1.
Consider the expressions in Parts A-D.
A. How many terms does the expression 14 + 9 have? What are they? Explain how you know.
Answer:
There are two terms 14 and 9.
14 + 9 is the numeric expression.
A numeric expression consists of numbers and operations, but never includes any variable. Some of the examples of numeric expressions are 10 + 9, 14 ÷ 2, etc.
In that expression the symbols are operators and the numbers are called like terms.
B. How many terms does the expression 6 + 20 – 9 have? What are they? Explain how you know.
answer:
There are 3 terms. Those are 6, 20, and 9
6+20-9 is also a numeric expression.
A numeric expression consists of numbers and operations, but never includes any variable. Some of the examples of numeric expressions are 10 + 9, 14 ÷ 2, etc.
In that expression the symbols are operators and the numbers are called like terms.
‘+’ and ‘-‘ are the operating symbols.
C. The expression 25 + (4 × 5) has _________ terms, namely __________, because it is a ___________ of those expressions.

The expression 4 × 5 has two __________, namely __________, because it is a __________ of those expressions.
Answer:
The expression 25 + (4 × 5) has 3 terms, namely 25, 4 and 5 because it is a sum of those expressions.
The expression 4 x 5 has two terms, namely 4 and 5. Because it is a product of those expressions.
D. The expression \(\frac{7}{10}\) – \(\frac{11}{20}\) has _________ terms, namely, _________and _________, because it is a __________ of those expressions.
The fraction expression \(\frac{7}{10}\) is also a _____________ because it represents 7 __________ 10.
Answer:
The above-given expression has two terms namely, 7/10 and 11/20. Because it is a difference between those expressions.
The fraction 7/10 is also division because it represents 7 ÷ 10.
Question 3.
How can you write a numerical expression to represent a phrase?
A. Consider the phrase, “the product of 7 and the sum of 5 and 4.”
The sum of 5 and 4 is written as ___________.
The product of 7 and the sum of 5 and 4 is written as _____________.
Answer:
A numeric expression consists of numbers and operations, but never includes any variable.
The sum of 5 and 4 can be written as 5 + 4
The product of 7 and the sum of 5 and 4 can be written as 7 x (5 + 4)
B. Consider the phrase, “the square of the difference of 9 and 3.”
The difference of 9 and 3 is written as __________.
The square of the difference of 9 and 3 is written as _____________.
Answer:
The difference between 9 and 3 is written as 9 – 3
The square of the difference can be written as: (9 – 3)2
It was like the square of the difference between two expressions: (a – b)2 = a2 – 2ab + b2
Turn and Talk Compare and explain the meanings of 23 and 2(3).
Answer:
2^3 means 2 x 2 x 2 = 8
2(3) = 6
2(3) is a multiplication form.
Multiplication is the process of calculating the product of two or more numbers. The multiplication of numbers say, ‘a’ and ‘b’, is stated as ‘a multiplied by ‘b’.
2^3 is an exponential form.
To write numbers in exponential form, we need to express them raised to certain powers of their prime factors as shown in the following examples:
8 = 2 × 2 × 2 = 23. Therefore, the exponential form of 8 can be expressed as 2^3.
Step It Out
You learned about the order of operations in a previous grade. Now we need to add exponents into our order of operations. Exponents are calculated after performing operations in parentheses or brackets.
Connect to Vocabulary
Evaluate means to find the value of a numerical or algebraic expression.
Question 3.
The correct order of operations has been used to evaluate the given expressions. Identify the operation used in each step.
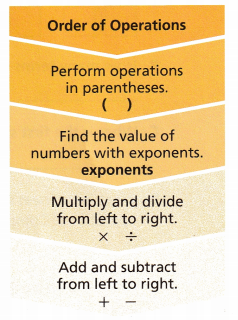
A. 33 + 12 × 2
27 + 12 × 2 Evaluate exponents.
27 + 24
51
Answer:
By following the PEMDAS order of operation:
Step 1:
First, calculated exponents: 3^3 = 3 x 3 x 3 = 27
27 is substituted in the place of 3^3.
27 + 12 x 2
Step 2:
Multiply and divide (left to right): 12 x 2 = 24
Now substitute the 24 in the place of 12 x 2
27 + 24
Step 3:
Add and subtract (left to right): 27 + 24 = 51.
This is the order followed in the above-given question.
B. 72 ÷ (15 – 6) + 3 × 22
72 ÷ 9 + 3 × 22
72 ÷ 9 + 3 × 4
8 + 3 × 4
8 + 12
20
Answer:
By following PEMDAS order of operations:
Step 1:
Firstly, calculated within the parentheses (15 – 6) = 9
Now substitute the value in the place of parentheses.
72 ÷ 9 + 3 × 2^2
Step 2:
Now calculated the exponents: 2^2 = 4
Now the equation is: 72 ÷ 9 + 3 × 4
Step 3:
Multiply and divide (left to right): 72 ÷ 9 = 8
8 + 3 x 4
Step 4:
Multiply and divide (left to right): 3 x 4 = 12
8 + 12
Step 5:
Add and subtract (left to right): 8 + 12 = 20.
C. 15 + 32 – 6 + (5 + 2)2
15 + 32 – 6 + 72
15 + 32 – 6 + 49
47 – 6 + 49
41 + 49
90
Answer:
By following the PEMDAS order of operations:
Step 1:
Firstly, calculated within the parentheses: 5 + 2 = 7
15 + 32 – 6 + 7^2
Step 2:
Next, calculated exponents: 7^2 = 49
15 + 32 – 6 + 49
Step 3:
Add and subtract (left to right):
15 + 32 – 6 + 49 = 90
Turn and Talk
Why is it important to follow the order of operations?
Answer:
– The order of operations is a group of rules that tells you the right order in which to solve different parts of a math problem.
– You should follow the order of operations because you need to get an accurate result. If these rules concerning order of operations would no exist, then each solver will solve an algebra in a particular way and it is less probable to come to a correct answer.
Question 4.
A staff member is buying beds for all the dogs in a shelter. There are 10 dogs in one building and 14 dogs in another building. The price of a bed
is shown.

A. Complete the numerical expression to find the total cost.
![]()
Answer:
The number of dogs in one building = 10
the number of dogs in other buildings = 14
The cost of the bed is $12
To find the total cost we need to write a numeric expression. Let it be D.
D = 12 ( 10 + 14) [ numeric expression].
B. How many terms are there in the parentheses?
Answer:
There are two terms in the parentheses. Namely, 10 and 14.
C. What is the first step for evaluating this expression? Complete the step.
Answer:
By following the PEMDAS order of operation:
The first step will be:
Calculate the numbers within the parentheses:
10 + 14 = 24
D. What is the next step for evaluating the expression using the order of operations? Complete the step.
Answer:
After calculating the parentheses, the next step is:
Multiply and divide (left to right):
12 ( 24)
= 288
E. Use the Distributive Property to evaluate 12(10 + 14) and show it is equal to your previous evaluation.
Answer:
Distributive property: The distributive property is the one which allows us to multiply the number by a group of numbers, which are added together. The distributive property is given by: a(b+c) = ab + ac
Given expression: 12(10+ 14)
We know that the distributive property is given by:
a(b+c) = ab+ ac
Hence,
12(10 + 14) = 12(10) + 12(14)
=120 + 168
= 288
Therefore, 12 (10+14) is 288
The previous calculation is equal to distribution property evaluation.
F. What is the total cost of the beds?
Answer:
The total cost of beds = 12 ( 10 + 12)
= 12 ( 24 )
= 288
Therefore, the cost of a bed is $288
Check Understanding
Question 1.
Consider the expression 20 – (42 ÷ 2). How many terms does it have? Identify them. Also identify a quotient in the expression.
Answer:
The above-given expression: 20 – (42 ÷ 2)
Follow the PEMDAS order of operations:
Step 1:
Calculate within the parentheses:
(42 ÷ 2) = (16 ÷ 2) = 8
The quotient is 8.
Step 2:
Add and subtract (left to right):
= 20 – 8
= 12
Question 2.
Write a numerical expression to represent the phrase “the quotient of 12 and the product of 4 and 5”.
Answer:
The above-given phrase: the quotient of 12 and the product of 4 and 5
First, create an expression. Since it says “the product of”, we know that 4 and 5 should be in parenthesis and are multiplied. “The quotient of” means that 12 is being divided by the product of 4 and 5.
Our expression is 12/(4*5).
Now, solve; 4 times 5 is 20, so now we have 12/20. 12 divided by 20 is 0.6
Question 3.
Use the order of operations to evaluate the expression.
4(7 + 9) + 82 – 7 ___________
Answer:
By following the PEMDAS order of operation:
Step 1:
Calculate within the parentheses (7 + 9 ) = 16
4 x 16 + 82 – 7
Step 2:
Now calculate the exponents: 8^2 = 64
Now substitute the 64 in the place of 8^2.
4 x 16 + 64 – 7
Step 3:
Multiply and divide (left to right): 4 x 16 = 64
Now put 64 in the place of 4 x 16.
64 + 64 – 7
Step 4:
Add and subtract (left to right):
64 + 64 – 7 = 121.
Therefore, the answer for the expression: 4(7 + 9) + 82 – 7 = 121.
On Your Own
Question 4.
Lamar drinks 8 ounces of water with breakfast, 6 ounces of water with his vitamins, 16 ounces of water with his lunch, 16 ounces of water with his dinner, and 32 ounces of water from a bottle he carries throughout the day. Write and evaluate a numerical expression for the amount of water in ounces that he drinks in a week.
Answer:
The amount of water in ounces he drinks in a week = X
Add all the ounces of water that he takes with the above-given things.
X = 8 + 6 + 16 + 16 + 32
X = 78
Therefore, he takes 78 ounces of water in a week.
Question 5.
Use Structure Kyle rides his bicycle to school 5 days a week. He also rides from school to the soccer field twice a week. Every day, he rides his bicycle home on the same paths. Write and evaluate a numerical expression for the total number of miles Kyle bikes during the week.
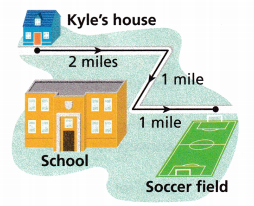
A. Write an expression for the number of miles Kyle rides his bike on a day when he does not go to the soccer field.
Answer:
The distance from Kyle house to school = 2 +1 =3 miles.
Kyle rides his bicycle 5 days a week. Then the total miles in a week = 5 x 3 = 15 miles.
The distance from school to soccer field = 1mile
Kyle rides his bicycle 2 days a week = 2 x 1 = 2 miles.
The expression for the number of miles Kyle rides his bike on a day when he does not go to the soccer field = X
X = 2 + 1
X = 3 miles.
B. Write an expression for the number of miles Kyle bikes on a day when he does go to the soccer field.
Answer:
If he goes to the soccer field from school then the expression will be 3 + 1 = 4 miles.
from house to school the miles are 3.
from school to the soccer field the miles are 1.
by adding both the miles we get the total miles in a day.
C. Write and evaluate an expression for the total number of miles Kyle bikes during the week.
Answer:
The distance from Kyle house to school = 2 +1 =3 miles.
Kyle rides his bicycle 5 days a week. Then the total miles in a week = 5 x 3 = 15 miles.
The distance from school to soccer field = 1mile
Kyle rides his bicycle 2 days a week = 2 x 1 = 2 miles.
Now add the total miles from home to school and school to soccer field. Let the answer be X.
X = 15 + 2
X = 17
Therefore, he rides 17 miles in a week.
For Problems 6-9, evaluate each expression.
Question 6.
25 – 21 ÷ 3 = ___________
Answer:
By following the PEMDAS order of operation:
Step 1:
Multiply and divide (left to right):
21 ÷ 3 = 7
Step 2:
Add and subtract (left to right):
25 – 7 = 18
Therefore, the answer for the above-given expression is 18.
Question 7.
8 + 8 ÷ 8 = _____________
Answer:
By following the PEMDAS order of operation:
Step 1:
Multiply and divide (left to right):
8 ÷ 8 = 1
Step 2:
Add and subtract (left to right):
8 + 1 = 9
Therefore, the answer for the above-given expression is 9
Question 8.
10 – 4 × 1 + 7 = ______________
Answer:
By following the PEMDAS order of operation:
Step 1:
Multiply and divide (left to right):
4 x 1 = 4
Step 2:
Add and subtract (left to right):
10 – 4 + 7 = 13
Therefore, the answer for the above-given expression is 13.
Question 9.
18 ÷ 3 – 1 × 4 = ___________
Answer:
By following the PEMDAS order of operation:
Step 1:
Multiply and divide (left to right):
18 ÷ 3 = 6
Step 2:
Multiply and divide (left to right):
1 x 4 = 4
Step 3:
Add and subtract (left to right):
6 – 4 = 2
Therefore, the answer for the above-given expression is 2.
For Problems 10-11, complete the sentence using sum, difference, product, quotient, or factors.
Question 10.
The expression 20 + (8 ÷ 2) is the ___________ of 20 and (8 ÷ 2). The expression 8 ÷ 2 is the __________ of 8 and 2.
Answer:
The expression 20 + (8 ÷ 2) is the sum of 20 and (8 ÷ 2). The expression 8 ÷ 2 is the quotient of 8 and 2
Question 11.
The expression 11 × 6 has two ___________, namely 11 and 6, because it is the ___________ of those expressions.
Answer:
The expression 11 × 6 has two factors, namely 11 and 6, because it is the product of those expressions.
For Problems 12-15, write a numerical expression to represent the phrase.
Question 12.
the sum of 6 and the square of 12 _________________
Answer:
This can be written in expression as:
6 + 12^2.
This can be solved by applying the PEMDAS order of operation:
First, calculate the exponent:
12^2 = 12 x 12 = 144
And now add:
6 + 144 = 150.
Question 13.
the quotient of 30 and the sum of 5 and 7 _________________
Answer:
The above-given phrase: the quotient of 30 and the product of 5 and 7
First, create an expression. Since it says “the sum of”, we know that 5 and 7 should be in parenthesis and are added. “The quotient of” means that 30 is being divided by the sum of 5 and 7.
Our expression is 12/(5+7).
Now, solve; 12/12 = 1
Question 14.
the difference of 4 cubed and 25 _________________
Answer:
This phrase can be written as: 4^3 – 25
4^3 = 4 x 4 x 4 = 64
64 – 25 = 39
Question 15.
5 more than the product of 12 and 8 _________________
Answer:
This phrase can be written as: (12 x 8) + 5
product of 12 and 8 is 12 x 8
by following the PEMDAS order of operations:
First, calculate within the parentheses
12 x 8 = 96
Now add the 5.
96 + 5 = 101.
Question 16.
Critique Reasoning Aman and Jennifer both evaluated the same numerical expression. They got different answers. Who simplified the expression correctly? Explain.

Answer:
Jennifer simplified the expression correctly.
Explanation:
Jennifer followed the PEMDAS order of operations so she got the answer correct.
In the PEMDAS rule, firstly, she calculated the exponent.
3^2 = 9
1 + 4 . 9
Next multiply : 4. 9 = 36
Now add 1 + 36 = 37.
Question 17.
Use Repeated Reasoning A field has 11 dandelions. Complete the statements by writing numerical expressions to show the total number of dandelions after 1 month, 2 months, 3 months, and 4 months. Use exponents in your answers for Part A.

A. After 1 month, there are 11 • ![]() dandelions
dandelions
After 2 months, there are 11 • ![]() dandelions
dandelions
After 3 months, there are __________ dandelions.
After 4 months, there are __________ dandelions.
Answer:
After 1 month, there are 11. 11 = 121 dandelions
After 2 months, there are 11. 11 = 1331 dandelions.
After 3 months, there are 11. 11^3 = 14641 dandelions.
After 4 months, there are 161051 dandelions.
B. Evaluate the last expression in Part A. Show your work.
Answer:
The last expression in part A:
After 4 months, there are 161051 dandelions.
We know the 3rd month has 14641 dandelions. As said every month it doubles.
11. 11^4 = 161051 dandelions.
For Problems 18-21, evaluate the expression.
Question 18.
7 + 15 ÷ 3 • 2 – 12 ___________
Answer:
Follow PEMDAS order of operations:
Multiply and divide: 15 ÷ 3 • 2 = 10
7 + 10 – 12
Add and subtract: 7 + 10 – 12 = 5
Therefore, the answer for the above-given expression is 5.
Question 19.
6(9 – 6) – 23 + 4 _____________
Answer:
Follow PEMDAS order of operations:
Step 1:
First, calculate within the parentheses:
(9 – 6) = 3
6(3) – 2^3 + 4
Step 2:
Calculate exponents:
2 ^3 = 8
6(3) – 8 + 4
Step 3:
Now multiply: 6. 3 = 18
18 – 8 + 4
Step 4: Now add and subtract:
18 – 8 + 4 = 14
Therefore, the answer for the above-given expression is 14.
Question 20.
(7 – 6) + 9 – 2 • 5 _____________
Answer:
Follow PEMDAS order of operations:
Step 1:
First, calculate within the parentheses:
(7 – 6) = 1
1 + 9 – 2 . 5
Step 2:
Now multiply: 2. 5 = 10
1 + 9 – 10
Step 3:
Now add and subtract:
10 – 10 = 0
Therefore, the answer for the above-given expression is 0.
Question 21.
7 + (2 – 1)5 • 8 ______________
Answer:
Follow PEMDAS order of operations:
Step 1:
First, calculate within the parentheses:
( 2 – 1 ) = 1
7 + (1)^5 . 8
Step 2:
Calculate exponents:
(1)^5 = 1
7 + 1 . 8
Step 3: Multiply
7 + 8
Step 4: add
7 + 8 = 15.
Therefore, the answer for the above-given expression is 15.
I’m in a Learning Mindset!
How did I apply prior knowledge to evaluate numerical expressions using order of operations?
Answer:
You can do that with many different subjects. You have able to know how to use symbols to express numbers, operations, and variables. It is a very complex process. It involves the use of numbers, variables, and operators to solve specific problems.
The most common mathematical procedures are addition, subtraction, division, multiplication and then solving for variables.
Lesson 8.2 More Practice/Homework
Question 1.
STEM Margarite is building 3 prototypes of a robot she designed. Each robot includes a body and a remote control. She needs 450 inches of wire for each body and 120 inches for each remote control. In addition, she is going to build one master remote to run all three robots at once. The master remote will require 380 inches of wire. Write and evaluate a numerical expression to find the total length of wire she will need.
A. Write an expression for the amount of wire needed for a robot.
Answer:
The number of prototypes of a robot designed by Margarite = 3
Each body needs 450 inches of wire
Each remote control needs 120 inches of wire.
Now we need to write the expression for the amount of wire needed for a robot.
The expression is: 450 + 120
B. Write an expression for the total amount of wire needed for all 3 robots.
Answer:
The number of prototypes of a robot designed by Margarite = 3
Each body needs 450 inches of wire
Each remote control needs 120 inches of wire.
Now we need to write the expression for the amount of wire needed for all 3 robots.
The expression is: 3(450 + 120)
C. Write an expression for the amount of wire needed for all 3 robots and the master remote.
Answer:
The number of prototypes of a robot designed by Margarite = 3
Each remote control needs 120 inches of wire.
Each master remote needs 380 inches of wire.
Now we need to write the expression for the amount of wire needed for all 3 robots and the master remote:
The expression is : 3(120 + 380)
D. How much wire will Margarite need to complete her project?
Answer:
The number of prototypes of a robot designed by Margarite = 3
Each body needs 450 inches of wire
Each remote control needs 120 inches of wire.
Each master remote needs 380 inches of wire
To complete her 3 prototypes of robots which is her complete project and she needs the total wire be X.
Now add all the inches of wire and multiply with 3.
X = 3 ( 450 + 120 + 380 )
Apply the PEMDAS rule:
First, calculate within the parentheses
X = 3(950)
Now multiply:
X = 2850
Therefore, she needs 2850 inches of wire to complete her project.
Question 2.
For a company picnic, Todd fills 30 paper cups with ketchup and Yuki fills 27 paper cups with ketchup. Each paper cup holds 1 ounce. Later, Todd and Yuki learn that two other company employees completed exactly the same task. How many ounces of ketchup did the four employees prepare?
Answer:
The number of paper cups filled with ketchup by Todd = 30
The number of paper cups filled with ketchup by Yuki = 27
The number of ounces each paper cup holds = 1
Likewise, the other two did the same task = 30 + 27 = 57.
The Todd holds 30 x 1 = 30 ounces.
The Yuki holds 27 x 1 = 27 ounces.
The two employees hold 57 x 1 = 57 ounces.
Now add all these ounces. Let the answer be X.
X = 30 + 27 + 57
X = 114.
Therefore, the four employees hold 114 ounces of ketchup.
Question 3.
Reason At football practice on Monday, Brandon threw a football into the target 5 times. The next Monday, he tripled the number of targets he hit. On the following Monday, his hits doubled that of the week before. Write and evaluate a numerical expression to find how many times he hit the target during those three weeks.

Answer:
On the first Monday, he hits 5 times.
On the second Monday, he hits a triple of 5 which is 5^3
On the third Monday, he hits doubled of 5 which is 5^2.
The numeric expression is: X
X = 5 + 5^3 + 5^2
Now evaluating the expression:
By following the PEMDAS order of operations:
Step 1: Now calculate the exponents.
5^3 = 5 x 5 x 5 = 125
5^2 = 5 x 5 = 25
5 + 125 + 25
Step 2: Add
5 + 125 + 25 = 155.
Therefore, he hits 155 times during that three weeks.
Math on the Spot For Problems 4-7, evaluate each expression.
Question 4.
25 – 21 ÷ 3
Answer:
By following the PEMDAS order of operation:
Step 1:
Divide: 21 ÷ 3 = 7
25 – 7
Step 2:
Subtract: 25 – 7 = 18
Therefore, the answer for the above-given expression is 18.
Question 5.
50 + 12 ÷ 3 × 5 – 2
Answer:
By following the PEMDAS order of operation:
Step 1: Multiply and divide
12 ÷ 3 × 5 = 20
Step 2: add and subtract
50 + 20 – 2
= 70 – 2
= 68
Therefore, the answer for the above-given expression is 68.
Question 6.
7 + 33 × 10
Answer:
By following the PEMDAS order of operation:
Step 1: calculate the exponent
3^3 = 3 x 3 x 3 = 27
Step 2: multiply
7 + 27 x 10
= 7 +270
Step 3: add
277.
Therefore, the answer for the above-given expression is 277.
Question 7.
40 – 42 × 2 + 1
Answer:
By following the PEMDAS order of operation:
Step 1: calculate the exponent.
4^2 = 4 x 4 = 16
Step 2: multiply
40 – 16 x 2 + 1
40 – 32 + 1
Step 3: add and subtract.
40 – 32 + 1 = 9.
Therefore, the answer for the above-given expression is 9.
Test Prep
Question 8.
Evaluate the expression.
13 – 2 × 5 + 72
(A) 104
(B) 594
(C) 100
(D) 52
Answer: Option D is correct.
Follow the PEMDAS order of operations:
First, we have to calculate exponents:
7^2 = 49
= 13 – 2 x 5 + 49
Multiply and divide (left to right):
2 x 5 = 10
= 13 – 10 + 49
Add and subtract (left to right):
= 3 + 49
= 52
Question 9.
Mr. Kershner is a school nurse. He uses, on average, 24 self-adhesive bandages during each spring month: March, April, and May. He also knows that in June there are several field days and he will need 4 times the number of bandages for that month. How many bandages should he order for March through June? If the bandages cost 3 cents each, what is his total cost for March through June?
Answer:
The number of self-adhesive bandages is needed during march = 24
The number of self-adhesive bandages is needed during April = 24
The number of self-adhesive bandages is needed during May = 24
The number of self-adhesive bandages is needed during June = 24 x 4 = 96
The total cents a nurse invested in march = 24 x 3 = 72
The total cents a nurse invested in April = 24 x 3 = 72
The total cents a nurse invested in May = 24 x 3 = 72
The total cents a nurse invested in June = 96 x 3 = 288
The total a nurse invested on bandages through march to June = X
X = 72 + 72 + 72 + 288
X = 504
Therefore, the total cost is 504 cents.
Question 10.
To evaluate the expression, what is the first step to follow?
2(7 + 3 ÷ 3 × 7)2 – 100
(A) Divide 3 ÷ 3.
(B) Multiply 3 × 7.
(C) Multiply by 2.
(D) Add 7 + 3.
Answer: Option B is correct.
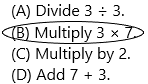
According to the PEMDAS order of operations:
First, we need to calculate within the parentheses:
In parentheses, there are addition, multiplication and division operations are there.
In that, we need to calculate the multiplication order and then division lastly addition.
Question 11.
Evaluate 15 × 3 + 7(4 + 1) – 52. What is the second step according to order of operations?
Answer:
Follow the PEMDAS order of operations:
Step 1: Calculate with in the parentheses
(4 + 1) = 5
15 x 3 + 7(5) – 5^2
Step 2: Calculate the exponents:
5^2 = 5 x 5 = 25
15 x 3 + 7(5) – 25
Step 3: Multiply
15 x 3 + 7(5) – 25
45 + 35 – 25
Step 4: add and subtract.
45 + 35 – 25
55
Therefore, the answer for the above-given expression is 55.
According to the question, the second step we need to calculate is exponents.
Spiral Review
Question 12.
What is 30% of 400?
Answer:
To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100.
Percentage formula = (Value/Total value) × 100
How to calculate the percentage of a number:
To calculate the percentage of a number, we need to use a different formula such as:
P% of Number = X
where X is the required percentage.
If we remove the % sign, then we need to express the above formulas as;
P/100 * Number = X
The above-given problem is:
30% of 400 is:
= 30/100 x 400
= 120.
Question 13.
In a circle graph displaying the most popular fruit sold to students in the school cafeteria, the ratio of apples to the total pieces of fruit sold is \(\frac{3}{5}\). What is the angle measure of the apple section of the graph?
Answer:
Question 14.
On the last history test, Kim scored 80% and Juan answered 27 out of 30 questions correctly. Who answered more questions correctly?
Answer:
The total number of questions = 30
The number of answers scored correctly by Juan = 27
The percentage of Kim = 80%
Actually, Juan answered more questions correctly.
Kim answered 24 questions correctly.
80% of 30 questions.
80/100 x 30 = 24.
Therefore, Kim answered 24 questions correctly and Juan answered 27 questions correctly.