Into Math Grade 6 Module 7 Lesson 1 Answer Key Understand, Express, and Compare Percent Ratios

We included HMH Into Math Grade 6 Answer Key PDF Module 7 Lesson 1 Understand, Express, and Compare Percent Ratios to make students experts in learning maths.

HMH Into Math Grade 6 Module 7 Lesson 1 Answer Key Understand, Express, and Compare Percent Ratios

I Can convert ratios to percents by applying one strategy.

Spark Your Learning
A race car uses 2 gallons of gas to travel 25 miles. How many miles can the race car travel on 8 gallons of gas?

Answer:

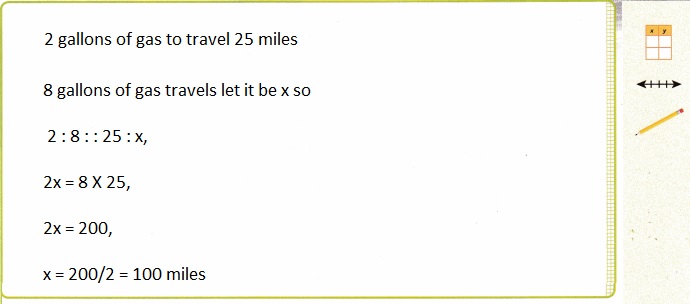
100 miles the race car travel on 8 gallons of gas,

Explanation:
Given a race car uses 2 gallons of gas to travel 25 miles.
Number of miles can the race car travel on 8 gallons of gas is as ratios it is 2: 8 :: 25 : x, 2x = 8 X 25, 2x = 200, so x = 200/2  = 100 miles.

Turn and Talk How can you use the ratio of 2 gallons of gas to 25 miles to write a ratio for the number of miles the race car travels on 1 gallon of gas? How could this be useful?
Answer:
2 : 1 :: 25 : x,

Explanation:
Using 2 gallons of gas to 25 miles only we can write a ratio for the number of miles the race car travels on 1 gallon of gas if it is x so the ratio is 2 : 1 :: 25 : x, As a  ratio is a comparison of two or more numbers that indicates their sizes in relation to each other. A ratio compares two quantities by division, with the dividend or number being divided termed the antecedent and the divisor or number that is dividing termed the consequent.

Build Understanding

1. Eleanor, Tillie, and Caleb earn money training dogs to surf. For every dollar they earn, Caleb gets 20 cents, Tillie gets 30 cents, and Eleanor gets 50 cents.

Connect to Vocabulary
A percent is a ratio that compares a number to 100. It is represented by the percent symbol, %.

A. Write a ratio that shows how much each trainer earns from a dollar.
Caleb: : 100
Tillie: : 100
Eleanor: : 100
Answer:
Caleb: 20 : 100, Tillie:  30 : 100, Eleanor: 50 : 100,

Explaantion:
Given Eleanor, Tillie, and Caleb earn money training dogs to surf.
For every dollar they earn, Caleb gets 20 cents, Tillie gets 30 cents and Eleanor gets 50 cents.
Ratio showing how much each trainer earns from a dollar is Caleb: 20 : 100,
Tillie:  30 : 100, Eleanor: 50 : 100.

B. Caleb’s portion of each dollar earned is shaded on the 10 × 10 grid. How many boxes do you need to shade to represent Tillie’s portion? Shade in Tillie’s portion of each dollar on the grid.

Answer:

Explanation:
Boxes do I need to shade to represent Tillie’s portion is 30,
Shaded in Tillie’s portion of each dollar on the grid as shown above.

C. A percent is a part-to-whole ratio with a whole of 100. You can write 25% as 25 : 100 or \(\frac{25}{100}\) Write percents to represent the amounts Caleb and Tillie earn from each dollar. Explain how you found them.
__________________________
__________________________
__________________________
__________________________
Answer:
Caleb : 20 : 100 or \(\frac{20}{100}\), Tillie : 30 : 100 or \(\frac{30}{100}\),

Explanation:
Given Tillie and Caleb earn money training dogs to surf.
For every dollar they earn, Caleb gets 20 cents, Tillie gets 30 cents,
Therefore the percents to represent the amounts Caleb and Tillie earn from each dollar is
Caleb : 20 : 100 or \(\frac{20}{100}\), Tillie : 30 : 100 or \(\frac{30}{100}\).

D. What does the part of the grid that isn’t shaded represent? Write a percent to represent this portion of the grid.
__________________________
__________________________
__________________________
Answer:
If 50% is used means out 100 only 50 boxes are shaded that part is utilized represents out of 100,
50 are used rest 100-50 = 50 boxes are not used and its percent is 50%.

Turn and Talk Devon says that the ratios 2:10, 3:10, and 5:10 represent Caleb’s, Tulle’s, and Eleanor’s portions. Is Devon right? If so, explain how he found these ratios, If not, explain Devon’s error.
Answer:
Yes Devon is right,

Explanation:
Given Devon says that the ratios 2:10, 3:10, and 5:10 represent Caleb’s, Tulle’s, and Eleanor’s portions. Yes Devon is right he divided the portions of ratios and took out common factors and
gave the remaining rest result.

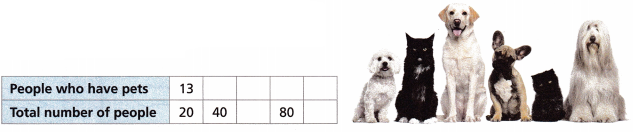
2. A survey says that 13 out of 20 people have pets. Write this ratio as a percent.

A. One way to write a ratio as a percent is to use a table. Complete the table to write equivalent ratios for the ratio 13:20.

Answer:

Explanation:
Completed the table to write equivalent ratios for the ratio 13:20 as shown above.

B. Use the table to write the percent of people who own pets. What is \(\frac{13}{20}\) as a percent? Explain.
Answer:
65%,

Explanation:
The percent for \(\frac{13}{20}\) X 100 = 65%.

C. You also can use equivalent ratios to find the percent. What is \(\frac{13}{20}\) as a percent?

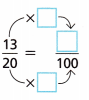
Answer:

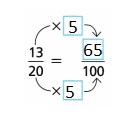
65%,

Explanation:
\(\frac{13}{20}\) as a percent is 65%.

Turn and Talk Could you use any of the ratios in the table to find the percent?
Answer:
13:20, 26:40, 39:60, 52:80 and 65 : 100 all have 65%,

Explanation:
Yes, I can use the ratios in the table to find the percent as all ratios 13:20, 26:40, 39:60, 52:80 and 65 : 100 have 65%, If \(\frac{13}{20}\) X 100 = 65%, \(\frac{26}{40}\) x 100 = 65%,
\(\frac{39}{60}\) X 100 = 65%, \(\frac{52}{80}\) X 100 = 65%,
\(\frac{65}{100}\) X 100 = 65%.

3. A recipe for pie crust includes the ingredients shown. Find the ratio of sugar to flour as a percent.

A. What fraction can represent the ratio of sugar to flour? Convert this fraction to a decimal. Explain how you did the conversion.
__________________________
__________________________
Answer:
1:4, Fraction to a decimal is 0.25,

Explaantion:
The fraction that represent the ratio of sugar to flour is \(\frac{1}{4}\) the ratio is 1:4, So this fraction to decimal is \(\frac{1}{4}\) = 0.25.

B. Write the decimal as a percent. Explain how you found the percent.
___________________
Answer:
25%,

Explanation:
The decimal as a percent is 0.25 X 100 = 25%.

Step It Out

4. The diagram shows quiz results in red for John and Vince. Who received the higher score, John or Vince?

A. What can you do to solve this problem?
__________________________
__________________________
Answer:
Calculate John percentage and compare,

Explanation:
We calculate or find John’s percentage and compare with Vince.

B. Many test scores are written as percents. Use the double number line to convert John’s score to a percent. John’s score is a ratio with a whole of 25. So the 25 is placed with the 100% on the double number line.

To convert John’s score to a percent, what number do you mark on the top number line? ________
What number do you mark on the bottom number line? ________
Answer:

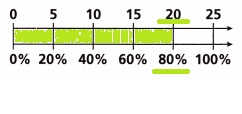
20, 80%,

Explanation:
To convert John’s score to a percent, The number do I mark on the top number line is 20,
The number do you mark on the bottom number line is 80%.

C. Use your answers in Part B to write \(\frac{20}{25}\) as a percent.

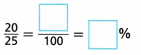
Answer:

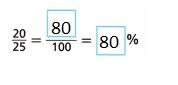
Explanation:
Used my answers in part B to write \(\frac{20}{25}\) as a percent is 80%.

D. Who received the higher score?
__________________
Answer:
Vince,

Explanation:
Vince received the higher score 82.5%.

Turn and Talk How else could you find out who had the higher score?
Answer:
Comparing decimals of John and Vince,

Explanation:
As John scored \(\frac{20}{25}\) we get  0.8 and Vince received 82.5% we divide by 100 to get decimal as \(\frac{82.5}{100}\) = 0.825 now comparing decimals 0.825 > 0.8 so Vince scored higher.

Check Understanding

Question 1.
A basketball player made 12 out of the 30 shots she attempted. What percent of shots did the basketball
player make? Explain.

Answer:
40%,

Explanation:
Given a basketball player made 12 out of the 30 shots she attempted. The percent of shots did the basketball player make are \(\frac{12}{30}\) X 100 = 40%.

For Problems 2—7. write each ratio as a percent.

Question 2.
1 to 20 _____
Answer:
5%,

Explanation:
Given to find the percent of 1 to 20 is \(\frac{1}{20}\) X 100 = 5%.

Question 3.
\(\frac{45}{75}\) _______
Answer:
60%,

Explanation:
Given to find the percent of \(\frac{45}{75}\) is \(\frac{45}{75}\) X 100 = 60%.

Question 4.
160 : 400 _____
Answer:
40%,

Explanation:
Given to find the percent of 160 to 400 is \(\frac{160}{400}\) X 100 = 40%.

Question 5.
\(\frac{12}{60}\) ________
Answer:
20%,

Explanation:
Given to find the percent of \(\frac{12}{60}\) is \(\frac{12}{60}\) X 100 = 20%.

Question 6.
5 to 250 ____
Answer:
2%,

Explanation:
Given to find the percent of 5 to 250 is \(\frac{5}{250}\) X 100 = 2%.

Question 7.
\(\frac{1}{8}\) ________
Answer:
12.5%,

Explanation:
Given to find the percent of \(\frac{1}{8}\) is \(\frac{1}{8}\) X 100 = 12.5%.

On Your Own

Question 8.
Rachel hits one home run every 40 times she bats.
A. Complete the table to write equivalent ratios for the ratio 1:40.


Answer:

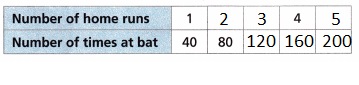
Explanation:
Completed the table to write equivalent ratios for the ratio 1:40 as shown above.

B. Use the table to write the percent of the time Rachel hits a home run after 200 times at bat.
__________________
Answer:
2.5%,

Explanation:
The percent of the time Rachel hits a home run after 200 times at bat is \(\frac{5}{200}\) X 100 = 2.5%.

Question 9.
Financial Literacy Compared to the money he made last year, Zach made 115% as much this year. Use the 10-by-10 grids to show 115%.

Did he make more or less money than last year?
Answer:

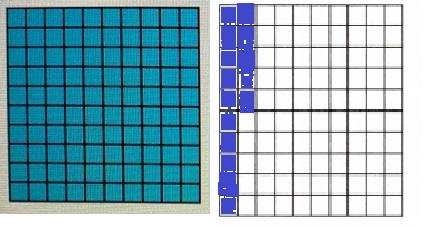
Explanation:
Given Zach made 115% as much this year. Used the 10-by-10 grids to show 115% above.

Question 10.
Construct Arguments Ryan got 36 out of 40 questions right on a test. Tessa got 92% on the same test. Who got a better score? Explain.
Answer:
Tessa got a better score,

Explanation:
Given Ryan got 36 out of 40 questions right on a test.
Tessa got 92% on the same test. Better score got by Ryan \(\frac{36}{40}\) X 100 = 90%,
Now comparing 92% is more than 90%, so Tessa got better score.

Question 11.
Open Ended Write three ratios that are equivalent to 75% and three ratios that are equivalent to 100%.
__________________
Answer:
Ratios equivalent to 75% is 1. 3:4, 2. 15:20, 3. 30:40,
Ratios equivalent to 100% are 1. 10:10, 2. 20: 20, 3. 30 : 30,

Explanation:
The Ratios equivalent to 75% is when we divide \(\frac{75}{100}\) = \(\frac{3}{4}\) ,
So next is \(\frac{15}{20}\) X 100 = 75% and \(\frac{30}{40}\) X 100 =75%,
Now when \(\frac{100}{100}\)  = 1:1, So when \(\frac{20}{20}\) we get 1:1 and
\(\frac{30}{30}\) we get 1:1 therefore Ratios equivalent to 75% is 1. 3:4
2. 15:20, 3. 30:40, Ratios equivalent to 100% are 1. 10:10, 2. 20: 20, 3. 30 : 30.

For Problems 12-17, write each number as a percent.

Question 12.
\(\frac{3}{24}\) _____
Answer:
12.5%,

Explanation:
Given to find the percent of \(\frac{3}{24}\) is \(\frac{3}{24}\) X 100 = 12.5%.

Question 13.
0.95 ______
Answer:
95%,

Explanation:
Given to find the percent of 0.95 is 0.95 X 100 = 95%.

Question 14.
8.37 ____
Answer:
837%,

Explanation:
Given to find the percent of 8.37 is 8.37 X 100 = 837%.

Question 15.
6\(\frac{1}{5}\) ____
Answer:
620%,

Explanation:
Given to find the percent of 6\(\frac{1}{5}\) is \(\frac{6 X 5 + 1}{5}\) X 100 =
\(\frac{31}{5}\) X 100 = 620%.

Question 16.
\(\frac{70}{50}\) ____
Answer:
140%,

Explanation:
Given to find the percent of \(\frac{70}{50}\) is \(\frac{70}{50}\) X 100 = 140%.

Question 17.
0.340 ____
Answer:
34%,

Explanation:
Given to find the percent of 0.340 is 0.340 X 100 = 34%.

Question 18.
Ricardo threw rings over bottles in a ring-toss competition. The diagram shows the number of bottles Ricardo got rings around.

A. Write a ratio of the number of bottles with rings to the total number of bottles.
_______________________
Answer:
12:15,

Explanation:
Given Ricardo threw rings over bottles in a ring-toss competition. The diagram showed the number of bottles Ricardo got rings around. The ratio of the number of bottles with rings to the total number of bottles is 12:15.

B. Complete the double number line to show the percentage of rings that successfully landed around a bottle.

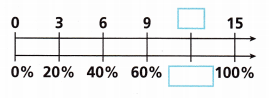
Answer:

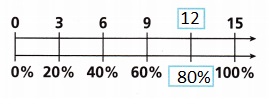
Explanation:
Completed the double number line to show the percentage of rings that successfully landed around a bottle above.

C. What percent of the bottles have rings on them? __________
Answer:
80%,

Explanation:
80% of the bottles have rings on them.

Question 19.
Two marathon runners run the full distance of the marathon, approximately 26 miles, in 4 hours.
A. About how many miles did they run in 1 hour?
_______________________
Answer:
6.5 miles,

Explanation:
Given two marathon runners run the full distance of the marathon, approximately 26 miles, in 4 hours.
About number of many miles did they run in 1 hour are \(\frac{26}{4}\) = 6.5 miles.

B. What percent of the full distance have they run in 1 hour?
_______________________
Answer:
25%,

Explanation:
Percent of the full distance have they run in 1 hour is \(\frac{6.5}{26}\) X 100 = 25%.

Question 20.
The ratio of seventh graders to sixth graders on a chess team is 5 to 3.
A. The ratio of seventh graders to total chess players is .
Answer:
5:8 or \(\frac{5}{8}\),

Explanation:
Given the ratio of seventh graders to sixth graders on a chess team is 5 to 3.
The ratio of seventh graders to total chess players is 5:8 or \(\frac{5}{8}\).

B. What percent of the players on the chess team are seventh graders? ____
Answer:
62.5%,

Explanation:
Percent of the players on the chess team are seventh graders are \(\frac{5}{8}\) X 100 = 62.5%.

Question 21.
Kari has one day each week (7-day week) to research the decline in bee populations. Approximately what percent of each week does she have to research this topic? Round your answer to the nearest hundredth of a percent. _____

Answer:
14.2% or 14%,

Explanation:
Given Kari has one day each week (7-day week) to research the decline in bee populations. Approximately the percent of each week does she have to research this topic is \(\frac{1}{7}\) X 100 = 14.2% or 14%.

I’m in Learning Mindset!

What did I learn from Task 2 that I can use in my future learning?
______________________
Answer:
Ratio’s and Percentages,

Explanation:
A ratio is a comparison of two similar quantities. Given any two similar quantities a and b, the ratio of
a to b that is a:b is defined as a:b = a/b, where b≠0. Percentage means ‘by the hundred’ or ‘divide by one hundred’. The percentage is also used to compare quantities which means ‘per 100’ I can use in my future learning.

Lesson 7.1 More Practice/Homework

Understand, Express, and Compare Percent Ratios

Question 1.
In a Louisiana chili cook-off, 18 of the 40 chilis included two types of beans. What percentage of the chilis did not include two types of beans? ____

Answer:
55%,

Explanation:
Given in a Louisiana chili cook-off, 18 of the 40 chilis included two types of beans.
Percentage of the chilis did not include two types of beans first we calculate which included two types of beans as \(\frac{18}{40}\) X 100 = 45% , So percentage of the chilis did not include two types of beans is 100% – 45% = 55% or Number of chilis did not include two types of beans are 40 -18 = 22, So percentage is \(\frac{22}{40}\) X 100 = 55%.

Question 2.
The ratio of roses to lilies in a garden is 3 to 2. If lilies and roses are the only flowers in the garden, what percentage of the garden’s flowers are roses? _____
Answer:
60%,

Explanation:
Given the ratio of roses to lilies in a garden is 3 to 2. If lilies and roses are the only flowers in the garden, The percentage of the garden’s flowers are roses \(\frac{3}{5}\) X 100 = 60%.

Question 3.
Attend to Precision The picture shows the blue and white tiles of an outdoor patio. What percent of the tiles are blue? Explain.

Answer:
36%,

Explanation:
Given the picture shows the blue and white tiles of an outdoor ratio.
The percent of the tiles are blue \(\frac{9}{25}\) X 100 = 36%.

Question 4.
A movie studio keeps 240 dresses in its wardrobe for historical films. Three-fifths of them can be used for movies that take place in the 1700s and 15% of them can be used for movies in the civil war era.

A. What percent of the dresses are for films set in the 1700s? ________
Answer:
60%

Explanation:
Given a movie studio keeps 240 dresses in its wardrobe for historical films. Three-fifths of them can
be used for movies that take place in the 1700s, Percent of the dresses are for films set in the 1700s
first we calculate number of dresses in 1700s \(\frac{3}{5}\) X 240 = 144 dresses,
Now percentage is \(\frac{144}{240}\) X 100 = 60%.

B. What percent of the dresses are for films not set in the 1700s? Explain how you found your answer.
Answer:
40%,

Explanation:
As we have percent of the dresses are for films set in the 1700s is 60%, Percent of the dresses are for films not set in the 1700s are 100% – 60% = 40%.

C. What percent of the dresses are for films set in the 1700s or during the civil war era? Explain how you found your answer.
Answer:
15%,

Explanation:
Given 15% of them can be used for movies in the civil war era. So 15% are for films set in the 1700s or during the civil war era.

D. What percent of the dresses are not for films set during the civil war era? Explain how you found your answer.
Answer:
85%,

Explanation:
As we have 15% of them can be used for movies in the civil war era, Therefore percent of the dresses are not for films set during the civil war era are 100% – 15% = 85%.

For Problems 5-8, write each number as a percent.

Question 5.
\(\frac{1}{5}\)
__________________
Answer:
20%,

Explanation:
Given to find the percent of \(\frac{1}{5}\) is \(\frac{1}{5}\) X 100 = 20%.

Question 6.
\(\frac{9}{10}\)
__________________
Answer:
90%,

Explanation:
Given to find the percent of \(\frac{9}{10}\) is \(\frac{9}{10}\) X 100 = 90%.

Question 7.
0.33
_________
Answer:
33%,

Explanation:
Given to find the percent of 0.33 is 0.33 X 100 = 33%.

Question 8.
\(\frac{11}{2}\)
__________________
Answer:
550%,

Explanation:
Given to find the percent of \(\frac{11}{2}\) is \(\frac{11}{2}\) X 100 = 550%.

Test Prep

Question 9.
A hotel puts out 3 apples for every 1 orange as the fruit for their breakfast buffet.

A. Write a ratio of apples compared to all the fruit.
________________
Answer:
3:4,

Explanation:
The ratio of apples comapred to all the fruit is 3:4.

B. What percent of the fruit in the breakfast buffet are apples?
________________
Answer:
75%,

Explanation:
Percent of the fruit in the breakfast buffet are apples is \(\frac{3}{4}\) X 100 = 75%.

Question 10.
On a necklace of 100 beads, 45 of the beads are round. The rest of the beads are rectangular. What percent of the beads are round? What percent are rectangular?
________________
Answer:
Round are 45% and Rectangular are 55%,

Explanation:
Given on a necklace of 100 beads, 45 of the beads are round.
The rest of the beads are rectangular.
The percent of the beads are round \(\frac{45}{100}\) X 100 = 45% and
The percent are rectangular are as rest beads are rectangular Rectangular beads are 100 – 45 = 55, So percent is 100% – 45% = 55% or \(\frac{55}{100}\) X 100 = 55%.

Question 11.

What percent of the tiles are vowels?
A. 25%
B. 40%
C. 60%
D. 400%
Answer:
B. 40%,

Explanation:
There are 10 tiles in that 4 tiles are vowels 2- A’s, 1 – E and 1 – O so total vowels are 4 out of 10 so percent of tiles are \(\frac{4}{10}\) X 100 = 40% matches with bit B.

Question 12.
A chorus has 50 singers. There are 16 altos and 10 tenors. What percent of the singers are altos? What percent of the singers are tenors?
A. 8%; 5%
B. 16%; 10%
C. 32%; 20%
D. 68%; 80%
Answer:
C. 32%; 20%,

Explanation:
Given a chorus has 50 singers. There are 16 altos and 10 tenors.
The percent of the singers are altos is \(\frac{16}{50}\) X 100 = 32%,
The percent of the singers are tenors is \(\frac{10}{50}\) X 100 = 20% which
matches with bit C. 32%; 20%.

Spiral Review

Question 13.
On the first move, a game piece is moved ahead two spaces. On the next move, the game piece is moved ahead five spaces. What integer represents the overall result of the two moves?
________________
Answer:
7,

Explanation:
Given on the first move, a game piece is moved ahead two spaces. On the next move, the game piece is moved ahead five spaces.The integer represents the overall result of the two moves is 2 + 5 = 7.

Question 14.
Alex paid $3.59 for 1.35 pounds of chicken. To the nearest cent, how much did Alex pay per pound?
________________
Answer:
2.66,

Explanation:
Given Alex paid $3.59 for 1.35 pounds of chicken. To the nearest cent, Alex pay per pound is
Total money divided by total weight = \(\frac{3.59}{1.35}\) = 2.659 approximately 2.66.

Question 15.
One-third of an orchestra’s musicians play violin or viola and another one-quarter play cello or contrabass. What fraction of the orchestra’s musicians play either violin, viola, cello, or contrabass?
________________
Answer:
\(\frac{7}{12}\),

Explanation:
Given one-third of an orchestra’s musicians play violin or viola and another one-quarter play cello or contrabass.
So fraction of the orchestra’s musicians play either violin, viola, cello, or contrabass are Fraction that paly violin or viola is \(\frac{1}{3}\), Fraction that play cello or contrabass is
\(\frac{1}{4}\) total is \(\frac{1}{3}\) + \(\frac{1}{4}\),
taking common denominator 12 we get \(\frac{1 X 4 + 1 X 3}{12}\) = \(\frac{7}{12}\).