We included HMH Into Math Grade 6 Answer Key PDF Module 5 Lesson 2 Represent Ratios and Rates with Tables and Graphs to make students experts in learning maths.
HMH Into Math Grade 6 Module 5 Lesson 2 Answer Key Represent Ratios and Rates with Tables and Graphs
I Can use a table or graph to find equivalent ratios and use the ratios to solve problems.
Spark Your Learning
Cameron cleans her kitchen with an eco-friendly cleaning solution. She uses 4 tablespoons of baking soda for every 1 quart of warm water. She made a table to help her mix different amounts of the cleaning solution, but the table has faded over time and some of the values are illegible. A copy of the table is shown. Complete the table and describe the strategies you used to fill in the missing quantities.

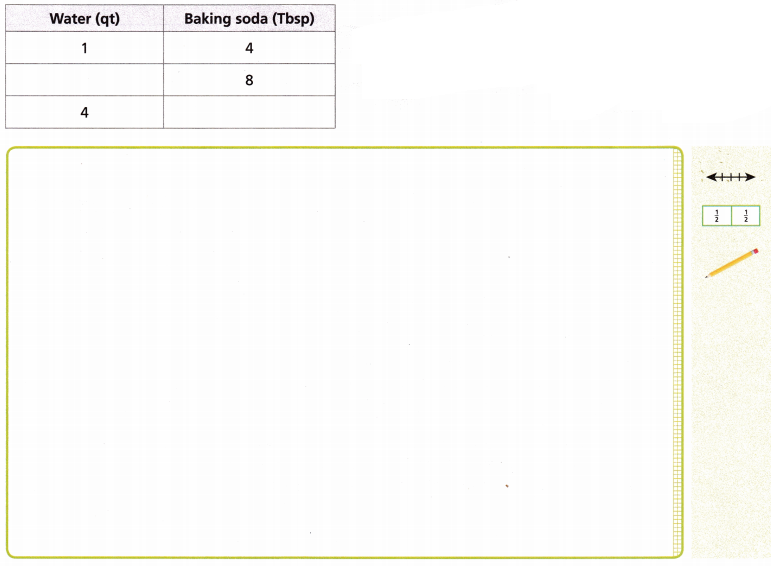
Turn and Talk What is another method you could use to complete the table.
Answer:
Build Understanding
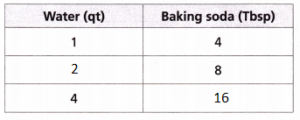
1. Hank has a recipe that calls for the ingredients shown per batch. The table shows the amount of sour cream and milk he will need if he doubles the recipe.

A. Describe a pattern you see in the amount of sour cream and the amount of milk when the recipe is doubled.
_________________
_________________
Answer:
The pattern is for 4 cups of milk we need to pour 1 sour cream.
The ratio is 1:4
B. Complete the table for 3 and 4 times the original batch size of the recipe. What did you do to find the answer?
_________________
_________________
Answer:

C. Write a ratio of cups of sour cream to cups of milk for each batch size of the recipe in the table.
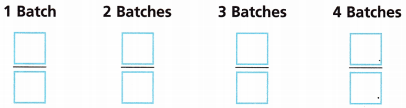
Answer:

D. Are the ratios you wrote in Part C equivalent ratios? How do you know?
Answer:
The ratio of batch 1 is 1:4
The ratio of batch 2 is 2:8 = 1:4
The ratio of batch 3 is 3:12 = 1:4
The ratio of batch 4 is 4:16 = 1:4
Thus the ratios of all 4 batches are equivalent.
Connect to Vocabulary
Equivalent ratios are ratios that name the same comparison.
E. Complete the statements.
You can ___ both terms of a ratio by the same ____ to find an equivalent ratio. So, equivalent ratios have a (multiplicative / additive) relationship.
Answer:
You can divide or multiply both terms of a ratio by the same non-zero number to find an equivalent ratio. So, equivalent ratios have a (multiplicative/additive) relationship.
F. Describe a consistent pattern between the number of cups of sour cream and the number of cups of milk. How can you use this pattern to help you find the amount of milk needed for 8 batches?
_______________________
_______________________
_______________________
Answer:
The ratio of batch 1 is 1:4
The ratio of batch 2 is 2:8 = 1:4
The ratio of batch 3 is 3:12 = 1:4
The ratio of batch 4 is 4:16 = 1:4
The ratio of batch 5 is 1 × 5: 4 × 5 = 5:20 = 1:4
The ratio of batch 6 is 1 × 6: 4 × 6 = 6:24 = 1:4
The ratio of batch 7 is 1 × 7: 4 × 7 = 7:28 = 1:4
The ratio of batch 8 is 1 × 8: 4 × 8 = 8:32 = 1:4
2. Kim takes dance classes. The dance studio offers classes in blocks.

Connect to Vocabulary
A rate is a ratio that compares two quantities that have different units.
A unit rate is a rate in which the second quantity in the comparison is one unit.
A. Kim pays $90 for every block of 5 dance classes. What rate can you write to represent this block of classes?
_______________________
Answer:
Kim pays $90 for every block of 5 dance classes.
90/5 = 18
B. Complete the diagram to find the unit rate for classes in the 5-class block. What is the cost per class?
_______________________
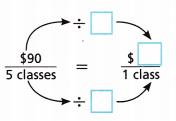
Answer:
Kim pays $90 for every block of 5 dance classes.
The cost per class = x
5 = 90
1 = x
x × 5 = 90
x = 90/5
x = 18
Thus the cost of 1 book is $18.
C. Explain in words what you did to find the cost per class in Part B.
_______________________
Answer:
Given that,
Kim pays $90 for every block of 5 dance classes.
We are asked to find the cost per class.
By applying the cross multiplication we can find the cost per class.
Thus the cost of 1 book is $18.
D. Complete the diagram to find the unit rate for classes in the 8-class block. What is the cost per class?
_________________
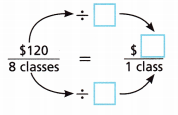
Answer:
120/8 classes = x/1 class
120 × 1 = x × 8
120 = 8x
x = 120/8
x = 15
Thus the cost per class is $15.
E. Draw your own diagram to find the cost per class in the 10-class block. What is the cost per class?
Answer:
140/10 = x/1
x × 10 = 140
x = 140/10
x = 14
The cost per class is $14.
F. Compare the unit rates you found for the blocks of classes.
___________________________
___________________________
___________________________
___________________________
Answer:
The unit rate for classes in the 5-class block is 18.
The unit rate for classes in the 8-class block is 15.
The cost per class in the 10-class block is 14.
Compared to all three classes the cost per class in the 10-class block is less than 5th class and 8th class.
Turn and Talk Describe the difference between a ratio and a rate. Is a ratio always a rate? Is a rate always a ratio? Explain.
Step It Out
3. Tovah earns money pet sitting for friends and neighbors. She earns the same amount per hour.
A. Complete the table to show how much Tovah earns for different numbers of hours.

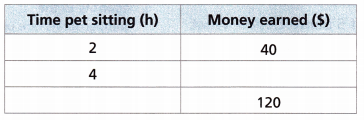
Answer:
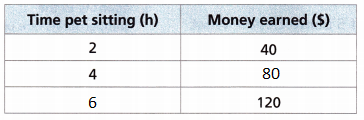
B. Graph the data from the table.
C. What do you notice about the points on the graph?
_______________________
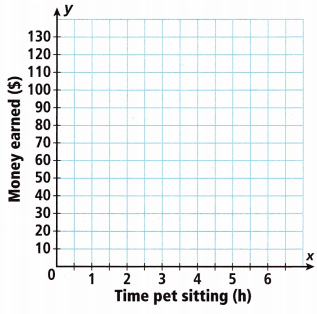
Answer:
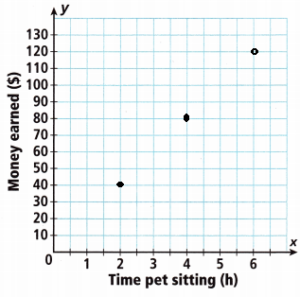
D. Use the graph to predict the unit rate, or amount that Tovah earns per hour. How can you use the table to check your prediction?
_______________________
_______________________
_______________________
Answer:
The unit rate is 1:20
Turn and Talk How can you find unknown values in a table of equivalent ratios?
Check Understanding
Question 1.
A snack shack sells trail mix packs and bottles of water during a softball game. The items are not sold individually. Instead, the snack shack only sells a “Snack Special” that contains 2 packs of trail mix and 3 bottles of water. Complete the table using equivalent ratios.

Answer:
The ratio of trail mix packs to bottles of water is 2:3
Let us complete the table by using the ratio.
Trail mix packs are multiples of 2 and bottles of water are multiples of 3.

Question 2.
A train travels at a constant speed for 420 miles. If it takes the train 7 hours to travel that distance, what is the unit rate at which the train travels?
Answer:
Given,
A train travels at a constant speed for 420 miles.
It takes the train 7 hours to travel that distance
To find what is the unit rate at which the train travels we have to divide 420 by 7.
420 ÷ 7 = 60
The unit rate at which the train travels is 60 miles.
On Your Own
Question 3.
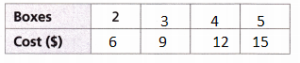
Open Ended A grocery store charges $6 for every 2 boxes of a certain cereal. Complete the table of equivalent ratios.

Answer:
Given,
A grocery store charges $6 for every 2 boxes of a certain cereal.
The ratio is 2:6 = 1:3
The equivalent ratios = 1 × 3:3 × 3 = 3:9
1 × 4: 3 × 4 = 4:12
1 × 5 : 3 × 5 = 5 : 15
Question 4.
A hotel advertises vacation packages on its website, and it charges the same amount per night. The table shows the total costs of stays for different numbers of nights.
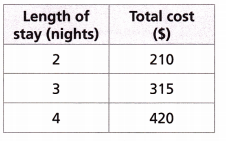
A. What is the unit rate per night? _____
Answer:
Given,
A hotel advertises vacation packages on its website, and it charges the same amount per night.
The above table shows the total costs of stays for different numbers of nights.
For 2 stays the cost is $210.
1 stay = x
x × 2 = 210
x = 210/2 = 105
Thus the cost of 1 stay is $105
The ratio is 1:105
Thus the unit rate per night is $105
B. What is the total cost for 5 nights? _________
Answer:
The ratio is 1:105
The total cost for 5 nights is x
1 × 5 : 105 × 5 = 5 : 525
Thus the total cost for 5 nights is $525.
Question 5.
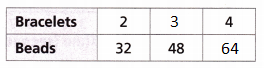
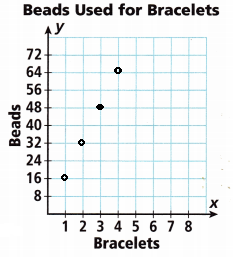
The table shows the number of beads a jeweler used to make bracelets. Each bracelet used the same number of beads.
A. Complete the table. Then graph the data.
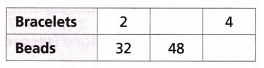
Answer:
The beads are multiple of 16.
The ratio bracelets to beads = 2:32 = 1:16
3:48 = 1:16
4:64 = 1:16
B. Write a ratio to show the number of beads necessary to make one bracelet.
______________
Answer:
C. How many beads would the jeweler need to make 10 bracelets?
______________
Answer:
The ratio of bracelets to beads is 1:16
The jeweler needs to make 10 bracelets.
1 × 10: 16 × 10 = 10:160
Thus the jeweler needs 160 beads to make 10 bracelets.
Question 6.
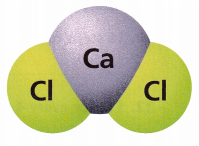
STEM Calcium chloride is a salt used in the production of cheese. It consists of calcium (Ca) and chlorine (Cl) atoms. A single calcium chloride molecule is shown in the illustration. Complete the table of equivalent ratios relating the number of calcium atoms to chlorine atoms in 1, 2, 3, 4, and 5 molecules of calcium chloride.

Answer:
Question 7.
Each week, Sachi has 3 soccer practices that each last 45 minutes. Write the unit rate in minutes per practice. Then find the total time she practices soccer each week.
Answer:
Each week, Sachi has 3 soccer practices that each last 45 minutes.
3 soccer practices = 45 minutes
1 soccer practice = x
x × 3 = 45
x = 45/3
x = 15
Thus the unit rate in minutes per practice is 15 minutes.
Lesson 5.2 More Practice/Homework
Represent Ratios and Rates with Tables and Graphs
Question 1.
The table shows the amount of money that Roberto earns mowing lawns.
A. How much does Roberto earn per lawn mowed? Show your reasoning using ratios.
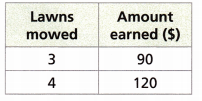
_________________
Answer:
Given that,
The table shows the amount of money that Roberto earns mowing lawns.
Roberto earn $90 for 3 lawns mowed = 90/3 = 30
Roberto earn $120 for 4 lawns mowed = 120/4 = 30
Therefore Roberto earns $30 per lawn mowed.
B. Reason When finding ratios, did it matter whether you used the values for 3 lawns mowed or the values for 4 lawns mowed? Explain.

Answer:
Yes because the income of Robert depends on the number of lawns mowed.
So, it is necessary to use values for 3 lawns mowed or the values for 4 lawns mowed.
For Problems 2-3, complete the table using equivalent ratios.
Question 2.
8 pairs of black shoes for every 3 pairs of red shoes
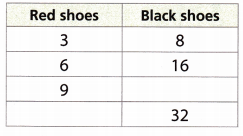
Answer:
Given,
8 pairs of black shoes for every 3 pairs of red shoes
The ratio is 3:8
Equivalent ratios are 3 × 2:8 × 2 = 6:16
3 × 3 : 8 × 3 = 9:24
3 × 4 : 8 × 4 = 12:32
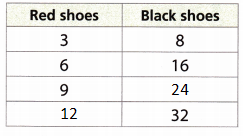
Question 3.
$25 for every 2-hour art class
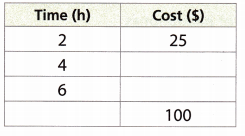
Answer:
Given,
$25 for every 2-hour art class
The ratio of time to cost is 2:25
The equivalent ratios are 2:25, 4:50, 6:75 and 8:100
Question 4.
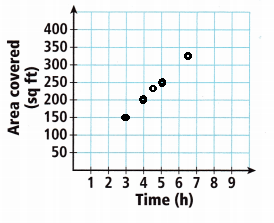
Math on the Spot Eric lays tile on a floor at a constant rate. He covers a 150-square-foot floor in 3 hours.
A. Complete the table to show the area Eric can cover in various amounts of time.

Answer:
Eric lays tile on a floor at a constant rate. He covers a 150-square-foot floor in 3 hours.
150 square ft = 3 hours
x = 1 hour
x × 3 = 150
x = 150/3
x = 50
He covers 50 square foot floor in 1 hour
With the help of this data, we can complete the table.
4 hours = 4 × 50 = 200 sq. ft
4.5 = 4.5 × 50 = 225 sq. ft
5 = 5 × 50 = 250 sq. ft
6.5 = 6.5 × 50 = 325 sq. ft

B. Graph the information from the table.
Answer:
For Problems 5-6, find the unit rate.
Question 5.
56 ounces for every 2 cans
_______________
Answer:
56 ounces for every 2 cans
2 cans = 56 ounces
1 can = x
x × 2 = 56
x = 56/2
x = 28
Thus 28 ounces for each can.
Question 6.
$5.15 per 5-pound bag
_______________
Answer:
$5.15 per 5-pound bag
5 pound = $5.15
1 pound = x
x × 5 = $5.15
x = 5.15/5
x = 1.03
Thus the cost of 1 pound bag is $1.03
Test Prep
Question 7.
Steel is a mixture of iron, carbon, and other elements. The table shows the number of parts of each element in two different-sized samples of steel.

A. What is the unit rate of parts iron to parts carbon?
_______________________
Answer:
Number of parts of iron in sample 1 = 90
Number of parts of carbon in sample 1 = 3
The ratio of parts iron to parts carbon = 90/3 = 30/1
Number of parts of iron in sample 2 = 45
Number of parts of carbon in sample 2 = 1.5
The ratio of parts iron to parts carbon = 45/1.5 = 30/1
So, the unit rate of parts iron to parts carbon is 30.
B. What is the unit rate of parts iron to parts all other elements, including carbon?
_______________________
Answer:
The unit rate of parts iron to parts all other elements including carbon is
90/3+7 = 90/10 = 9
Question 8.
The graph shows the costs of pairs of headphones. Which ratios are represented by a point on the graph? Select all that apply.
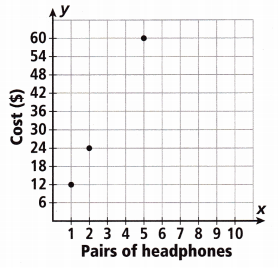
A. $2 for every 24 pairs of headphones
B. $5 for every 60 pairs of headphones
C. $6 per pair of headphones
D. $12 per pair of headphones
E. 2 pairs of headphones to $24
F. 5 pairs of headphones to $54
Answer:
D. $12 per pair of headphones
E. 2 pairs of headphones to $24
Explanation:
By using the graph given above we can find the ratios are represented by a point on the graph.
1 pair of headphones = $12
2 pairs of headphones = 2 × 12 = 24
Thus options D and E are the correct answers.
Spiral Review
Question 9.
Find the quotient.
12.462 ÷ 0.04
______________
Answer:
12.462 ÷ 0.04 = 311.55
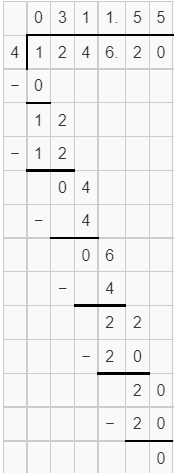
The quotient of 12.462 by 0.04 is 311.55
Question 10.
Ann spends $59.95 on a skateboard and $19.18 on a helmet, including tax. What is the total cost?
Answer:
Given,
Ann spends $59.95 on a skateboard and $19.18 on a helmet, including tax.
59.95 + 19.18 = 79.13
Thus the total cost is $79.13
Question 11.
The length of a path from a picnic area to the playground is \(\frac{3}{4}\) mile. The path has signs with arrows pointing to the playground every \(\frac{1}{8}\) mile. How many signs are placed along the path, assuming that there is a sign at the beginning of the path but not at the end?
Answer:
Given,
The length of a path from a picnic area to the playground is \(\frac{3}{4}\) mile.
The path has signs with arrows pointing to the playground every \(\frac{1}{8}\) mile.
We have to divide \(\frac{1}{8}\) by \(\frac{3}{4}\) to find how signs are placed along the path, assuming that there is a sign at the beginning of the path but not at the end.
\(\frac{3}{4}\) ÷ \(\frac{1}{8}\)
\(\frac{3}{4}\) × 8 = 3 × 2 = 6
Therefore 6 signs are placed along the path at the beginning of the path but not at the end.