Into Math Grade 6 Module 5 Answer Key Ratios and Rates

We included HMH Into Math Grade 6 Answer Key PDF Module 5 Ratios and Rates to make students experts in learning maths.

HMH Into Math Grade 6 Module 5 Answer Key Ratios and Rates

Music Producer

Music producers play key roles in all aspects of music recording. They may help choose songs for an album, coach singers and other musicians, manage recording sessions, and more. Music producers often work for record companies and may help to find new musical acts and sign them to contracts. One purpose of a contract is to specify the amount of money a musician receives when songs are streamed or downloaded.

STEM Task
Thomas Edison invented the phonograph with records shaped like cylinders in 1877. Soon after, Emile Berliner introduced the gramophone and the disc-shaped phonograph record. Early records were designed to spin 78 times Per minute- Later records spun either 45 or 33\(\frac{1}{3}\) times per minute. For each of these three speeds, find the number of full revolutions Jr a record completes in 3 minutes. Explain your reasoning.

Learning Mindset
Challenge-Seeking Defines Own Challenges

Finding the appropriate level of challenge can be tricky. On the one hand, a task that is familiar and easy can lead to boredom and carelessness. On the other hand, a task that is too difficult may cause you to feel frustrated and discouraged. Here are some suggestions for keeping an appropriate level of challenge in your work. Can you think of others?

• If you are bored or uninterested, try to determine why. Is it because the task is too easy or too difficult?
• If a task is too difficult, can you break it down into easier pieces that are more manageable?
• If a task is too easy, can you find a new and creative way to complete it? How many ways can you find to finish the task? Can you find ways to extend or expand upon the task?

Reflect

Question.
How do you know whether a task is an appropriate challenge for you? Did the STEM Task have the right level of challenge?

Question.
How could you modify the STEM Task to make it more challenging? Less challenging?

Use Paint Patterns

The cafeteria at Frost Middle School is being painted sky blue. The table shows the amounts of bright blue paint that must be mixed with different amounts of white paint to make sky-blue paint.

Use number patterns to complete the table and answer the questions.

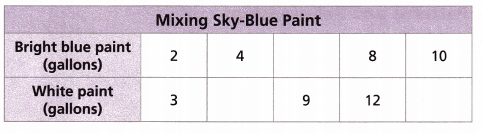
The painting crew needs 40 gallons of sky-blue paint for the cafeteria. What amounts of bright blue paint and white paint should they mix?
______ gallons of bright blue paint and ___ gallons of white paint.
Answer:

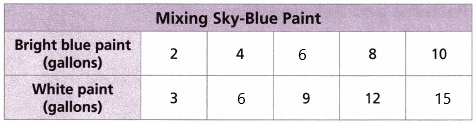
30 gallons of bright blue paint and 15 gallons of white paint.

Turn and Talk

• Describe the patterns you used to complete the table.
  Answer: The pattern we can use is an arithmetic sequence for both bright blue paint and white paint.
  – we need to add the number ‘2’ to the previous number to get the next number 2 +2 = 4; 4 +2 = 6; 6 + 2 = 8; 8 + 2 = 10.
  For white paint, we need to add 3 to the previous number to get the next number
  3 + 3 = 6; 6 + 3 = 9; 9 + 3 = 12; 12 + 3 = 15
• How did you use patterns in the table to find the amounts of bright blue paint and white paint needed for the cafeteria?
  Answer:
  Added all the gallons of bright blue and white paint needed for the cafeteria
  Let the bright blue be x.
  x = 2 + 4 + 6+ 8 + 10
  X = 30
  Let the white paint be Y.
  Y = 3 + 6 + 9 + 12 + 15
  Y = 45

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Multiply or Divide to Find Equivalent Fractions

Multiply or divide to find the equivalent fraction.

Question 1.

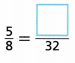
Answer:
Let the empty box be M.

Therefore, the value of the empty box is 20.

Question 2.

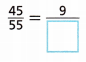
Answer:
Let the empty box be M.

therefore, the value of the empty box is 11.

Question 3.

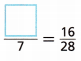
Answer:
Let the empty box be M.

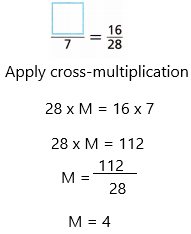
Therefore, the value of the empty box is 4.

Find two equivalent fractions, one by multiplying and one by dividing.

Question 4.
\(\frac{12}{16}\)
___________________
Answer:
Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value.
There is an infinity number of equivalent fractions to 12/16.
To find an equivalent fraction to 12/16, or to any other fraction, you just need to multiply (or divide, if the fraction is not yet reduced), both the numerator and the denominator of the given fraction by any non-zero natural number.
By dividing the original fraction by 4, we get:

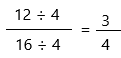
By multiplying the original fraction by 2, we get:

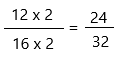
There are some more equivalent fractions to 12/16.
3/4, 6/8, 9/12, 12/16, 15/20, 18/24, 21/28, 24/32, 27/36, 30/40, 33/44 and so on…

Question 5.
\(\frac{8}{10}\)
___________________
Answer:
Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value.
There is an infinity number of equivalent fractions to 8/10.
To find an equivalent fraction to 8/10, or to any other fraction, you just need to multiply (or divide, if the fraction is not yet reduced), both the numerator and the denominator of the given fraction by any non-zero natural number.
By dividing the original fraction by 2, we get:

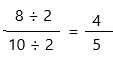
By multiplying the original fraction by 2, we get:

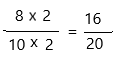
There are some more equivalent fractions to 8/10
4/5, 8/10, 12/15, 16/20, 20/25,  24/30, 28/35, 32/40, 36/45, 40/50, 44/55, 48/60, 52/65, 56/70, 60/75, 64/80, 68/85, 72/90, 76/95, 80/100 …

Question 6.
\(\frac{9}{15}\)
___________________
Answer:
There is an infinity number of equivalent fractions to 9/15.
To find an equivalent fraction to 9/15, or to any other fraction, you just need to multiply (or divide, if the fraction is not yet reduced), both the numerator and the denominator of the given fraction by any non-zero natural number.
By dividing the original fraction by 3, we get:

By multiplying the original fraction by 2, we get:

There are some more equivalent fractions to 9/15
3/5, 6/10, 9/15, 12/20, 15/25, 18/30, 21/35, 24/40, 27/45, 30/50, 33/55, 36/60, 39/65, 42/70, 45/75, 48/80, 51/85, 54/90, 57/95, 60/100 …

Analyze Patterns and Relationships

Complete each pattern.

Question 7.
10, 15, 20, ___, ___, ___, ____, ___
Answer:
This pattern comes under arithmetic sequence.
Arithmetic sequences are sequences of numbers with constant differences between consecutive terms in mathematics. Common differences between consecutive terms are called common differences.
The given pattern is 10, 15, 20,- – – – –
The next number is 25, 30, 35, 40, 45, 50, 55… is an arithmetic sequence because the difference between consecutive terms is 5.
Add the number ‘5’ to the previous number to get the next number.
10 + 5 = 15; 15 + 5 = 20; 20 + 5 = 25; 25 + 5 = 30; 30 + 5 = 35; 30 + 5 = 35; 35 + 5 = 40.
Hence, the sequence is 10, 15, 20, 25, 30, 35, 40, 45.

Question 8.
17, 22. 27, ___, ___, ___, ____, ____
Answer:
This pattern comes under arithmetic sequence.
Arithmetic sequences are sequences of numbers with constant differences between consecutive terms in mathematics. Common differences between consecutive terms are called common differences.
The given pattern is 17, 22, 27,- – – – –
The next number is 32, 37, 42, 47, and 52 is an arithmetic sequence because the difference between consecutive terms is 5.
Add the number ‘5’ to the previous number to get the next number.
17 + 5 = 22; 22 + 5 = 27; 27 + 5 = 32; 32 + 5 = 37; 37 + 5 = 42; 42 + 5 = 47; 47 + 5 = 52.
Hence, the sequence is 17, 22, 27, 32, 37, 42, 47, 52.

Question 9.
How are the patterns related?
___________________
___________________
___________________
Answer:
A number pattern is the most common type of pattern in mathematics where a list of numbers follows a certain sequence based on a rule. The different types of number patterns are algebraic or arithmetic patterns, geometric patterns, and the Fibonacci pattern.
Arithmetic pattern: Arithmetic Pattern, also known as the algebraic pattern, is a sequence of numbers based on addition or subtraction to form a sequence of numbers that are related to each other. If two or more numbers in the sequence are given, we can use addition or subtraction to find the arithmetic pattern. We can also determine the missing number in a given sequence by using addition or subtraction.
Geometric pattern: Geometric pattern is a sequence of numbers that are based on multiplication and division. If two or more numbers in the sequence are provided, we can easily find the unknown numbers in the pattern using multiplication and division operations.
Fibonacci pattern: The Fibonacci Pattern is a sequence of numbers in which each number in the sequence is obtained by adding the two previous numbers together. The sequence starts with 0 and 1. Observe this Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, and so on. Here, we can see the pattern that is followed is: 0 + 1 = 1,  1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5, 3 + 5 = 8.

Division Involving Decimals

Find the quotient.

Question 10.
11.6 ÷ 4 _____
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.

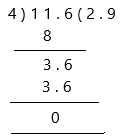
Therefore, the quotient is 2.9 and the remainder is 0.

Question 11.
48 ÷ 0.6 _____
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.
-Change the divisor 0.6 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
480 ÷ 6 = 80.000
and therefore:
48 ÷ 0.6 = 80.000
Both are calculated to 3 decimal places.

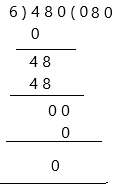
Therefore, the quotient is 80 and the remainder is 0.

Question 12.
1.18 ÷ 0.2 _____
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.
Change the divisor 0.2 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
11.8 ÷ 2 = 5.900
and therefore:
1.18 ÷ 0.2 = 5.900
Both are calculated to 3 decimal places.

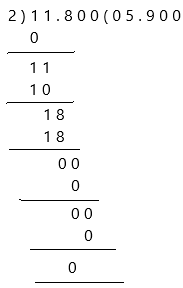
Therefore, the quotient is 5.900 and the remainder is 0.

Question 13.
4.96 ÷ 1.6 ______
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.
Change the divisor 1.6 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
49.6 ÷ 16 = 3.100
and therefore:
4.96 ÷ 1.6 = 3.100
Both are calculated to 3 decimal places.

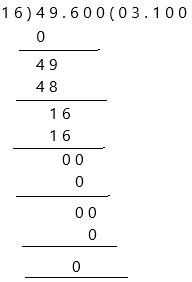
Therefore, the quotient is 3.1 and the remainder is 0.

Question 14.
5.4 ÷ 3.6 ____
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.
– Change the divisor 3.6 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
54 ÷ 36 = 1.500
and therefore:
5.4 ÷ 3.6 = 1.500
Both are calculated to 3 decimal places.

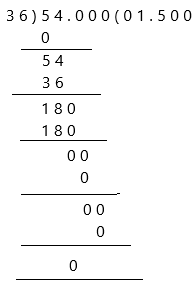
Therefore, the quotient is 1.5 and the remainder is 0.

Question 15.
7.67 ÷ 1.3 ______
Answer:
a decimal number is a number that has the whole number part a decimal part separated by a dot called a decimal point. There are two different possibilities for dividing a decimal number. They are
– Dividing a decimal number by a whole number
– Dividing a decimal number by another decimal number
In the division process, if the remainder becomes 0 and the quotient has some decimal values,  then it is called terminating decimals. In another case, the remainder is not equal to 0 and the quotient has some repeating values in the decimal places, then it is called recurring decimals.
– Change the divisor 1.3 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
76.7 ÷ 13 = 5.900
and therefore:
7.67 ÷ 1.3 = 5.900
Both are calculated to 3 decimal places.

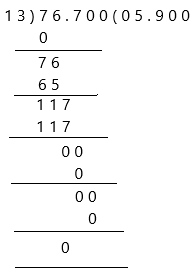
Therefore, the quotient is 5.900 and the remainder is 0.