We included HMH Into Math Grade 6 Answer Key PDF Module 4 Review to make students experts in learning maths.
HMH Into Math Grade 6 Module 4 Review Answer Key
Vocabulary
sum
difference
divisor
dividend
equivalent
remainder
Choose the correct term from the Vocabulary box.
Question 1.
In the problem 3.8 ÷ 0.7, the number 3.8 is the _____ and the number 0.7 is the ____
Answer:
3.8 is the dividend
A dividend is a whole number or the number of things that need to be divided into certain equal parts.
0.7 is the divisor.
The number by which the dividend is to be divided is called the divisor.
Question 2.
The solution to an addition problem is called the _____
Answer: sum
The addition is the term used to describe adding two or more numbers together. The addition is denoted using the plus sign ‘+‘ such as the addition of 3 and 3 can be written as 3 + 3. Also, the plus sign (+) can be used as many times as required, such as 3 + 4
The parts of addition can be shown below:
For example, take 5 + 4 = 9
5 and 4 are the addends
‘+’ is the operating symbol
‘=’ equality symbol
9 is the sum/total
Question 3.
The solution to a subtraction problem is called the ____
Answer: difference.
The result of subtraction is called the difference.
When a number is subtracted from another number, then the result produced will be another value called the difference of the two numbers.
For example,
10 – 4 = 6
Here, 10 is minuend, 4 is subtrahend and 6 is the difference.
Question 4.
Two division expressions that have the same value are _____
Answer: equivalent
Equivalent expressions are expressions that work the same even though they look different. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value for the variable.
Concepts and Skills
Question 5.
The distance from Jose’s home to school is 1.85 miles. The school is 2.34 miles from the local library, which is 1.9 miles from Jose’s home. If Jose goes from his home to school, from school to the library, and then home, how far does he travel?
____ miles
Answer:
The miles from Jose’s home to school=1.85
The miles from the local library to school = 2.34
The miles from Jose’s home to the library = 1.9
The miles he travels = X
X= 1.85 + 2.34 + 1.9
X = 6.09.
Therefore, finally, he travels 6.09 miles.
Question 6.
An aeroplane flew a total of 6,240 miles. Its speed was 520 miles per hour. How many hours did the plane fly?
___ hours
Answer:
The total miles an aeroplane flew = 6,240
The number of miles an aeroplane speed per hour = 520
The number of hours the plane flew = X
for 1 hour, an aeroplane will fly 520 miles.
for X hours, an aeroplane will fly 6,240 miles.
Apply cross-multiplication.
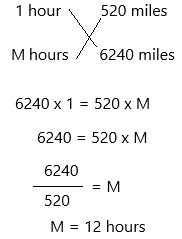
Therefore, an aeroplane can fly for 12 hours.
Question 7.
Use Tools Telegraphs were used to send messages before the telephone was invented. A telegraph operator could interpret about 40 words sent in Morse code per minute. Approximately how many words sent in Morse code could the operator interpret in 12.5 seconds? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
we all know that 1 minute is equal to 60 seconds.
For 60 seconds, a telegraph operator could interpret 40 words in Morse code.
For 12.5 seconds, how many words he can interpret. Assume it be W.
We can apply cross-multiplication.
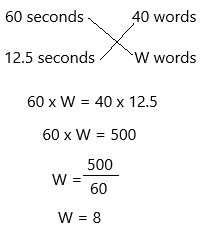
Therefore, a telegraph operator can interpret 8 words in 12.5 seconds.
Question 8.
Which has a quotient of 0.6?
A 0.204 ÷ 0.034
B. 0.204 ÷ 0.34
C. 2.04 ÷ 0.034
D. 2.04 ÷ 0.34
Answer: Option B is correct.
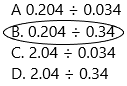
In this problem, we need to go for the option verification process.
Now verify each option and whatever option is getting 0.6 is the quotient that option will be the correct.
0.204 ÷ 0.34 = 0.6
Multiplying the numerator and denominator by 100

Question 9.
The ocean rises and falls each day due to tides. The Bay of Fundy in Canada has some of the highest tides in the world. Its tidewater rises about 53.478 feet and falls the same amount afterwards, twice a day.
A. Write an expression that can be used to find the total number of feet the tide rises and falls each day.
________________________
Answer:
We need to write an algebraic expression;
The feet that rise a day = 53.478/2
The feet that rise a day = 26.739
The feet that fall the same amount afterwards=26.739
The expression for the total number of feet the tide rises and falls each day = X
X = 26.739 + 26.739
X = 53.478
Therefore, the total number of feet the tide rises and falls each day is 53.478.
B. Write an expression that can be used to find the total number of feet the tide rises and falls over a one-week period.
________________________
Answer:
one week is equal to 7 days.
The expression to find the total number of feet the tide rises and falls over a one-week period = X
X = 7 ( 26.739 + 26.739 )
X = 7 ( 53.478 )
X = 374.346
C. How many total feet does the tide rise and fall over a one-week period?
________________________
Answer:
We need to write an algebraic expression;
The feet that rise a day = 53.478/2
The feet that rise a day = 26.739
The feet that fall the same amount afterwards=26.739
The expression for the total number of feet the tide rises and falls each day = X
X = 26.739 + 26.739
X = 53.478
Therefore, the total number of feet the tide rises and falls each day is 53.478.
One week is equal to 7 days.
the total feet the tide rises and falls over a one-week period = Y
Y = 7 (53.478)
Y = 374.346
Therefore, at 374.346 feet the tide rises and falls over a one-week period.
Question 10.
A 0.5-pound bunch of bananas costs $0.22 and 1 pound of oranges costs $2.39. If a person has $20, which expression could be used to determine how much change the person would get after purchasing the 0.5-pound bunch of bananas a 3.25 pounds of oranges?
A. 20 – 0.22 + (2.39 × 3.25)
B. 0.22 + (2.39 x 3.25) – 20
C. 20 – [0.22 + (3.25 × 2.39)]
D. 0.22 + (0.5 × 3.25) – 20
Answer: Option C is correct.
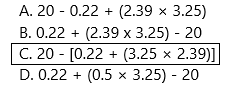
The total amount a person has = $20
The cost of a 0.5-pound bunch of banans=$0.22
The cost of 1-pound oranges = $2.39
If a person purchases 0.5-pound of bananas and 3.25 pounds of oranges be X.
The expression would be:
X = 20 – [ 0.22 + (3.25 × 2.39) ]
X = 20 – [ 0.22 + 7.7675 ]
X = 20 – [ 7.9875 ]
X = 12.0125
Question 11.
A bag of equally-sized rhinestones weighs 16 ounces. Each rhinestone weighs 0.016 ounces. If you have 2 bags of rhinestones, how many rhinestones do you have?
________________________
Answer:
1 pound = 16 ounces
The weight of each rhinestone is 0.016
The size of a bag of rhinestones is 16 ounces.
In each bag, the number of rhinestones = 0.016/16 = 0.001
If we have 2 bags of rhinestones then the weights of the bag = 16 x 2 = 32 ounces.
The number of rhinestones = 0.016/32 = 0.0005
Question 12.
What is the value of the expression?
7.09 – (1.36 × 4.125) + (3.28 ÷ 0.04)
A. 8.85
B. 9.68
C. 83.39
D. 83.48
Answer: Option D is correct.

The given expression:
7.09 – (1.36 × 4.125) + (3.28 ÷ 0.04)
= 7.09 – (1.36 × 4.125) + (3.28/0.04)
Remove parentheses: (a) = a
= 7.09 – 1.36 x 4.125 + 3.28/0.04
Multiplying the numbers:
= 7.09 – 5.61 + 3.28/0.04
Now subtract the numbers: (7.09 – 5.61 = 1.48)
= 3.28/0.04 + 1.48
Divide the numbers: 3.28/0.04 = 82
= 82 + 1.48
Now add the numbers:
= 83.48
Therefore the value of the above-given expression is 83.48
Question 13.
Remy is saving money to buy a new video game console. The console costs $199.95. Remy makes $40.50 each week babysitting. How many total weeks will he need to babysit to save up enough money for the video game console? Explain your reasoning.
Answer:
The cost of a new video game console is $199.95
The amount Remy makes each week babysitting = $40.50
The total weeks will he need to babysit to save up enough money for the video game console = X
For each week, he makes $40.50
For X weeks, he makes $199.95
Apply cross-multiplication

Therefore, he takes 5 weeks to make enough money.