We included HMH Into Math Grade 6 Answer Key PDF Module 3 Lesson 1 Understand Fraction Division to make students experts in learning maths.
HMH Into Math Grade 6 Module 3 Lesson 1 Answer Key Understand Fraction Division
I Can divide fractions with like denominators with and without models.
Spark Your Learning
Jayson is making sushi rolls. He has \(\frac{5}{6}\) cup of rice and will use \(\frac{2}{6}\) cup for each sushi roll. How many whole sushi rolls can he make?


Answer:
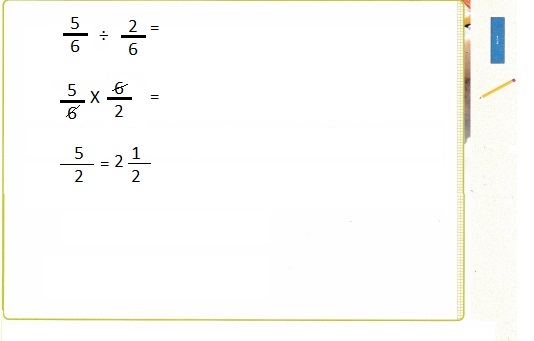
2 whole sushi rolls,
Explanation:
Given Jayson is making sushi rolls. He has 5/6 cup of
rice and will use 2/6 cup for each sushi roll.
2 whole sushi rolls can he make.
Turn and Talk How many sushi rolls can Jayson make if he uses up all the rice? Explain.
Answer:
2 1/2 sushi rolls,
Explanation:
Given Jayson is making sushi rolls. He has
5/6 cup of rice and will use
\(\frac{2}{6}\) cup for each sushi roll,
Number of sushi rolls can Jayson make if he uses
up all the rice is \(\frac{5}{6}\) ÷ \(\frac{2}{6}\) =
\(\frac{5}{6}\) X \(\frac{6}{2}\) =
\(\frac{5 X 6}{6 X 2}\) = \(\frac{5}{2}\)
as numerator is greater than denominator we write in
mixed fraction as 2\(\frac{1}{2}\).
Therefore sushi rolls can Jayson make if he uses up all the rice are
2\(\frac{1}{2}\).
Build Understanding
1. Malik is making eggrolls to share with Jayson. Malik has \(\frac{4}{5}\) pound of chicken and will use the amount shown per batch. How many batches of eggrolls can Malik make?

A. Write an expression to show how you would divide a fraction by a fraction to solve this problem.
_____ ÷ _____
B. Explain how you can use a model to find how many groups of \(\frac{2}{5}\) are in \(\frac{4}{5}\). Then make a model.

C. How many groups of \(\frac{2}{5}\) are there in \(\frac{4}{5}\) ? How many batches of eggrolls can Malik make?
Answer:
A. Expression:
4/5 ÷ 2/5,
B. 2 groups, Area Model,
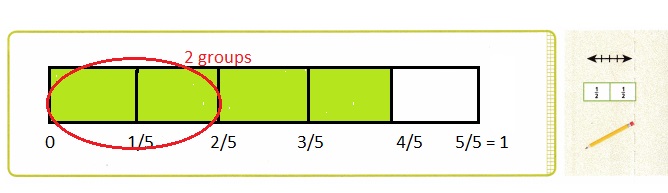
C. 2 groups and 2 batches of eggrolls can Malik make,
Explanation:
Given Malik is making eggrolls to share with Jayson.
Malik has \(\frac{4}{5}\) pound of chicken and
will use the amount \(\frac{2}{5}\) pound per batch
A. An expression to show how I would divide a fraction
by a fraction to solve this problem is
\(\frac{4}{5}\) ÷ \(\frac{2}{5}\).
B. Drawn a area model with \(\frac{4}{5}\)
and in that there are 2 groups of \(\frac{2}{5}\).
Then made a model as shown above circled 2 groups of
\(\frac{2}{5}\).
C. Number of groups of \(\frac{2}{5}\) are
there in \(\frac{4}{5}\) are
\(\frac{4}{5}\) ÷ \(\frac{2}{5}\) =
\(\frac{4}{5}\) X \(\frac{5}{2}\) =
\(\frac{4 X 5}{5 X 2}\) = 2, 2 batches of eggrolls
can Malik make.
2. Suppose Malik had \(\frac{3}{4}\) pound of chicken and uses \(\frac{3}{8}\) pound to make one batch of eggrolls. How many batches of eggrolls could he make?
A. Draw the fraction strip you could use to begin to find the solution.
B. Will the fraction strip you drew in Part A help you to make groups of \(\frac{3}{8}\)? If not, what other fraction strip could help? Explain why.
________________________
C. Draw the fraction strip you chose in Part B in the answer box in Part A. How many groups of \(\frac{3}{8}\) are in \(\frac{3}{4}\)? Explain.
D. How many batches of eggrolls can Malik make?
________________________
Answer:
A.

B. Yes, the fraction strip I drew in Part A will help me
to make groups of 3/8,
C.
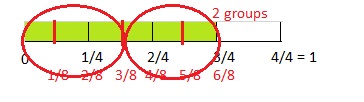
2 groups,
D. 2 batches,
Explanation:
Given Malik had \(\frac{3}{4}\) pound of
chicken and uses \(\frac{3}{8}\) pound to
make one batch of eggrolls.
A. Drawn the fraction strip I could use to begin
to find the solution as \(\frac{3}{4}\),
B. The fraction strip I drew in Part A will help me
to make groups of \(\frac{3}{8}\),
C. Drawn the fraction strip that I chose in
Part B in the answer box in Part A.
Two groups of \(\frac{3}{8}\)
are in \(\frac{3}{4}\) as shown above
circled with red color.
D. Number of batches of eggrolls could he make are
\(\frac{3}{4}\) ÷ \(\frac{3}{8}\) =
\(\frac{3}{4}\) X \(\frac{8}{3}\) =
\(\frac{3 X 8}{4 X 2}\) = 2, 2 batches of eggrolls
can Malik make.
3. Suyin is making a dog house. She needs to cut a board that is \(\frac{5}{9}\) yard long into smaller pieces. How many pieces can she cut if each piece needs to be \(\frac{2}{9}\) yard long?
A. Complete the following to express the problem in words. Suyin needs to find how many groups of ____ are in ____.

B. What division expression can you use to answer this question?
_________________
C. Complete the bar model to show the division problem in Part B.
![]()
D. Write an explanation of how the bar model represents the quotient in Part B.

E. What is the number of pieces of board, each \(\frac{2}{9}\) yard long, that Suyin an cut? Did Suyln use up all the wood? If not, how long Is the leftover piece of board?
Answer:
A. Suyin needs to find how many groups of
\(\frac{2}{9}\) are in \(\frac{5}{9}\),
B. Division expression:
\(\frac{5}{9}\) ÷ \(\frac{2}{9}\),
C. 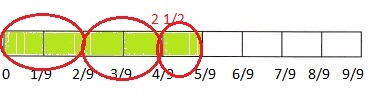
D. 
E. The number of pieces of board each
\(\frac{2}{9}\) yard long that Suyin can cut is 2,
No Suyin has not used up all the wood
\(\frac{1}{2}\) is the leftover piece of board,
Explanation:
Given Suyin is making a dog house. She needs to cut a
board that is \(\frac{5}{9}\) yard long into smaller pieces.
If each piece needs to be \(\frac{2}{9}\) yard long
A. Completed the following to express the problem in words as
Suyin needs to find how many groups of
\(\frac{2}{9}\) are in \(\frac{5}{9}\),
B. Division expression I can use to answer this question is
Division expression:
\(\frac{5}{9}\) ÷ \(\frac{2}{9}\).
C. Completed the bar model to show the division
problem in Part B above.
D. Wrote an explanation of how the bar model
represents the quotient in Part B.
E. The number of pieces of board, each
\(\frac{2}{9}\) yard long, that Suyin can cut is 2,
No Suyin has not used up all the wood
\(\frac{1}{2}\) is the leftover piece of board.
Turn and Talk What fraction of another piece an Suyin make with what is left over?
Answer:
\(\frac{1}{2}\) fraction of another piece
Suyin can make with the leftover piece,
Explanation:
Given \(\frac{5}{9}\) ÷ \(\frac{2}{9}\) solving
\(\frac{5}{9}\) X \(\frac{9}{2}\) =
\(\frac{5 X 9}{9 X 2}\) = \(\frac{5}{2}\)
as numerator is greater than denominator we write in
mixed fraction as 2\(\frac{1}{2}\) therefore
\(\frac{1}{2}\) fraction of another piece
Suyin can make with the leftover piece.
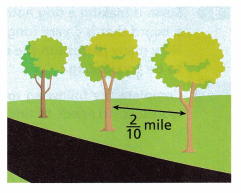
4. The diagram shows part of a road that is \(\frac{9}{10}\) mile long. Consider the expression \(\frac{9}{10}\) ÷ \(\frac{2}{10}\).
A. Write a problem that can be modeled with the given expression and that uses the information in the diagram.
B. Show or describe how to find the quotient.

C. Recall that the dividend is the number to be divided in a division problem. The divisor is the number you are dividing by. In your problem, what do the dividend and divisor represent?
_________________________
_________________________
D. How does the answer to the question in Part A compare to the quotient in Part B? Explain.
_________________________
Answer:
A. “A road is \(\frac{9}{10}\) mile long there are trees
each at a distance of \(\frac{2}{10}\) mile long,
how many trees are along the road side”,
B. 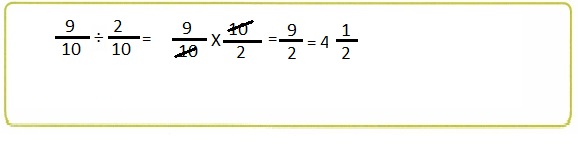
C. The dividend is \(\frac{9}{10}\) and
divisor is \(\frac{2}{10}\),
D. Part A question results are shown in part B,
Explanation:
Given the diagram shows part of a road that is
\(\frac{9}{10}\) mile long.
Considering the expression \(\frac{9}{10}\) ÷ \(\frac{2}{10}\)
A. Wrote a problem that can be modeled with the given
expression and that uses the information in the diagram as
“A road is \(\frac{9}{10}\) mile long there are trees
each at a distance of \(\frac{2}{10}\) mile long,
how many trees are along the road side”.
B. Described how to find the quotient as 4\(\frac{1}{2}\) above,
C. Recalled that the dividend is the number to be divided
in a division problem. The divisor is the number
we are dividing by. In my problem, the dividend is
\(\frac{9}{10}\) and divisor is \(\frac{2}{10}\).
D. The answer to the question in Part A compared to the
quotient in Part B is the question of Part A is how many trees are
along the road side and the result is shown in Part B.
Check Understanding
Question 1.
Hana is organizing a \(\frac{3}{4}\)-mile fun run. There will be a water station every \(\frac{1}{4}\) mile after the start.
A. How many groups of \(\frac{1}{4}\) are in \(\frac{3}{4}\)? ___________
Answer:
3 groups,
Explanation:
Given Hana is organizing a \(\frac{3}{4}\)-mile fun run.
There will be a water station every \(\frac{1}{4}\) mile after the start,
number of groups of \(\frac{1}{4}\) are in \(\frac{3}{4}\) are
\(\frac{3}{4}\) ÷ \(\frac{1}{4}\) solving
\(\frac{3}{4}\) X \(\frac{4}{1}\) = 3 groups.
B. How many water stations will there be? ___________________
Answer:
3 water stations,
Explanation:
Given Hana is organizing a \(\frac{3}{4}\)-mile fun run.
There will be a water station every \(\frac{1}{4}\) mile after the start,
number of water stations are \(\frac{3}{4}\) ÷ \(\frac{1}{4}\),
solving \(\frac{3}{4}\) X \(\frac{4}{1}\) = 3 water stations.
Question 2.
Janice is cutting ribbon to decorate a present. She has \(\frac{7}{8}\) foot of ribbon. She needs to make pieces that are \(\frac{3}{8}\) foot each. How many \(\frac{3}{8}\)-foot pieces will she get from the \(\frac{7}{8}\)-foot ribbon? ___________
Answer:
Janice will get 2\(\frac{1}{3}\) pieces of
\(\frac{3}{8}\)-foot pieces will she get from the
\(\frac{7}{8}\)-foot ribbon,
Explanation:
Given Janice is cutting ribbon to decorate a present.
She has \(\frac{7}{8}\) foot of ribbon.
She needs to make pieces that are \(\frac{3}{8}\) foot each.
Number of \(\frac{3}{8}\)-foot pieces will she
get from the \(\frac{7}{8}\)-foot ribbon are
\(\frac{7}{8}\) ÷ \(\frac{3}{8}\) solving
\(\frac{7}{8}\) X \(\frac{8}{3}\) =
\(\frac{7 X 8}{8 X 3}\) = \(\frac{7}{3}\)
as numerator is greater than denominator we write in
mixed fraction as 2\(\frac{1}{3}\).
On Your Own
Question 3.
Jasmine has \(\frac{4}{5}\) pound of fertilizer. She wants to store the fertilizer in
separate containers, each with \(\frac{1}{5}\) pound of fertilizer. How many containers
will she need? ___________
Answer:
Jasmine needs 4 containers,
Explanation:
Given Jasmine has \(\frac{4}{5}\) pound of fertilizer.
She wants to store the fertilizer in separate containers,
each with \(\frac{1}{5}\) pound of fertilizer.
Number of containers will she need are
\(\frac{4}{5}\) ÷ \(\frac{1}{5}\) solving
\(\frac{4}{5}\) X \(\frac{5}{1}\) =
\(\frac{4 X 5}{5 X 1}\) = 4.
Question 4.
Reason A city places street lights at equal intervals along a city street beginning \(\frac{3}{8}\) mile from one end of the street. If the street is \(\frac{7}{8}\) mile long, how many street lights will the city use? Explain.

Answer:
2 street lights,
Explanation:
Given a city places street lights at equal intervals along a
city street beginning \(\frac{3}{8}\) mile from
one end of the street. If the street is \(\frac{7}{8}\) mile long,
Number of street lights will the city use is
\(\frac{7}{8}\) ÷ \(\frac{3}{8}\) solving
\(\frac{7}{8}\) X \(\frac{8}{3}\) =
\(\frac{7 X 8}{8 X 3}\) = \(\frac{7}{3}\)
as numerator is greater than denominator we write in
mixed fraction as 2\(\frac{1}{3}\). Therefore
2 street lights will the city use.
Question 5.
Eric has \(\frac{9}{16}\) pound of bird feed left. If he feeds his bird \(\frac{1}{8}\) pound each day, how many days can he feed the bird before he needs to buy more food?
Answer:
4\(\frac{1}{2}\) days can he feed the bird
before he needs to buy more food,
Explaantion:
Given Eric has \(\frac{9}{16}\) pound of bird feed left.
If he feeds his bird \(\frac{1}{8}\) pound each day,
Number of days can he feed the bird before he
needs to buy more food are
\(\frac{9}{16}\) ÷ \(\frac{1}{8}\) solving
\(\frac{9}{16}\) X \(\frac{8}{1}\) =
\(\frac{9 X 8}{16 X 1}\) = \(\frac{9}{2}\)
as numerator is greater than denominator we write in
mixed fraction as 4\(\frac{1}{2}\), Therefore
4\(\frac{1}{2}\) days can he feed the bird
before he needs to buy more food.
Question 6.
Daryl has \(\frac{2}{8}\) of a bag of dog food. His dog eats \(\frac{4}{9}\) of a bag per week.
A. How many weeks will the dog food last? __________
Answer:
Number of weeks will the dog food last is
\(\frac{9}{16}\),
Explanation:
Given Daryl has \(\frac{2}{8}\) of a bag of dog food.
His dog eats \(\frac{4}{9}\) of a bag per week.
Number of weeks will the dog food last is
\(\frac{2}{8}\) ÷ \(\frac{4}{9}\) solving
\(\frac{2}{8}\) X \(\frac{9}{4}\) =
\(\frac{2 X 9}{8 X 4}\) = \(\frac{9}{16}\) weeks.
B. What fraction strip could you use to solve this problem? Explain why.
________________________
________________________
Answer:
Area model,
Explanation:
By using the area model because it shows
a rectangular diagram for division problems,
in which the factors or the quotient and divisor
define the length and width of the rectangle.
Question 7.
How long will it take Sarah to paint \(\frac{11}{12}\) of a fence if she paints \(\frac{2}{12}\) of the fence each day?
___________________
Answer:
5\(\frac{1}{2}\) days it will take,
Explanation:
Given it will take Sarah to paint \(\frac{11}{12}\) of
a fence if she paints \(\frac{2}{12}\) of the fence each day
it will take \(\frac{11}{12}\) ÷ \(\frac{2}{12}\) solving
\(\frac{11}{12}\) X \(\frac{12}{2}\) =
\(\frac{11 X 12}{12 X 2}\) = \(\frac{11}{2}\)
as numerator is greater than denominator we write in
mixed fraction as 5\(\frac{1}{2}\), Therefore
it will take 5\(\frac{1}{2}\) days to paint the fence.
Question 8.
How many \(\frac{1}{3}\)-cup servings are there in \(\frac{10}{3}\) cups of dried beans?
___________________
Answer:
There are 10 servings of \(\frac{1}{3}\)-cup in
Explanation:
Asking to find number of \(\frac{1}{3}\)-cup
servings are there in \(\frac{10}{3}\) cups of dried beans,
So it is \(\frac{10}{3}\) ÷ \(\frac{1}{3}\),
\(\frac{10}{3}\) X \(\frac{3}{1}\) =
\(\frac{10 X 3}{3 X 1}\) = 10 servings.
Question 9.
Tressa’s home is \(\frac{4}{5}\) mile from school. Anton’s home is \(\frac{3}{5}\) mile from school. How many times the distance from Anton’s home to school is the distance from Tressa’s home to school?
Answer:
1\(\frac{1}{3}\) times the distance from Anton’s home to
school is the distance from Tressa’s home to school,
Explanation:
Given Tressa’s home is \(\frac{4}{5}\) mile from school.
Anton’s home is \(\frac{3}{5}\) mile from school.
So number of times the distance from Anton’s home to school is
the distance from Tressa’s home to school is
\(\frac{4}{5}\) ÷ \(\frac{3}{5}\),
\(\frac{4}{5}\) X \(\frac{5}{3}\) =
\(\frac{4 X 5}{5 X 3}\) = \(\frac{4}{3}\)
as numerator is greater than denominator we write in
mixed fraction as 1\(\frac{1}{3}\) times.
Question 10.
Model with Mathematics Tom is pouring \(\frac{3}{32}\)-gallon servings from a bottle that contains \(\frac{15}{32}\) gallon of tomato juice. Write and evaluate a division expression to find the number of servings in the bottle.
Answer:
Division expression : \(\frac{15}{32}\) ÷ \(\frac{3}{32}\),
5 number of servings in the bottel,
Explanation:
Given Tom is pouring \(\frac{3}{32}\)-gallon servings
from a bottle that contains \(\frac{15}{32}\) gallon of
tomato juice.The division expression to find the
number of servings in the bottle is
\(\frac{15}{32}\) ÷ \(\frac{3}{32}\),
\(\frac{15}{32}\) X \(\frac{32}{3}\) =
\(\frac{15 X 32}{32 X 3}\) = 5 servings.
Question 11.
Model with Mathematics It takes \(\frac{1}{3}\) pint of paint to cover a birdhouse. There are 12\(\frac{1}{3}\) pints of paint in a can. Write and evaluate a division expression to find the number of birdhouses that can be painted.
Answer:
Division expression:
12\(\frac{1}{3}\) ÷ \(\frac{1}{3}\),
Number of birdhouses that can be painted are 37,
Explanation:
Given it takes \(\frac{1}{3}\) pint of paint to
cover a birdhouse. There are 12\(\frac{1}{3}\) pints of
paint in a can. Division expression to find the number of
birdhouses that can be painted is
12\(\frac{1}{3}\) ÷ \(\frac{1}{3}\) =
\(\frac{12 X 3 + 1}{3}\) X \(\frac{3}{1}\) =
\(\frac{37}{3}\) X 3 = 37.
Question 12.
Juan has \(\frac{5}{8}\) pound of beef. He wants to make burgers using the meat. If the meat in each burger weighs \(\frac{1}{8}\) pound, how many burgers can he make?
_________________
Answer:
5 burgers he can make,
Explanation:
Given Juan has \(\frac{5}{8}\) pound of beef.
He wants to make burgers using the meat. If the meat in
each burger weighs \(\frac{1}{8}\) pound,
Number of many burgers can he make are
\(\frac{5}{8}\) ÷ \(\frac{1}{8}\) =
\(\frac{5 X 1}{8}\) X 8 = 5.
Question 13.
Felice lives \(\frac{9}{10}\) mile from a park. She needs to stop several times while walking her new puppy to the park, including her final stop when she reaches the park. How many times will she stop when walking to the park?

Answer:
3 times Felice should stopwhen walking to park,
Explanation:
Given Felice lives \(\frac{9}{10}\) mile from a park.
She needs to stop several times while walking her new puppy
to the park, including her final stop when she reaches the park.
Number of times will she stop when walking to the park are
\(\frac{9}{10}\) ÷ \(\frac{3}{10}\) =
\(\frac{9}{10}\) X \(\frac{10}{3}\) =
\(\frac{9 X 10}{10 X 3}\) = 3 times.
Question 14.
Critique Reasoning Darius says that \(\frac{1}{3}\) ÷ \(\frac{2}{3}\) is 2, because you can’t make groups of \(\frac{2}{3}\) from \(\frac{1}{3}\). so you need to make groups of \(\frac{1}{3}\) from \(\frac{2}{3}\). Darius’ answer is not correct. What mistake did he make? What is the correct answer?
Answer:
\(\frac{1}{2}\) is the correct answer,
Explanation:
Given Darius says that \(\frac{1}{3}\) ÷ \(\frac{2}{3}\) is 2,
because you can’t make groups of \(\frac{2}{3}\)
from \(\frac{1}{3}\). so I need to make groups of
\(\frac{1}{3}\) from \(\frac{2}{3}\).
Darius’ answer is not correct. He made mistake in calculations
\(\frac{1}{3}\) ÷ \(\frac{2}{3}\) =
\(\frac{1}{3}\) X \(\frac{3}{2}\) =
\(\frac{1 X 3}{3 X 2}\) = \(\frac{1}{2}\).
So the correct answer is \(\frac{1}{2}\) not 2.
Question 15.
Write and solve a real-world problem that can be modeled by the diagram shown and the division expression \(\frac{3}{6}\) ÷ \(\frac{4}{6}\).
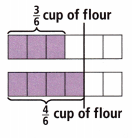
Answer:
Explanation:
World problem:”Nancy has \(\frac{3}{6}\) flour,
She needs \(\frac{4}{6}\) flour to make cake how much
part can she prepare the cake”,
Nancy can prepare \(\frac{3}{4}\) portion,
Explanation:
Asking to write and solve a real-world problem that
can be modeled by the diagram shown and the division
expression \(\frac{3}{6}\) ÷ \(\frac{4}{6}\) is
World problem: “Nancy has \(\frac{3}{6}\) flour,
She needs \(\frac{4}{6}\) flour to make cake how much
part can she prepare the cake”, solving
\(\frac{3}{6}\) ÷ \(\frac{4}{6}\) =
\(\frac{3}{6}\) X \(\frac{6}{4}\) =
\(\frac{3 X 6}{6 X 4}\) = \(\frac{3}{4}\) part.
I’m in a Learning Mindset!
Is using a model to divide fractions an effective strategy? Why or why not?
___________________________
___________________________
Answer:
Yes it is effective strategy,
Explanation:
As division is an essential foundation for fractions.
We can divide objects into equal groups,
We can begin to grasp dividing a whole into equal parts.
Dividing fractions using models makes this tricky topic
easier to visualize and find results.
Lesson 3.1 More Practice/Homework
Understand Fraction Division
Question 1.
Yu has a part of an hour for his workout. He would like to do a different exercise each \(\frac{1}{4}\) hour. How many different exercises does he have time for?

Answer:
3 different exercises,
Explanation:
Given Yu has \(\frac{3}{4}\) an hour for his workout.
He would like to do a different exercise each
\(\frac{1}{4}\) hour. Number of
different exercises does he have time for is
\(\frac{3}{4}\) ÷ \(\frac{1}{4}\) =
\(\frac{3}{4}\) X \(\frac{4}{1}\) =
\(\frac{3 X 4}{4 X 1}\) = 3.
Question 2.
A phone has \(\frac{5}{8}\) of its battery charge left. If the battery loses \(\frac{3}{8}\) of its full charge every hour, how many hours will the battery last?
_________________
Answer:
1\(\frac{2}{3}\) hours will the battery last,
Explanation:
Given a phone has \(\frac{5}{8}\) of its battery
charge left. If the battery loses \(\frac{3}{8}\) of
its full charge every hour, Number of hours will the battery last is
\(\frac{5}{8}\) ÷ \(\frac{3}{8}\) =
\(\frac{5}{8}\) X \(\frac{8}{3}\) =
\(\frac{5 X 8}{8 X 3}\) = \(\frac{5}{3}\)
as numerator is greater than denominator we write in
mixed fraction as 1\(\frac{2}{3}\) hours.
Question 3.
Sonia takes a \(\frac{4}{5}\)-mile walk every day. What part of her walk has she completed once she has walked \(\frac{3}{5}\) mile?
Answer:
1\(\frac{1}{3}\) part of her walk,
Explanation:
Given Sonia takes a \(\frac{4}{5}\)-mile walk every day.
The part of her walk has she completed once she has
walked \(\frac{3}{5}\) mile is
\(\frac{4}{5}\) ÷ \(\frac{3}{5}\) =
\(\frac{4}{5}\) X \(\frac{5}{3}\) =
\(\frac{4 X 5}{5 X 3}\) = \(\frac{4}{3}\)
as numerator is greater than denominator we write in
mixed fraction as 1\(\frac{1}{3}\) part.
Question 4.
Reason A bread recipe requires that \(\frac{5}{8}\) teaspoon of yeast be added to flour and water. Alejandro only has a \(\frac{1}{8}\)-teaspoon measuring spoon. How many measuring spoons of yeast will he need to add to the flour and water? Explain your reasoning.
________________________
________________________
Answer:
5 spoons,
Explanation:
Given a bread recipe requires that \(\frac{5}{8}\)
teaspoon of yeast be added to flour and water.
Alejandro only has a \(\frac{1}{8}\)-teaspoon
measuring spoon. Number of measuring spoons of yeast
will he need to add to the flour and water are
\(\frac{5}{8}\) ÷ \(\frac{1}{8}\) =
\(\frac{5}{8}\) X \(\frac{8}{1}\) =
\(\frac{5 X 8}{8 X 1}\) = 5 spoons.
Question 5.
Open Ended Write and solve a real-world problem that can be modeled by the division expression \(\frac{8}{12}\) ÷ \(\frac{9}{12}\). Identify what the dividend, divisor, and
quotient represent in your problem. Show your work.
Answer:
World problem:
“Joy has \(\frac{8}{12}\) candies and
Nancy has \(\frac{9}{12}\) more candies than Joy,
how many more candies does Nancy has than Joy”,
Dividend: \(\frac{8}{12}\),
Divisor : \(\frac{9}{12}\),
Quotient : \(\frac{8}{9}\),
Nancy has \(\frac{8}{9}\) more candies than Joy,
Explanation:
Wrote and solved a real-world problem that can be
modeled by the division expression
\(\frac{8}{12}\) ÷ \(\frac{9}{12}\).
Identified the dividend, divisor and quotient represented
in the problem as world problem –
“Joy has \(\frac{8}{12}\) candies and
Nancy has \(\frac{9}{12}\) more candies than Joy,
how much more does Nancy has more than Joy”,
more candies does
Dividend: \(\frac{8}{12}\),
Divisor : \(\frac{9}{12}\),
Quotient : \(\frac{8}{9}\), Now solving
\(\frac{8}{12}\) ÷ \(\frac{9}{12}\) =
\(\frac{8}{12}\) X \(\frac{12}{9}\) =
\(\frac{8 X 12}{12 X 9}\) = \(\frac{8}{9}\),
therefore Nancy has \(\frac{8}{9}\)
more candies than Joy.
Test Prep
Question 6.
Jolene is cutting a strip of yarn that is \(\frac{11}{12}\) inch long into pieces that are \(\frac{2}{12}\) inch long for a collage. How many complete pieces can she make?
Answer:
5 complete pieces Jolene can make,
Explanation:
Given Jolene is cutting a strip of yarn that is
\(\frac{11}{12}\) inch long into pieces
that are \(\frac{2}{12}\) inch long for a collage.
Number of complete pieces can she make are
\(\frac{11}{12}\) ÷ \(\frac{2}{12}\) =
\(\frac{11}{12}\) X \(\frac{12}{2}\) =
\(\frac{11 X 12}{12 X 2}\) = \(\frac{11}{2}\),
as numerator is greater than denominator we write in
mixed fraction as 5\(\frac{1}{2}\) therefore
5 complete pieces Jolene can make.
Question 7.
Sinh has \(\frac{14}{16}\) pound of nuts. He separates them into \(\frac{2}{16}\)-pound servings. How many servings can he make? Which expression models the situation?
A. \(\frac{2}{16}\) ÷ \(\frac{14}{16}\)
B. \(\frac{2}{16}\) × \(\frac{14}{16}\)
C. \(\frac{14}{16}\) ÷ \(\frac{2}{16}\)
D. \(\frac{14}{16}\) – \(\frac{2}{16}\)
Answer:
C. \(\frac{14}{16}\) ÷ \(\frac{2}{16}\),
Explanation:
Given Sinh has \(\frac{14}{16}\) pound of nuts.
He separates them into \(\frac{2}{16}\)-pound
servings. Number of servings can he make is the
expression models the situation is
\(\frac{14}{16}\) ÷ \(\frac{2}{16}\)
so matches with bit C. \(\frac{14}{16}\) ÷ \(\frac{2}{16}\).
Question 8.
Which question can be answered using the expression \(\frac{3}{8}\) ÷ \(\frac{5}{8}\) ?
A. How many \(\frac{5}{8}\)-cup servings of apple cider are in \(\frac{3}{8}\) cup of cider?
B. How many \(\frac{3}{8}\)-cup servings of apple cider are in \(\frac{5}{8}\) cup of cider?
C. Dan drank \(\frac{3}{8}\) of a \(\frac{5}{8}\)-cup serving of apple cider. How much did he drink?
D. Dan drank \(\frac{5}{8}\) of a \(\frac{3}{8}\)-cup serving of apple cider. How much did he drink?
Answer:
Bits B and D,
Explanation:
Given to find questions can be answered using the expression
\(\frac{3}{8}\) ÷ \(\frac{5}{8}\) are
bit A. How many \(\frac{5}{8}\)-cup servings of
apple cider are in \(\frac{3}{8}\) cup of cider? and
bit D. Dan drank \(\frac{5}{8}\) of a
\(\frac{3}{8}\)-cup serving of apple cider. How much did he drink?.
Question 9.
Terell is cutting a piece of trimming that is \(\frac{15}{18}\) foot long into pieces that are \(\frac{3}{18}\) foot long. How many pieces will Terell have?
A. 3 pieces
B. 5 pieces
C. 6 pieces
D. 8 pieces
Answer:
B. 5 pieces,
Explanation:
Given Terell is cutting a piece of trimming that is
\(\frac{15}{18}\) foot long into pieces that are
\(\frac{3}{18}\) foot long. Number of pieces will
Terell have \(\frac{15}{18}\) ÷ \(\frac{3}{18}\) =
\(\frac{15}{18}\) X \(\frac{18}{3}\) =
\(\frac{15 X 18}{18 X 3}\) = 5, Matches with bit
B. 5 pieces.
Spiral Review
Question 10.
What is the absolute value of -8?
_________________
Answer:
8,
Explanation:
The absolute value is the non-negative value of a
real number without regard for its sign so the
absolute value of -8 is 8.
Question 11.
Write an inequality to compare the integers -5 and -6.
_________________
Answer:
-5 > -6,
Explanation:
As – 5 is greater than -6 so an inequality to
compare the integers -5 and -6 is -5 > -6.
Question 12.
Find the product: \(\frac{2}{3}\) × \(\frac{3}{8}\).
Answer:
\(\frac{1}{4}\),
Explanation:
Given to find the product
\(\frac{2}{3}\) X \(\frac{3}{8}\) so it is
\(\frac{2 X 3}{3 X 8}\) = \(\frac{1}{4}\).