Into Math Grade 6 Module 2 Lesson 3 Answer Key Find and Apply LCM and GCF

We included HMH Into Math Grade 6 Answer Key PDF Module 2 Lesson 3 Find and Apply LCM and GCF to make students experts in learning maths.

HMH Into Math Grade 6 Module 2 Lesson 3 Answer Key Find and Apply LCM and GCF

I Can find and use the GCF or LCM to solve problems.

Step It Out

1. Three runners leave the starting line at the same time. Lena runs each lap in 3 minutes, Aria runs each lap in 5 minutes, and Tran runs each lap in 6 minutes. When is the first time, in minutes, that all three runners will cross the starting line together?
Answer:
30 minutes.

Explanation:
LCM of 3, 5, 6
3 = 3 × 1
5 = 5 × 1
6 = 2 × 3
So the LCM of 3, 5, 6 is 3 × 5 × 2 = 30
The first time that all three runners will cross the starting line together is 30 minutes.

Connect to Vocabulary
You have seen that a multiple of a number is the product of the number and any whole
number except 0. A least common multiple (LCM) is the least number that is a multiple of two or more given numbers.

A. How many minutes does it take Lena to run 12 laps?

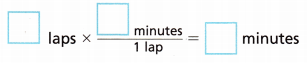
Answer:
12 minutes.
B. Complete the table.

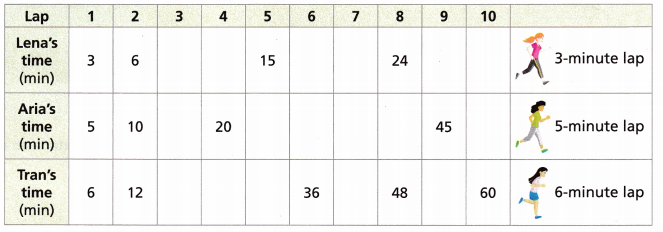
Answer:

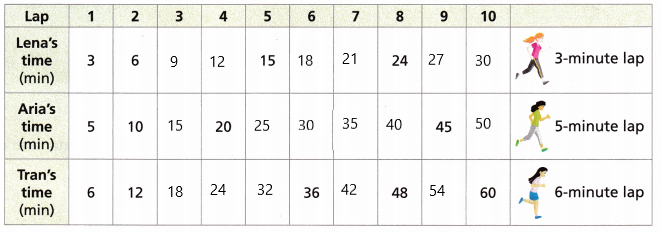
C. Look at the results in the table. What do you notice about the times in each row? __________________________
D. Look at the rows for the three runners. Do they have any time in common? If so, what is it? ________________
The first time in minutes that all three runners finish a lap at the same time is the least common multiple of their times.
____ is the least common multiple of ____, ___, and ____.

Turn and Talk If you extended the table, what would the next common multiple be? What pattern do you notice in the common multiples?

2. Taylor and Jake are in charge of bringing snacks for their chess club. They have 24 granola bars and 16 water bottles. They want to set out the snacks so that the snacks are distributed evenly in snack packs with no granola bars or water bottles left over. What is the greatest number of snack packs that Taylor and Jake can make?
Answer:
8

Explanation:
GCF of 24 and 16
24 = 2 × 12 = 3 × 8 = 4 × 6
16 = 2 × 8 = 4 × 4
The greatest number of 24  and 16 is 8

Connect to Vocabulary
You know that a factor is a number that is multiplied by another number to get a product. A greatest common factor (GCF) is the largest common factor of two or more given numbers.

A. Complete the tables to find the possible numbers of snack packs and numbers of granola bars and water bottles in each snack pack.

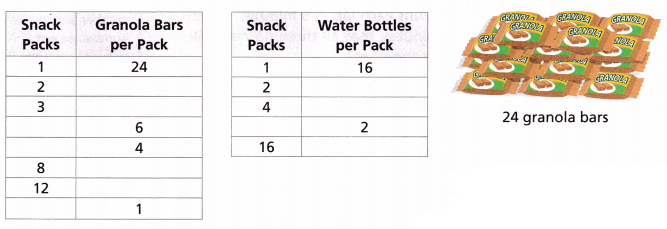
B. In the first table, the numbers of snack packs and the numbers of granola bars per pack are factors of ______
In the second table, the numbers of snack packs and the numbers of water bottles per pack are factors of _____.

Using the tables, list all the possible numbers of snack packs for each item.
Granola Bars: _______
Water Bottles: ________
C. What numbers occur in both lists? __________
D. What is the greatest number of snack packs a volunteer can make?
______________
E. The greatest common factor of 24 and 16 is
Answer:
8

Explanation:
The greatest common factor of 24 and 16 is 8.
F. You can use the greatest common factor to write the total number of bottles of water and granola bars, 24 + 16, as a sum of products.
Number of snack items = Number of granola bars + Number of water bottles =
You can use the Distributive Property to write the total number of snack items as the product of the GCF and another sum.
snack items
Answer:
4(6 + 4).

Explanation:
Number of snack items = Number of granola bars + Number of water bottles
= 4 (6) + 4(4)

3. Which is greater, \(\frac{5}{6}\) or \(\frac{7}{10}\)?
Answer:
\(\frac{5}{6}\) > \(\frac{7}{10}\)

Explanation:
The number \(\frac{5}{6}\) is greater than \(\frac{7}{10}\).
A. Complete the lists of multiples of the denominators.

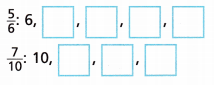
B. The least common multiple (LCM) of the numbers in the lists is ____.
C. Rewrite the fractions using the LCM as the common denominator.

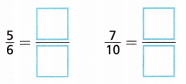
D. Use the new fractions to write an inequality to compare the original fractions.

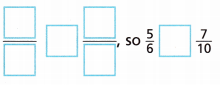
4. Which is greater: –\(\frac{13}{24}\) or –\(\frac{7}{18}\)?
A. Complete the lists of multiples for the denominators.

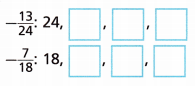
B. The least common multiple (LCM) of the numbers in the lists is _____.
C. Rewrite the fractions using the LCM of the denominators and complete the inequality to compare the original fractions.

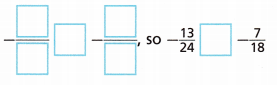
D. How would you compare the numbers using –\(\frac{1}{2}\) as a benchmark?
__________________________
__________________________

Check Understanding

Question 1.
Paper cups are sold in packages of 6, and napkins are sold in packages of 8. Ted wants to buy the same number of each. What is the least number of cups and napkins he needs to buy?
______________________________
Answer:
24

Explanation:
LCM of the given question is
6 × 1 = 6             8 × 1 = 8
6 × 2 = 12           8 × 2 = 16
6 × 3 = 18           8 × 3 = 24
6 × 4 = 24
The LCM of 6 and 8 is 24.

Question 2.
A florist has 60 tulips and 72 daffodils. The florist will make bouquets with the same number of tulips and the same number of daffodils in each using all the flowers. What is the greatest number of bouquets the florist can make?
_______________________________

Answer:
12

Explanation:

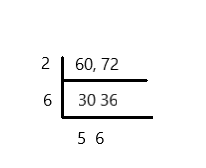
2 × 6 = 12
So the greatest number of bouquets the florist can make is 12.

Question 3.
Which is greater, \(\frac{11}{16}\) or \(\frac{24}{32}\) ? __________________
Answer:
\(\frac{24}{32}\) > \(\frac{11}{16}\).

Explanation:
The number \(\frac{24}{32}\) is greater than \(\frac{11}{16}\)

On Your Own

Question 4.
Jamie makes plates and bowls. She needs to ship 48 plates and 54 bowls to a store. She wants to ship the same number of items in each box. Plates and bowls are shipped separately.
Answer:
There are 8 plates and 9 bowls in each box.
Plates and bowls are shipped separately in each box.
Jamie wants to ship the same number of items in each box

Explanation:
Given,
Jamie needs to ship 48 plates and 54 bowls to a store. Plates and bowls are shipped separately.
Since there are 48 plates and 54 bowls
The highest common factor of 48 and 54 is 6.
Plates in each box = \(\frac{48}{6}\) = 8 plates
Bowls in each box = \(\frac{54}{6}\) = 9 bowls
Therefore there are 8 plates and 9 bowls in each box and there are 6 separate boxes.

A. What is the greatest number of items she can ship in each box?
_______________________
Answer:
6

Explanation:
The greatest number of items she can ship in each box is 6.

B. How many boxes of items will Jamie ship if she ships the greatest number possible in each box?
Boxes of plates: Boxes of bowls:
Answer:
8, 9

Explanation:
Boxes of plates are 8
Boxes of bowls are 9

C. Use Structure What is the greatest common factor of 48 and 54? Use the greatest common factor to write the total number of plates and bowls as a sum of products. Then use the distributive property to write the total number of items as a product.
Answer:
GCF of 48 and 54 are 6.

Question 5.
Grant is making muffins for a reunion. The recipe for blueberry muffins makes 12 muffins. The recipe for bran muffins makes 18 muffins. He wants to make the same number of each kind of muffin using only full recipes of each.
A. What is the least number of each type of muffin Grant can make?
_______________________
Answer:
66.667% or 0.6667

Explanation:
Based on the given conditions calculate 12 ÷ 18
\(\frac{2}{3}\)
Therefore the result is 66.667% or 0.6667

B. How many batches of each recipe will Grant make if he makes the least number of each type of muffin possible?
Blueberry: ___ batches Bran: ___ batches
Answer:
3 blueberry batches and 2 Bran batches.

Question 6.
A year is \(\frac{1}{3}\) of the lifespan of a fire ant queen. A year is \(\frac{1}{30}\) of a termite queen’s lifespan. Write an inequality to compare the fractions of the insects’ lifespans that a year represents.

Answer:
\(\frac{1}{3}\) > \(\frac{1}{30}\)

Explanation:
By comparing the fractions of the insects’ lifespans the lifespan of a fire ant queen \(\frac{1}{3}\) is greater than termite queen’s lifespan \(\frac{1}{30}\).

Question 7.
Reason Cameron and Tatiana volunteer at the public library. Cameron shelves one book every \(\frac{1}{4}\) minute. Tatiana shelves one book every \(\frac{3}{10}\) minute. Who is quicker at shelving books? Explain how you found your answer.
__________________________
__________________________
__________________________
Answer:
Cameron is quicker at shelving books.

Explanation:
Cameron shelves one book every \(\frac{1}{4}\) and Tatiana shelves one book every \(\frac{3}{10}\).
So \(\frac{1}{4}\) = \(\frac{10}{40}\) = \(\frac{5}{20}\)
\(\frac{3}{10}\) = \(\frac{12}{40}\) = \(\frac{6}{20}\)
\(\frac{6}{20}\) > \(\frac{5}{20}\).
So, Cameron is quicker at shelving books.

Question 8.
Darnell helps to make lunches at a picnic. Each picnic basket will have the amounts of ham salad and potato salad shown in the illustration. Which is greater, the amount of ham salad or the amount of potato salad? Show your work.

__________________
Answer:
\(\frac{9}{12}\) > \(\frac{8}{16}\)

Explanation:
Given,
Ham salad = \(\frac{8}{16}\)
Potato salad = \(\frac{9}{12}\)
by comparing the both lunches, the amount of potato salad is greater than Ham salad.
\(\frac{9}{12}\) > \(\frac{8}{16}\).

Question 9.
Critique Reasoning Ryan is making biscuits. The recipe calls for 0.25 quart of milk and 2.5 cups of flour. He has \(\frac{1}{5}\) quart of milk and \(\frac{9}{4}\) cups of flour. Ryan makes the recipe with the milk and flour that he has. Explain his error.
__________________________
__________________________
Answer:
Ryan does not have enough milk to make biscuits.

Explanation:
Given the recipe calls for 0.25 quarts of milk and 2.5 cups of flour. So Ryan does not have enough milk. He only has only 0.2 quarts of milk to make biscuits.

Question 10.
Use the LCM to find a common denominator for the fractions \(\frac{3}{8}\) and \(\frac{1}{10}\). Write the fractions with the new denominator. Then write an inequality
involving the rewritten fractions to show which is greater.
Answer:

Question 11.
Groups of sixth graders and seventh graders compete in a race. The contestants include \(\frac{3}{4}\) of the sixth graders and \(\frac{4}{5}\) of the seventh graders. Which group has a greater fraction of their grade represented?
Answer:
Given,
\(\frac{3}{4}\) of the sixth graders = 0.75
\(\frac{4}{5}\) of the seventh graders = 0.8
The seventh graders group has a greater fraction of the given data represented.
\(\frac{4}{5}\) > \(\frac{3}{4}\)

Question 12.
Open Ended How can you determine which of the numbers below is greatest?
\(\frac{13}{20}\), \(\frac{5}{8}\), \(\frac{3}{5}\), \(\frac{3}{10}\)
Answer:
\(\frac{13}{20}\) is the greatest number.

Explanation:
From the given question the number \(\frac{13}{20}\) is greater than the other numbers.
0.65, 0.625, 0.6, 0.3

Question 13.
The table shows the rainfall in four towns on the same day. Which town had more rain, Brighton or Springfield? Morristown or Pine Grove?

Answer:
Springfield

Explanation:
The town of Springfield had more rain than any other town.

Question 14.
Use Structure The table shows the distance below ground of items found at an archaeological site. Researchers also found a mouse fossil at the same site. Which, if any, of the items in the table were a greater distance below ground than the mouse fossil?


_______________________
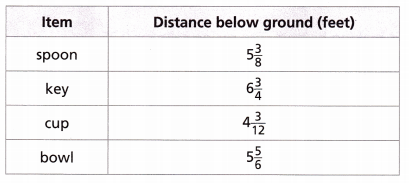
Answer:

Find the LCM of the number pair.

Question 15.
8 and 4
_______________________
Answer:
LCM = 2 × 2 × 2
LCM = 8

Explanation:

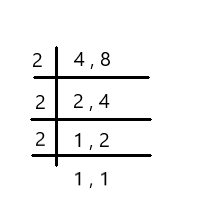
Question 16.
5 and 12
_______________________
Answer:
60

Explanation:
The LCM of 5 and 12 is 60
5 × 12 = 60.

Question 17.
4 and 9
_______________________
Answer:
36

Explanation:

 

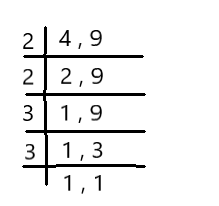
LCM  = 2 × 2 × 3 × 3
LCM = 36

Question 18.
6 and 21
_______________________
Answer:
42

Explanation:

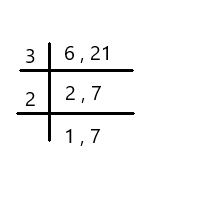
LCM of 6 and 21 is 3 × 2 × 1 × 7 = 42.

Question 19.
15 and 9
_______________________
Answer:
45

Explanation:

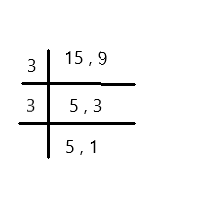
LCM of 15 and 9 is 3 × 3 × 5 × 1 = 45

Question 20.
20 and 8
_______________________
Answer:
40

Explanation:

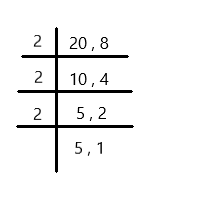
LCM of 20 and 8 is 2 × 2 × 2 × 5 × 1 = 40

Find the GCF of the number pair.

Question 21.
16 and 30
_______________________
Answer:

Question 22.
24 and 32
_______________________
Answer:

Question 23.
26 and 39
_______________________
Answer:

Question 24.
28 and 14
_______________________
Answer:

Question 25.
32 and 40
_______________________
Answer:

Question 26.
54 and 36
_______________________
Answer:

Complete the inequality using the symbol > or <.

Question 27.
\(\frac{4}{10}\) \(\frac{5}{6}\)
Answer:
<

Explanation:
\(\frac{4}{10}\) < \(\frac{5}{6}\)

Question 28.
\(\frac{3}{33}\) \(\frac{40}{100}\)
Answer:
>

Explanation:
\(\frac{3}{33}\) > \(\frac{40}{100}\)

Question 29.
\(\frac{5}{12}\) \(\frac{3}{20}\)
Answer:
>

Explanation:
\(\frac{5}{12}\) > \(\frac{3}{20}\)

Write an inequality to compare the fractions.

Question 30.
\(\frac{24}{18}\) and \(\frac{25}{15}\)
Answer:
\(\frac{24}{18}\) < \(\frac{25}{15}\)

Explanation:
The inequality to compare the given fractions is \(\frac{24}{18}\) < \(\frac{25}{15}\)

Question 31.
\(\frac{3}{8}\) and –\(\frac{5}{7}\)
Answer:
\(\frac{3}{8}\) < \(\frac{5}{7}\)

Explanation:
The inequality to compare the given fractions is \(\frac{3}{8}\) < \(\frac{5}{7}\)

Question 32.
\(\frac{18}{42}\) and –\(\frac{15}{21}\)
Answer:
\(\frac{18}{42}\) < \(\frac{15}{21}\).

Explanation:
The inequality to compare the given fractions is \(\frac{18}{42}\) < \(\frac{15}{21}\).

Question 33.
\(\frac{12}{16}\) and \(\frac{16}{24}\)
Answer:
\(\frac{12}{16}\) > \(\frac{16}{24}\)

Explanation:
The inequality to compare the given fractions is \(\frac{12}{16}\) > \(\frac{16}{24}\)

Question 34.
\(\frac{5}{12}\) and \(\frac{11}{28}\)
Answer:
\(\frac{5}{12}\) > \(\frac{11}{28}\).

Explanation:
The inequality to compare the given fractions is \(\frac{5}{12}\) > \(\frac{11}{28}\).

Question 35.
\(\frac{7}{10}\) and –\(\frac{5}{9}\)
Answer:
\(\frac{7}{10}\) > \(\frac{5}{9}\).

Explanation:
The inequality to compare the given fractions is \(\frac{7}{10}\) > \(\frac{5}{9}\).

Lesson 2.3 More Practice/Homework

Find and Apply LCM and GCF

Question 1.
Model with Mathematics Martha ran \(\frac{5}{8}\) of a mile and Terry ran \(\frac{6}{15}\) of a mile on the weekend. Who ran a larger portion of a mile? Write an inequality to compare the portions of a mile.
Answer:
Martha ran a larger portion of mile.
\(\frac{75}{120}\) > \(\frac{48}{120}\)

Explanation:
Let us solve the given question
\(\frac{5}{8}\) = \(\frac{5× 15}{8 × 15}\) = \(\frac{75}{120}\)
\(\frac{6}{15}\) = \(\frac{6 × 8}{15 × 8}\) = \(\frac{48}{120}\)
\(\frac{75}{120}\) > \(\frac{48}{120}\)
0.625 > 0.4
So Martha ran a larger portion of the mile.

Question 2.
Reason A radio station is giving away concert tickets to every 60th caller and a concert T-shirt to every 45th caller. What will be the number of the first caller to get both items? Explain.
Answer:
The number of the first caller to get both items is 180.

Explanation:
Given a radio station is giving away concert tickets to every 60th caller.
And giving concert T-shirts to every 45th caller.
So the number of the first caller to get both items will be the LCM of 60and 45.
60 = 2 × 2 × 3 × 5
45 = 3 × 3 × 5
so LCM of 60 and 45 = 2 × 2 × 3 × 3 × 5
= 180

Question 3.
A cuckoo clock has birds that pop out of their nests every 6 minutes and dancers that pop out every 15 minutes. The birds and dancers have just popped out at the same time. When will this happen again in the next 60 minutes?
Answer:
30 minutes and 60 minutes.

Explanation:
From the question,
6 = 2 × 3
15 = 3 × 5
2 × 3 × 5 = 30 minutes.
30 × 2 = 60 minutes.

Question 4.
String-cheese sticks are sold in packs of 10 and celery sticks in packs of 15. Mr. Deluca wants to give each of 30 students one string-cheese stick and one celery stick. What is the least number of packs he should buy so there are none left over?
Answer:
3 packs of string cheese and 2 packs of celery.

Explanation:
String-cheese sticks are sold in packs of 10 and celery sticks in packs of 15.
Mr. Deluca wants to give each of the 30 students one string-cheese stick and one celery stick.
30 ÷ 10 = 3
30 ÷ 15 = 2
so, for string cheese ht least number is 3, and for celery sticks, the least number is 2. Therefore the answer is 3, 2

Math on the Spot Find the GCF of each set of numbers.

Question 5.
8 and 12
Answer:
GCF of 8 and 12 is 4
Factors of 8 = 1, 2 , 4, 8
Factors of 12 = 1, 2, 3, 4, 6 and 12.

Question 6.
10, 15, and 30
Answer:
10, 15, and 30 are 5.

Explanation:
Factors of 10 = 1, 2, 5, 10
factors of 15 = 1, 3, 5, and 15
Factos of 30 = 1, 2, 3, 5, 6, 10, 15 and 30

Question 7.
18, 36, and 60
Answer:
GCF of 8 and 12 is 12.

Explanation:
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Hence GCF of 8 and 12 is 12.

Question 8.
Use the GCF of 48 and 30 to write the sum of the two numbers as the product of their GCF and another sum.

Answer:
48 = 6 × 8
30 = 6 × 5
48 + 30 = 6 (8) + 6 (5) = 6 (8 + 5) = 6 (13).

Explanation:

For Problems 9—11, compare the fractions using the LCM.

Question 9.
\(\frac{1}{7}\), \(\frac{2}{3}\)
Answer:
\(\frac{1}{7}\) < \(\frac{2}{3}\)

Explanation:
Given fractions are \(\frac{1}{7}\), \(\frac{2}{3}\)
LCM of 7 and 3 is 21.
Now convert each one of \(\frac{1}{7}\), \(\frac{2}{3}\) into an equivalent fraction having 21 as denominator.
\(\frac{1}{7}\) = \(\frac{1× 3}{7 × 3}\) = \(\frac{3}{21}\)
\(\frac{2}{3}\) = \(\frac{2 × 7}{3 × 7}\) = \(\frac{14}{21}\)
Its shows \(\frac{3}{21}\) < \(\frac{14}{21}\)
Hence \(\frac{1}{7}\) < \(\frac{2}{3}\).

Question 10.
\(\frac{3}{5}\), \(\frac{1}{4}\)
Answer:
\(\frac{3}{5}\) > \(\frac{1}{4}\).

Explanation:
Given fractions are \(\frac{3}{5}\), \(\frac{1}{4}\)
LCM of 5 and 4 is 20.
Now convert each one of \(\frac{3}{5}\), \(\frac{1}{4}\) into an equivalent fraction having 20 as denominator.
\(\frac{3}{5}\) = \(\frac{3× 4}{5 × 4}\) = \(\frac{12}{20}\)
\(\frac{1}{4}\) = \(\frac{1 × 5}{4 × 5}\) = \(\frac{5}{20}\)
Its shows \(\frac{12}{20}\) > \(\frac{5}{20}\)
Hence \(\frac{3}{5}\) > \(\frac{1}{4}\).

Question 11.
\(\frac{4}{6}\), \(\frac{4}{8}\)
Answer:
Given fractions are \(\frac{4}{6}\), \(\frac{4}{8}\)
LCM of 6 and 8 is 24.
Now convert each one of \(\frac{4}{6}\), \(\frac{4}{8}\) into an equivalent fraction having 24 as denominator.
\(\frac{4}{6}\) = \(\frac{4× 4}{6 × 4}\) = \(\frac{16}{24}\)
\(\frac{1}{4}\) = \(\frac{1 × 6}{4 × 6}\) = \(\frac{6}{24}\)
Its shows \(\frac{16}{24}\) > \(\frac{6}{24}\)
Hence \(\frac{4}{6}\) > \(\frac{4}{8}\).

For Problems 12-14, compare the fractions.

Question 12.
\(\frac{10}{14}\), \(\frac{3}{7}\)
Answer:
\(\frac{10}{14}\) is greater than \(\frac{3}{7}\)

Explanation:
The given number \(\frac{10}{14}\) is greater than \(\frac{3}{7}\).
\(\frac{10}{14}\) > \(\frac{3}{7}\).

Question 13.
–\(\frac{14}{21}\), –\(\frac{3}{9}\)
Answer:
Greater than

Explanation:
The given number \(\frac{14}{21}\) is greater than the number \(\frac{3}{9}\).

Question 14.
\(\frac{30}{20}\), \(\frac{8}{2}\)
Answer:
less than

Explanation:
\(\frac{30}{20}\) < \(\frac{8}{2}\)

Test Prep

Question 15.
Which expression shows the sum of 72 and 96 as the product of the GCF and a sum of two numbers with no common factor?
A. 12(6 + 8)
B. 24(3 + 4)
C. 24(6 + 8)
D. 48(3 + 4)
Answer:
The answer is Choice B: 24(3 + 4).

Explanation:
From the given question we are required to calculate the expression that shows the sum of 72 and 96 as the prodcut of the GCF and a sum of two numbers with no common factors.
The factors of 72 are
2 × 2 × 2 × 3 × 3
The factors of 96 are
2 × 2 × 2 × 2 × 2 × 3
The factors that are in common to 72 and 96  are 2 × 2 × 2 × 3  and therefore gives a total of 24 which is the GCF of 72 and 96. The remaining factor of 72 and 96 are 3 and 4 respectively. And, since 3 and 4 have no common factor, Therefore, the expression which shows the sum of 72 and 96 as the product of the GCF and a sum of two numbers with no common factor is 24(3 + 4).

Question 16.
Write an inequality to compare the numbers 12.7 and 12\(\frac{3}{4}\).
Answer:
The inequality for the given numbers is <.

Explanation:
The given numbers are 12.7 and 12\(\frac{3}{4}\) = \(\frac{51}{4}\) = 12.75.
12.7 < 12.75.

Question 17.
Ambrose and Kaitlin are volunteering at a food bank. They both start at the same time. Kaitlin takes 13 minutes to pack a box with donated food. Ambrose takes 7 minutes to pack a box. After how many minutes will they finish packing boxes at the same time?
Answer:
After 91 minutes.

Explanation:
Kaitlin takes 13 minutes to pack a box and ambrose takes 7 minutes.
They finish packing boxes at the same time is 13 × 7 = 91 minutes.

Question 18.
Jewel has 20 apples and 16 bananas that she wants to arrange in baskets. There needs to be the same number of apples and the same number of bananas in each basket. What is the greatest number of baskets she can make? How many apples and bananas will be in each basket?
Answer:
16 baskets.

Explanation:
From the given question we have equal number of apples and bananas in each basket. The greatest number of basket jewel can make will be 16 baskets.

Spiral Review

Question 19.
Write an inequality to compare the numbers.
-13 and -10
________________
Answer:
-13 is greater than -10.
-13 > -10

Explanation:
By comparing the numbers the inequality we can write is -13 > -10.

Question 20.
Write the list of numbers in order from least to greatest.
5, -6, 4, -3, 8, 7, -5
Answer:
-3, -5, -6, 4, 5, 7, 8

Explanation:
The list of numbers in order from least to greatest are -3, -5, -6, 4, 5, 7, 8.

Question 21.
Which number, -12 or -18, has the greater absolute value?
__________________
Answer:
-18

Explanation:
The number -18 has the greater absolute value.