Into Math Grade 6 Module 13 Lesson 3 Answer Key Solve Volume Problems

We included HMH Into Math Grade 6 Answer Key PDF Module 13 Lesson 3 Solve Volume Problems to make students experts in learning maths.

HMH Into Math Grade 6 Module 13 Lesson 3 Answer Key Solve Volume Problems

I Can use the formula V = lwh to find the volume or an unknown dimension of a rectangular prism.

Step It Out

Question 1.
Lyon is making a toolbox as shown.

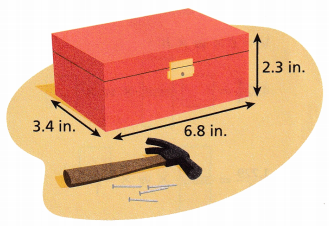
A. What are the dimensions of the box?
Length: _____________
Width: _____________
Height: _____________
Answer:
Length = 3.4 in
Width = 6.8 in
Height = 2.3 in

Explanation:
From the given figure we can measure the dimensions of the box.
The dimensions of the box are l = 3.4 in, w = 6.8 in and H = 2.3 in

B. Complete the volume equation.
V = l × w × h = × ×
Answer:
V = l × w × h = 3.4 × 6.8 × 2.3

Explanation:
Given,
l = 3.4 in, w = 6.8 in and H = 2.3 in
V = l × w × h = 3.4 × 6.8 × 2.3

C. What is the volume of the box?
_________ cubic inches, or _________ in³
Answer:
53.17 cubic inches or in³

Explanation:
Given,
l = 3.4 in, w = 6.8 in and H = 2.3 in
V = l × w × h
= 3.4 × 6.8 × 2.3
= 53.17 cubic inches or in³

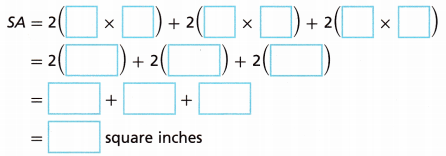
D. Lyon wants to paint the toolbox. To do so, he needs to know the surface area of the toolbox. Find the surface area of the toolbox.

Answer:
The surface area of the toolbox is = 61.88 square inches.

Explanation:
Given,
l = 3.4 in, w = 6.8 in and H = 2.3 in
Surface area = 2 (wl+hl+hw)
Surface area = 2 ((6.8 × 3.4) + (2.3 × 3.4) + (2.3 × 6.8))
Area = 2 ((23.12) + (7.82) + (15.64))
Area = 2 ( 30.94)
The surface area of the toolbox is = 61.88 square inches.

E. A tube of paint covers 40 square inches. How many tubes of paint should Lyon buy? Explain.
Answer:
Lyon bought 2 tubes of paint

Explanation:.
The surface area of the toolbox is = 61.88 square inches.
tube paint cover 40 square inches
Lyon bought \(\frac{61.88}{40}\) = 1.5 = 2 tubes of paint.

Turn and Talk Why do you think volume is measured in cubic units?
Answer:
While calculating the volume we need to multiply all three dimensions. Therefore, volume is measured in cubic units such as cubic meters, and cubic inches.

Question 2.
A company makes cereal boxes with a volume of 432\(\frac{1}{4}\) cubic inches. The dimensions of one of the cereal boxes is shown. What is the width of the box?

A. How can you find the volume of the cereal box?
Answer:
The volume of the cereal box = is 432.25 cubic inches.

Explanation:
Given,
Volume = 432\(\frac{1}{4}\) cubic inches
v = \(\frac{1729}{4}\)
The volume of the cereal box = is 432.25 cubic inches.

B. Complete the equation to find the volume of the cereal box.

V = L × w × h

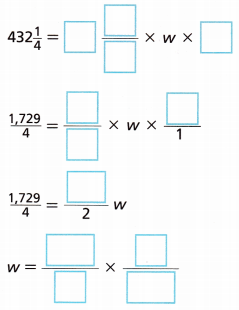
Answer:

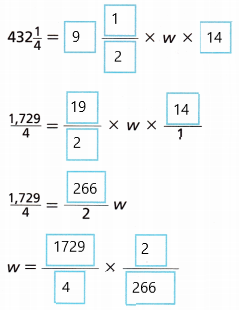
C. What is the width of the cereal box?
Answer:
3.25 inches

Explanation:

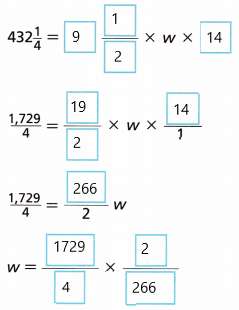
w = 3.25 inches

Turn and Talk In Task 2, if the width was given and the length was not, would the steps you used to find the length be different than the steps you used to find the width? Explain.
Answer:
The steps would be the same as we used to find the width.

Check Understanding

Question 1.
A right rectangular prism is 10.25 yards long, 5.5 yards wide, and 2 yards tall. What is the volume of the prism?
Answer:
112.75 cubic yards.

Explanation:
Given,
l = 10.25 yards, width = 5.5 yards and height = 2 yards
The volume of the prism is l × w × h
Volume = 10.25 × 5.5 × 2
Volume = 112.75 cubic yards.

Question 2.
A large rectangular shipping container has a volume of 12\(\frac{3}{8}\) cubic feet. The shipping container is 2\(\frac{1}{5}\) feet long and 2\(\frac{1}{2}\) feet wide. What is the height of the shipping container?
Answer:
The height of the shipping container = \(\frac{4}{9}\) feet.

Explanation:
Given,
Volume = 12\(\frac{3}{8}\) cubic feet = \(\frac{99}{8}\) cubic feet
Length = 2\(\frac{1}{5}\) feet = \(\frac{11}{5}\) feet
width = 2\(\frac{1}{2}\) feet wide = \(\frac{5}{2}\) feet wide
We need to find height of the shipping container.
Volume = l × w × h
Volume = \(\frac{11}{5}\) × \(\frac{5}{2}\) × h
\(\frac{99}{8}\) = \(\frac{11}{5}\) × \(\frac{5}{2}\) × h
h = \(\frac{11}{5}\) × \(\frac{5}{2}\) × \(\frac{8}{99}\)
h = \(\frac{4}{9}\) feet.

On Your Own

Question 3.
What is the volume of the puzzle cube?

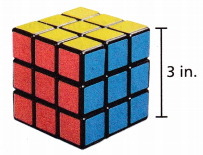
Answer:
The volume of the cube is 27 cubic inches.

Explanation:
The volume of a cube = S³
Given S = 3 in
The volume of the cube =  S × S × S
Volume = 3 × 3 × 3
The volume of the cube = is 27 cubic inches.

Question 4.
A fish tank is filled halfway with water.

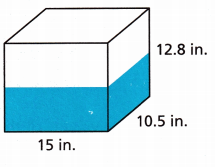
A. What is the volume of the tank?
Answer:
The volume of the tank is 2016 cubic inches.

Explanation:
Given,
l = 15 in, w = 10.5 in and h = 12.8 in
The volume of the tank = l × b × h
Volume = 15 × 10.5 × 12.8
Voulme = 2016 cubic inches.

B. What is the volume of the water in the tank?
Answer:
The volume of the tank = the volume of the water in the tank.

Question 5.
A concert poster is shipped in the box shown.

A. What is the volume of the poster box?
Answer:
The volume of the poster box is 179.52 cubic inches.

B. Show how you found your answer.
Answer:
Given,
l = 24 in, w = 3\(\frac{2}{5}\) = \(\frac{17}{5}\) and height = 2\(\frac{1}{5}\) = \(\frac{11}{5}\)
The volume of the tank = l × w × h
Volume = 24 × \(\frac{17}{5}\) × \(\frac{11}{5}\)
Volume of the poster box = \(\frac{4488}{25}\)
Volume = 179.52 cubic inches.

Question 6.
Carmen builds the dresser shown. The rectangular portion of the dresser has a volume of 27 cubic feet.

A. How can you find the missing dimension?
Answer:
The missing dimension is x
x = 1.5 ft

Explanation:
Given,
Volume = 27 cubic feet
l = 6 ft, w = x ft and h = 3 ft
Volume = l × w × h
Volume = 6 × x × 3
27 = 18 x
x = \(\frac{27}{18}\)
x = \(\frac{3}{2}\)
x = 1.5 ft

B. What is the missing dimension of the dresser?
Answer:
The missing dimension of the dresser is x which is the width of the figure.

Question 7.
Reason A set of dishes comes in a cube-shaped box that has a surface area of 600 square inches.

A. How do you find the surface area of a cube?
Answer:
The surface area of a cube is 600 square inches.

Explanation
Given,
The surface area of 600 square inches

B. What is the area of each face of the cube?
Answer:
Surface area = 6a²
600 = 6a²
a² = \(\frac{600}{6}\)
a² = 100
a = 10

C. What are the dimensions of the cube?
Answer:
a = 10 inches

D. What is the volume of the cube?
Answer:
The volume of the cube = 1000 cubic inches

Explanation:
The volume of the cube is a³
a = 10
Volume = 10³
Volume = 1000 cubic inches.

Question 8.
A toy company ships packages in large boxes. The toy package and the shipping box are shown.

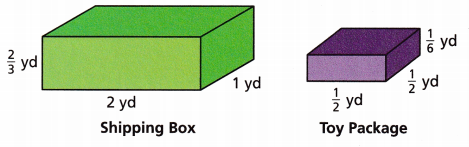
A. What is the volume of the shipping box?
Answer:
The volume of the shipping box is 1.33 cubic yd.

Explanation:
Given,
l = 2 yd, w = 1 yd and h = \(\frac{2}{3}\)
Volume of the shipping box = l × w × h
Volume = 2 × 1 × \(\frac{2}{3}\)
= \(\frac{4}{3}\)
= 1.33 cubic yard.

B. What is the volume of the toy package?
Answer:
The volume of the toy package is \(\frac{1}{24}\) cubic yards.

Explanation:
Given,
l = \(\frac{1}{2}\), w = \(\frac{1}{2}\) and h = \(\frac{1}{6}\)
The volume of the toy package  = l × w × h
= \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{6}\)
= \(\frac{1}{24}\) cubic yards.

C. How many toy packages could fit in the shipping box?
Answer:

D. Open-Ended Describe one way you can arrange the packages in the shipping box.
Answer:

Lesson 13.3 More Practice/Homework

Question 1.
Reason A cube-shaped box can be wrapped completely in gift wrap that measures 384 square inches. What is the volume of the box?
Answer:
Given,
The surface area of the cube is 384 square inches.
Surface area = 6a²
384 sq inches = 6a²
\(\frac{384}{6}\) = a²
a² = 64
a = 8
Volume = a × a × a
Volume = 8 × 8 × 8
Volume = 512 cubic inches.

Question 2.
STEM An architect builds a house like the one shown. What is the total volume of the house?

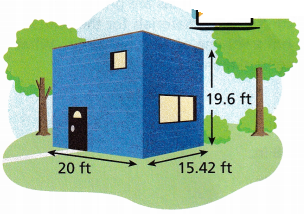
Answer:
Given,
l = 20 ft, w = 15.42 ft and h = 19.6 ft
The volume of the house = l × w × h
Volume = 20 × 15.42 × 19.6
The volume of the house is 6044 cubic ft.

Question 3.
An aquarium has a large fish tank with the dimensions shown. The tank has a volume of 585 cubic meters.

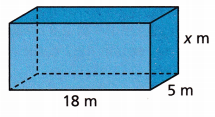
What is the depth of the tank?
Answer:
The depth of the tank is 6.5 m.
Given,
Volume = 585 cubic meters
l = 18 m and w = 5 m and depth = x m
Volume = l × w × d
Volume = 18 × 5 × x
585 = 18 × 5 × x
x = \(\frac{585}{90}\)
x = 6.5 m
Depth = 6.5 m

Question 4.
Joshua is organizing a garage using stackable containers like the one shown. He has a total of 12 containers. What is the combined total volume of the containers?

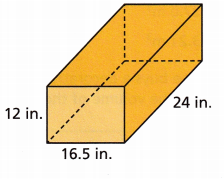
Answer:
The volume of the container is 4752 cubic inches.

Explanation:
Given,
l = 24 in, w = 16.5 in and h = 12 in
The volume of the containers is l × w × h
Volume = 24 × 16.5 × 12
Volume = 4752 cubic inches.

Question 5.

Math on the Spot Aubrey has a suitcase with a volume of 2200 cubic inches. The length of the 16.5 in. suitcase is 25 inches and the width is 11 inches. What is the height of Aubrey’s suitcase?
Answer:
The height of Aubrey’s suitcase is 12.12 inches.

Explanation:
Given,
Volume = 2200 cubic inches.
l = 16.5 in, w = 11 inches and we need to find the height
Volume = l × w × h
2200 = 16.5 × 11 × h
h = \(\frac{2200}{(16.5 × 11)}\) in.
h = 12.12 inches.

Question 6.
A rectangular prism has a length of 2\(\frac{3}{5}\) inches and a width of 1\(\frac{2}{5}\) inches. If the prism has a volume of 10\(\frac{23}{25}\) cubic inches, what is the height of the prism? Explain how you found your answer.
Answer:
The height of the prism is 0.33 inches.
Given,
l = 2\(\frac{3}{5}\) inches = \(\frac{13}{5}\) inches
w = 1\(\frac{2}{5}\) = \(\frac{7}{5}\)
Volume = 10\(\frac{23}{25}\) = \(\frac{273}{25}\)
Volume = l × w × h
\(\frac{273}{25}\) = \(\frac{13}{5}\) × \(\frac{7}{5}\) × h
h = \(\frac{7}{5}\) × \(\frac{13}{5}\) × \(\frac{25}{273}\)
h = \(\frac{(7×13×25)}{(5×5×273}\)
h = \(\frac{2275}{6825}\)
h = 0.33 inches.

Test Prep

Question 7.
Students in an art class are given boxes to use for storage for their materials for the year. Shaun’s box has a volume of 72 cubic inches. What is the unknown dimension?

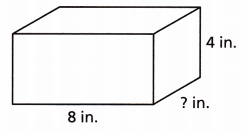
(A) 2\(\frac{1}{4}\) in.
(B) 9 in.
(C) 18 in.
(D) 60 in.
Answer:
2\(\frac{1}{4}\) in.

Explanation:
Given,
Volume = 72 cubic inches.
l = 8 in height = 4 in and w = ?
We need to find the width of the given box
The volume of the box is l × w × h
72 = 8 × w × 4
72 = 32 w
w = \(\frac{72}{32}\)
w = \(\frac{18}{8}\)
w = \(\frac{9}{4}\)
w = 2.25 inches.
w = 2\(\frac{1}{4}\) in.

Question 8.
A sculptor buys a block of marble shaped like a rectangular prism to use for a sculpture. The original block of marble had a length of 3.5 meters, a width of 4 meters, and a height of 2.8 meters. If the sculptor chisels away a volume of marble that equals 12.2 cubic meters, what is the volume of the resulting sculpture?
(A) 51.4 m³
(B) 39.2 m³
(C) 27.0 m³
(D) 3.21 m³
Answer:
3.21 m³

Explanation:
l = 3.5 m, width = 4 m and height = 2.8 m
The volume of marble equals = 12.2 cubic meters.
The volume of the original block is 3.5 × 4 × 2.8 = 39.2 cubic meters
\(\frac{39.2}{12.2}\) = 3.21 m³

Question 9.
Angelee buys a decorative photo box as shown. What is the volume of the photo box?

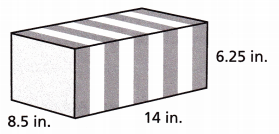
Answer:
The volume of the photo box is 743.75 cubic inches.

Explanation:
Given,
l = 8.5 in, w = 14 in and height = 6.25 in
The volume of the photo box is  l × w × h
Volume = 8.5 × 14 × 6.25
Volume = 743.75 cubic inches.

Spiral Review

Question 10.
What is the area of the triangle?

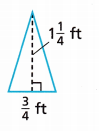
Answer:
Given,
base = \(\frac{3}{4}\) ft and height = 1\(\frac{1}{4}\) = \(\frac{5}{4}\)
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × \(\frac{3}{4}\) × \(\frac{5}{4}\)
Area = \(\frac{1 × 3 × 5}{2 × 4 × 4}\)
Area of the triangle is \(\frac{15}{32}\) square feet.

Question 11.
Evaluate the expression.
3² – 2² + 1
Answer:
The answer for the given expression is 6.

Explanation:
Let us solve the given expression
3² – 2² + 1
(3 × 3) – (2×2) +1
9 – 4 + 1
5 + 1
6.

Question 12.
Amanda earns $12 an hour babysitting. She spends $8 of her earnings on dinner later that evening. Write an expression to represent her total profit after babysitting for x hours and then eating dinner.
Answer:
$12x – $8

Explanation:
Given,
Amanda earns $12 an hour
Spends $8 on dinner
Now we need to calculate profit after babysitting for x hours.
$12 × x = $8
$12x – $8