We included HMH Into Math Grade 6 Answer Key PDF Module 13 Lesson 1 Explore Nets and Surface Area to make students experts in learning maths.
HMH Into Math Grade 6 Module 13 Lesson 1 Answer Key Explore Nets and Surface Area
I Can make and use nets to find the surface areas of rectangular and triangular prisms and pyramids.
Spark Your Learning
Caleb built a rectangular box to store his cast-iron oven when camping. He wants to paint the outside of the box, and has enough paint to cover an area of 14 square feet. Does Caleb have enough paint? Explain.


Answer:
N0, he does not have enough paint
If we find out the area of the rectangular solid
The volume of rectangular solid = L × W × H
Total Surface area of rectangular solid = 2(L × W + L × H + W × H)
length = 2.5; width = 1.5; height = 1ft
surface area = 2(2.5 x 1.5 + 2.5 x 1 + 1.5 x 1)
surface area = 2(7.75)
surface area = 15.5
Therefore, the paint is not sufficient to paint because he has a paint for 14 sq ft. But the area of the rectangular solid is 15.5 sq ft.
Turn and Talk If Caleb decides not to paint the bottom of the storage box, will he have enough paint to paint the storage box? Explain.
Answer: Yes, then he should have enough paint.
This means one side he should not paint then we can calculate like this:
3.75 + 8 = 11.75
What we did is avoided the bottom part in the calculation.
For the top part: 2.5 x 1.5 = 3.75
For the remaining parts = 2(L × H + W × H)
= 2(4) = 8
We added both values then we get 11.75 sq.ft
Build Understanding
Question 1.
A solid figure is a three-dimensional figure because it has three dimensions: length, width, and height.
Connect to Vocabulary
A net is an arrangement of two-dimensional figures that can be folded into a closed solid figure.
A. A cube is a closed three-dimensional figure. Look at the cube at the right. How many faces does a cube have?
Answer:
A cube is a three-dimensional shape that is defined XYZ plane. It has six faces, eight vertices and twelve edges. All the faces of the cube are in square shape and have equal dimensions.
B. A net is the pattern made when the surface of a closed three¬dimensional figure is laid out flat, showing each face of the figure. Look at the two nets shown. What do you notice about the nets? What three-dimensional figures might they represent? Explain.
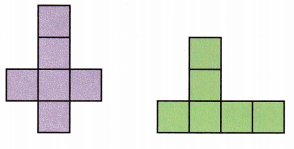
Answer: cube
Explanation:
Cut the papers in the given nets and fold them to check whether they are cubes or not. Definitely, the two nets will form a figure that is nothing but a cube.
C. Trace both nets in Part B on a separate sheet of paper. Cut out each net. Then fold the nets. Which net will fold into a closed three¬dimensional figure? What is the three-dimensional figure?
Answer:
When we fold the purple figure it is easily shown that it is a cube. And when we fold a green net it is overlapping.
Therefore, purple forms a cube.
D. Write an equation to represent the area of one face of the cube.
Answer: side x side = side^2
Explanation:
The definition of the surface area of a given cube states that the total surface area is equal to the sum of all the areas of the faces of the cube. Since the cube has six faces, therefore, the total surface area of the cube will be equal to the sum of all six faces of the cube.
Since the surface of the cube is in a square shape. Hence, the area of each face of the cube is equal to the square of the edge. Let the length of an edge of a cube is a.
Therefore, the area of one face = a2 [By area of square formula]
E. If the edge of the cube measures 4 centimetres, what is the area of one face of the cube?
Answer:
According to the above information:
Let the length of an edge of a cube is a.
Therefore, the area of one face = a2 [By area of square formula]
a = 4
4 x 4 = 16 square.cms
F. What is the total area of all 6 faces of the cube?
Answer:
There are total 6 faces. Therefore,
TSA of cube = a2 + a2 + a2 + a2 + a2 +a2
TSA of cube = 6a2
A cube consists of an ‘n’ number of square units. Hence the space covered by these square units on the surface of the cube is the surface area. Basically, the surface area is the sum of all the areas of all the shapes that cover the surface of the shape or object. In the case of a cube, there are 6 faces. So the surface area will be the sum of all the area of six faces.
We know that one face of the cube is 16 square.cms
According to the formula:
The total area of all 6 faces of the cube = 16(6) = 96 square cms
Turn and Talk What do all six faces of the cube have in common? Is there another way to calculate the total area of the faces?
Answer:
All six faces of the cube have the same shape and the same area.
Another way to calculate the total area of the faces is to add the 16 for 6 times.
16 + 16 + 16 + 16 + 16 + 16
Connect to Vocabulary
Surface area is the sum of the areas of the faces, or surfaces, of a three-dimensional figure.
A pyramid is a three-dimensional figure with a polygon base and triangular sides that all meet at a common vertex.
Question 2.
Look at the square pyramid shown. How many faces does the pyramid have? Explain how you know.
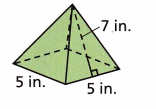
Answer:
A square pyramid is a three-dimensional geometric shape that has a square base and four triangular sides that are joined at a vertex. It is a polyhedron (pentahedron) with five faces. A square pyramid consists of a square base and four triangles connected to a vertex. Its base is a square and the side faces are triangles with a common vertex.
5 faces, 4 triangles, 1 square.
A. Fill in the boxes of the net for the square pyramid shown with the correct dimensions.
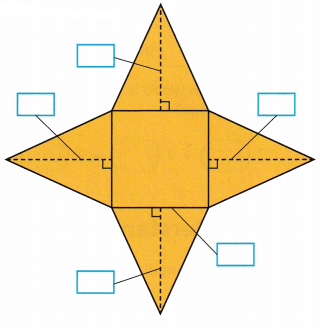
Answer:
According to the above-given diagram (question 2)
we can fill the given diagram in part A.
And we already know that 5 faces, 4 triangles, 1 square.
height is 7 and the base is 5
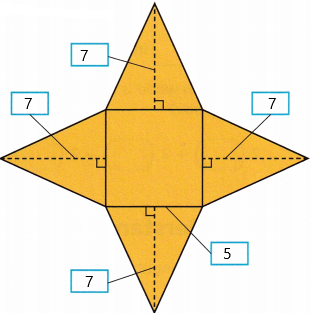
B. What formula can you use to find the area of one triangular face?
Answer:
The formula we can use is:
Area = bh/2
area = 7(5)/2
area = 35/2
C. What is the area of one triangular face?
Answer:
According to the above formula, we can find out the area of one triangular face.
Area = bh/2
area = 7(5)/2
area = 35/2
area = 17.5 square inches.
D. What is the area of the square base?
Answer:
The base of a square pyramid is square-shaped. Thus, the base area of the square pyramid can be calculated using the formula, Base Area of Pyramid = a^2, where, a is the length of the base of square pyramid.
we know that the square base is 5.
area = 5 . 5
area =25 square inches.
E. How can you find the surface area of the square pyramid?
Answer:
Surface Area of a square pyramid = Area of the base + Area of 4 triangles
Then, the formula to calculate the surface area is:
Surface Area = s2 + 2sl square units.
According to the above information (part D and part C). We substituted the values in the formula.
Surface area = 25 + (17.5)4
Surface area = 25 + 75
Syrface area = 95 square inches.
F. What is the surface area of the square pyramid?
Answer:
According to the above information (part E)
Therefore, the answer for the surface area of the square pyramid is 95 square inches.
Turn and Talk Is there another way to solve for the surface area? Explain.
Answer:
– To find the surface area, work out the area of each face and add them together.
– Well you can also multiply the perimeter by the length of the edge, then divide by the length of the face.
Question 3.
Chandra is making a jewellery box and needs to know how much wood to buy.

A. Use the dimensions shown to label the side lengths of each face of the net.
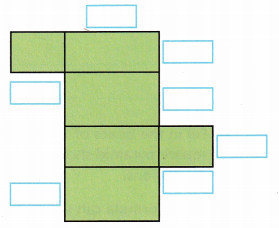
Answer:
The length is 7
according to that, we filled the diagram.
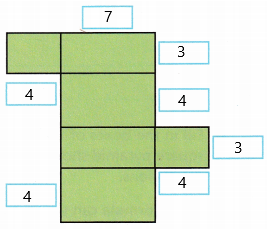
B. Find the area of its right and left faces.
![]() in. ×
in. × ![]() in. =
in. = ![]() in2
in2
Answer:
In the below diagram, the right and left faces are shown.

4 x 3 = 12 square inches.
C. Find the area of its top and bottom faces.
![]() in. ×
in. × ![]() in. =
in. = ![]() in2
in2
Answer:
In the below diagram, the top and bottom faces are shown.

7 x 4 = 28 square inches
D. Find the area of its front and back faces.
![]() in. ×
in. × ![]() in. =
in. = ![]() in2
in2
Answer:
In the below diagram, the front and back faces are shown.

7 x 3 = 21 square inches
E. How much wood !s needed to make the jewelry box?
2 (![]() ) + 2 (
) + 2 (![]() ) + 2(
) + 2(![]() ) =
) = ![]() square inches
square inches
Answer:
= 2(12) + 2(28) + 2(21)
= 24 + 56 + 42
= 122 square inches.
Check Understanding
Question 1.
Look at the triangular prism shown.
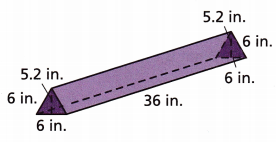
A. This prism has _________ triangular faces and __________ rectangular faces.
Answer:
The prism has 2 triangular faces and 3 rectangular faces.
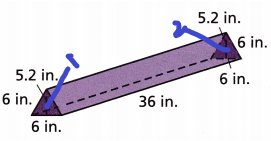
B. Draw a net to represent the prism.
Answer:
In a net, we can see all five faces individually. Remember, a net is a two-dimensional composite shape which consists of two triangles and three rectangles.

C. Find the surface area of the triangular prism.
2[\(\frac{1}{2}\)(![]() ) (
) (![]() )] + 3[
)] + 3[![]() •
• ![]() ] =
] = ![]() in2
in2
Answer:
= 2[1/2(5.2)(6)] + 3[36 . 6]
= 31.2 + 3(216)
= 31.2 + 648
= 679.2
Therefore, the surface area of the triangular prism is 679.2 square inches.
On Your Own
Question 2.
Keisha is helping her sister build triangular pyramids as containers to package her bracelets.

A. Draw and label a net that Keisha can use to fold and make the container.
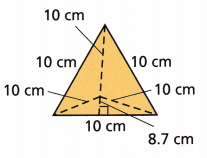
Answer:
Nets are useful to find the surface area of solids. A triangular pyramid net is a pattern that forms when its surface is laid flat, showing each triangular face in the two-dimensional (2D) form. The triangular pyramid net consists of four triangles.
The net is to store bracelets:
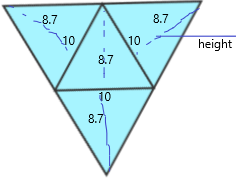
B. How much cardboard do they need for each container?
Answer:
The surface area of a triangular pyramid = bh/2
There should be 4 triangles so the formula is:
surface area = 4(bh/2)
surface area = 4(10 x 8.7)/2
surface area = 4(87)/2
surface area = 348/2
surface area = 174 square cms.
Question 3.
Reason Can the following nets be folded into cubes? If not, explain.
A.
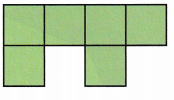
Answer:
The above-given net cannot be folded into cubes because there are 2 bottoms
B.
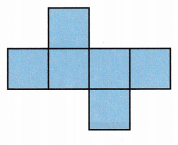
Answer:
The geometric nets of a cube are formed when we extend a cube. In general, a geometric net can be defined as a two-dimensional figure that can be modified to form a three-dimensional figure. This means that when we fold a geometric net of a cube, we will form a cube.
For a geometric net to form a three-dimensional solid, it must meet the following conditions:
– The geometric net and the 3D figure must have the same number of faces. This means that the geometric net of a cube must have 6 faces.
– The shapes of the faces in the geometric net must be the same as the shapes of the faces in the 3D shapes. This means that a geometric net of a cube has square faces.
Therefore, we conclude that the geometric net of a cube must have 6 square faces. Also, the faces need to be located in specific positions so that when folding them, we form a cube.
According to the above conditions:
The above-given net can be folded into a cube.
C.
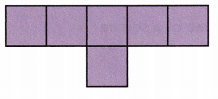
Answer:
The above-given net cannot form a cube because it overlaps.
For Problems 4-7, identify what solid figure the net folds into. Then find the surface area of the net.
Question 4.
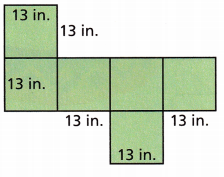
Answer:
The above-given net is a cube because it satisfies the following conditions:
For a geometric net to form a three-dimensional solid, it must meet the following conditions:
– The geometric net and the 3D figure must have the same number of faces. This means that the geometric net of a cube must have 6 faces.
– The shapes of the faces in the geometric net must be the same as the shapes of the faces in the 3D shapes. This means that a geometric net of a cube has square faces.
Therefore, we conclude that the geometric net of a cube must have 6 square faces. Also, the faces need to be located in specific positions so that when folding them, we form a cube.
we already know that,
the surface area of the cube = 6. s^2
surface area = 6(13 x 13)
surface area = 6(169)
surface area = 1014 square inches
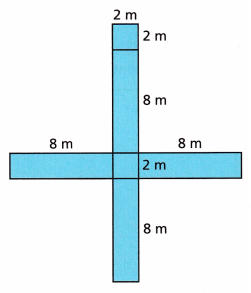
Question 5.
Answer:
It is a rectangular prism.
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– the surface area of the rectangular prism = 2(lw + wh + hl)
surface area = 2(2×2 + 2×8 + 2×8)
surface area = 2(4 + 16 + 16)
surface area = 2(36)
surface area = 72 square metres.
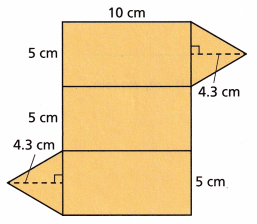
Question 6.
Answer:
It is a triangular prism.
surface area = bh/2
surface area = 5 x 4.3/2
surface area = 21.5/2
surface area of one triangle= 10.75
surface area of two triangles=10.75 x 2 = 21.5
There are three rectangles:
surface area of rectangle = length x width
surface area of one rectangle = 10 x 5 = 50
surface area of three rectangles = 50 x 3 = 150
Now add both the values:
The total surface area of a rectangular prism = 21.5 + 150 = 171.5 square cms.
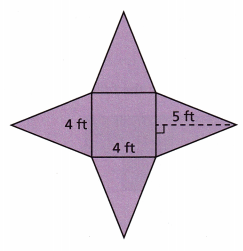
Question 7.
Answer:
It is a square pyramid.
– A square pyramid is a three-dimensional geometric shape that has a square base and four triangular bases that are joined at a vertex. It is a polyhedron (pentahedron) with five faces. A square pyramid consists of a square base and four triangles connected to a vertex. Its base is a square and the side faces are triangles with a common vertex.
the surface area of the square = side^2
surface area of square = 4 x 4 = 16 square ft.
The surface area of the triangle = bh/2
surface area of triangle = 4 x 5/2 = 20/2 =10
There are four triangles so the surface area = 4 x 10 = 40 square ft.
Now add both the values:
The total surface area of the square pyramid = 16 + 40 = 56 square ft.
I’m in a Learning Mindset!
How did I apply prior knowledge to find the surface area of a square pyramid in Task 2?
Answer:
Lesson 13.1 More Practice/Homework
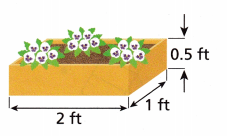
Question 1.
Reason George is building flower boxes to sell as gifts. Draw and label a net to represent a flower box. Then find the amount of material George needs for each box. Explain why you drew the net the way you did.
Answer:
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– the surface area of the rectangular prism = 2(lw + wh + hl)
surface area = 2(2×1 + 1×0.5 + 0.5×2)
surface area = 2(2 + 0.5 + 1)
surface area = 2(3.5)
surface area = 7 square ft.
Question 2.
Math on the Spot Finds the surface area of the prism.
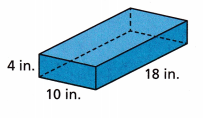
Answer:
The surface area of a prism refers to the amount of total space occupied by the flat faces of the prism. Finding the surface area of a prism means calculating the total space occupied by all the faces of that respective type of prism or the sum of the areas of all faces (or surfaces) in a 3D plane.
The Surface Area of a Prism Formula is given as,
The surface Area Of A Rectangular Prism is A = 2 (wl + lh + hw)
Surface area = 2 (18 x 10 + 10 x 4 + 4 x 18)
Surface area = 2 (180 + 40 + 72)
Surface area = 2 ( 292)
Surface area = 584 square inches
For Problems 3-4, identify what solid figure the net folds into. Then find the surface area of the figure.
Question 3.
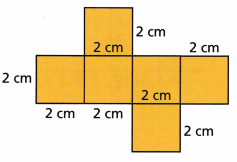
Answer:
The above-given net is a cube because it satisfies the following conditions:
For a geometric net to form a three-dimensional solid, it must meet the following conditions:
– The geometric net and the 3D figure must have the same number of faces. This means that the geometric net of a cube must have 6 faces.
– The shapes of the faces in the geometric net must be the same as the shapes of the faces in the 3D shapes. This means that a geometric net of a cube has square faces.
Therefore, we conclude that the geometric net of a cube must have 6 square faces. Also, the faces need to be located in specific positions so that when folding them, we form a cube.
we already know that,
the surface area of the cube = 6. s^2
surface area = 6(2 x 2)
surface area = 6(4)
surface area = 64 square cms
Question 4.
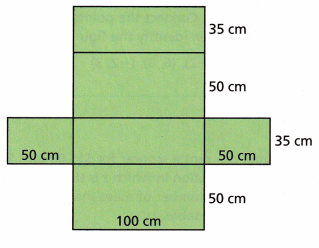
Answer:
It is a rectangular prism.
– A rectangular prism has 6 faces, 12 edges and 8 vertices
– The top and base of the rectangular prism are always a rectangle
– the surface area of the rectangular prism = 2(lw + wh + hl)
surface area = 2(100×50 + 50×35 + 35×100)
surface area = 2(5000 + 1750 + 3500)
surface area = 2(10250)
surface area = 20500 square centimetres.
Test Prep
Question 5.
Match the net to its three-dimensional figure.
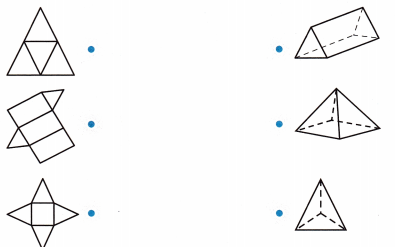
Answer:
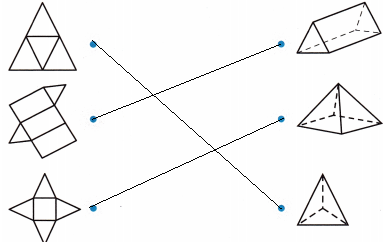
Question 6.
Assume that the box has no top. What is the surface area of the box shown?
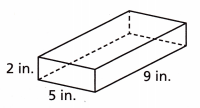
(A) 64 in2
(B) 73 in2
(C) 90 in2
(D) 101 in2
Answer: Option C is correct.
Surface area of the box = l x b x h
Surface area = 5 x 9 x 2
Surface area = 90 square.inches.
Spiral Review
Question 7.
Jem is carpeting a room. A drawing of the floor is shown. How much carpet will she use?
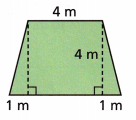
Answer:
The area of a trapezium can be found by taking the average of the two bases of a trapezium and multiplying it by its altitude. So, the area of the trapezium formula is given as:
Here we need to find out the area:
area of trapezium = (a + b)/2 x h
area of trapezium = (4 + 6)/2 x 4
area = 10/2 x 4
area = 5 x 4
area of trapezium = 20 square. metre
Question 8.
The vertices of a polygon are given. Graph the ordered pairs. Connect the points in the order they are given. Then identify the figure.
(-4, -2), (4, -2), (6, 3), (-2, 3)
Answer:
The coordinates are connected in the graph below:
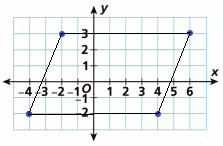
The polygon we got was a parallelogram.
A parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are equal in length, and the opposite angles are equal in measure. Also, the interior angles on the same side of the transversal are supplementary. The Sum of all the interior angles equals 360 degrees.
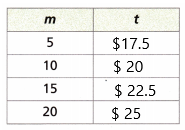
Question 9.
Brianna can rent a scooter for $15.00 plus $0.50 per mile. Write an equation in which t is the cost to rent a scooter and m is the number of miles she rode the scooter. Complete the table.
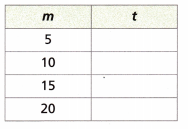
Answer:
The cost of a scooter which can be given as rent by Brianna = $15
The cost per mile = $0.50
We need to write the equations for the given number of miles.
The number of miles given = 5
The cost to rent a scooter for 5 miles = 5 x 0.50 + 15
The cost to rent a scooter for 5 miles= 2.5 + 15 = $17.5
The number of miles given = 10
The cost to rent a scooter for 5 miles = 10 x 0.50 + 15
The cost to rent a scooter for 5 miles= 5 + 15 = $20
The number of miles given = 15
The cost to rent a scooter for 5 miles = 15 x 0.50 + 15
The cost to rent a scooter for 5 miles= 7.5 + 15 = $22.5
The number of miles given = 20
The cost to rent a scooter for 5 miles = 20 x 0.50 + 15
The cost to rent a scooter for 5 miles= 10 + 15 = $25