Into Math Grade 6 Module 12 Lesson 4 Answer Key Find Area of Composite Figures

We included HMH Into Math Grade 6 Answer Key PDF Module 12 Lesson 4 Find Area of Composite Figures to make students experts in learning maths.

HMH Into Math Grade 6 Module 12 Lesson 4 Answer Key Find Area of Composite Figures

I Can find the area of any composite figure.

Step It Out

You can find the area of composite figures by breaking them into familiar figures such as triangles or quadrilaterals.
Connect to Vocabulary A composite figure is a figure made up of simple geometric shapes.

Question 1.
The figure shown gives the dimensions of a city park. What is the area of the city park?

A. What different shapes could the figure be divided into?
Answer:
Rectangle, trapezium.

Explanation:
The figure can be divided into different shapes Rectangle and trapezium.

B. There are several ways to divide the figure. The figure is divided into two quadrilaterals with a horizontal line. What are the two quadrilaterals?

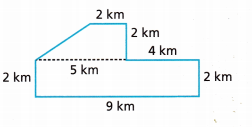
Answer:

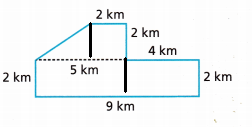
C. Find the area of the top shape.

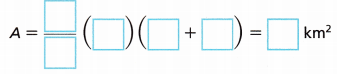
Answer:
The area of the trapezium is 4 km²

Explanation:
Given,
The given figure is a trapezium
The area of the trapezium is A = \(\frac{1}{2}\) × ( a + b) × h
a = 2 km b = 2 km and h = 2 km
A = \(\frac{1}{2}\) × 2 × (2 + 2)
A = 4 km²

D. Find the area of the bottom shape.
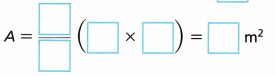
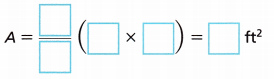
A = × = km²
Answer:
Given,
The figure is rectangle
l = 9 km and b = 2 km
Area of the rectangle is l × b
Area = 2 × 9
Area = 18 km² .

E. Total area = Area of top shape + Area of bottom shape
= km² + km²
= km²
The area of the park is ___________ square kilometers.
Answer:
22 km².

Explanation:
Area of the top shape = 4 km²
The area of the bottom shape is 18 km².
Total area = Area of top shape + Area of the bottom shape
Total area = 18 km² + 4 km²
Area = 22 km²

Turn and Talk In what other ways could you divide the figure? Explain.
Answer:
We can divide the figure in one triangle, square and one rectangle.

Question 2.
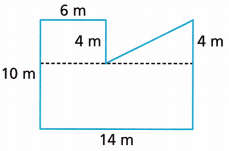
The roof of a building is shown. What is its area?

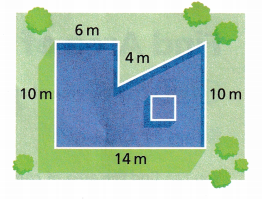
A. What different shapes could the roof be divided into?
Answer:
The roof can be divided into a square and a 0right-angled triangle.

B. The figure represents the roof. The figure is divided with a horizontal segment.
The top shapes are a ____________ and a _________. The bottom shape is a _____________.

Answer:
Rectangle and right-angle triangle.

Explanation:
The top shape is a rectangle and right-angle triangles.

C. Find the area of the right triangle. The base is 8 meters because
The base is 8 meters because m – m = 8 meters.

Answer:
Area of the triangle is 16 m².

Explanation:
Given base =  8 m and height = 4 m
area of the triangle is \(\frac{1}{2}\) × b × h
area = \(\frac{1}{2}\) × 8 × 4
area = 16 m².

D. Find the area of the top rectangle.
A = m × m = m²
Answer:
Area of the top rectangle is 24 m².

Explanation:
Given,
l = 4 m and breadth = 6 m
Area of the top rectangle is l × b
Area = 4 × 6
Area = 24 m².

E. Find the area of the bottom rectangle.
The width is 6 meters because m – m = 6 meters.
A = m × m = m²
Answer:
The area of the bottom rectangle is 56 m².

Explanation:
Given,
length = 14 m and width = 6 m = 10 m – 4 m
Area of the bottom rectangle is 14 × 4
Area = 56 m².

F. Total area = Area of triangle + Area of top rectangle + Area of bottom rectangle
= m² + ² + m² = m²
Answer:
Area = 96 m²

Explanation:
Area of the triangle is 16 m².
Area of the top rectangle is 24 m².
The area of the bottom rectangle is 56 m².
Total area = Area of triangle + Area of top rectangle + Area of bottom rectangle
Area = 16 + 24 +56
Area = 96 m²

G. The area of the roof is ____________ square meters.
Answer:
Area of the roof is 140 m²

Explanation:
Given,
length = 14 m and width = 10m
Area of the roof is = l × b
Area = 14 × 10
Area = 140 m²

H. How else could you divide the figure to find the area?
Answer:

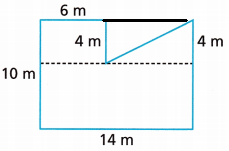
Turn and Talk How could you find the area of the figure using subtraction? What figures would you use? Explain.
Answer:

Question 3.
Paula is painting the side of a house and needs to know how much paint to buy. Each gallon of paint will cover a certain number of square feet. What is the area, in square feet, of the side of the house?
A. The side of the house is divided into two shapes. The top shape is a ___________, and the bottom shape is a ____________.

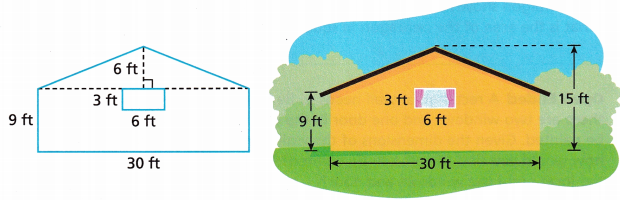
Answer:
342 ft²

Explanation:
9 × 30 + 30 × (15 -9) × \(\frac{1}{2}\) – (3 × 6)
270 + 90 -18
342 ft²

B. Find the area of the rectangle.
A = ft × ft = ft²
Answer:
Area of the rectangle is 270 ft²

Explanation:
Given,
Length = 30 ft and width = 9 ft
Area of the rectangle = 30 × 9
Area = 270 ft²

C. Find the area of the triangle.
The triangle has a height of 6 feet because 15 – = 6.

Answer:
The triangle has a height of 6 feet because 15 – 9 = 6.
base = 3 ft
Area of the traingle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 3 × 6
Area = 9 ft²

D. Find the area of the rectangular window.
A = ft × ft = ft²
Answer:
Area of the rectangular window = 18 ft².

Explanation:
Given,
Length = 6 ft and width = 3 ft
Area of the rectangle is l × b
Area = 6 × 3
Area = 18 ft².

E. Total area = Area of rectangle + Area of triangle – Area of window
= ft² + ft² – ft² = ft²
Answer:
Total area = 297 ft²

Explanation:
Given,
area of a rectangle is 270 ft²
area of triangle is  9 ft²
The area of window is 18 ft²
Therefore total area = Area of rectangle + Area of a triangle – Area of window
Total area = 270 + 9 +18
Total area = 297 ft²

Check Understanding

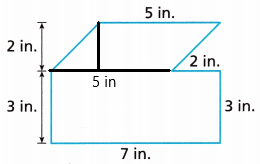
Question 1.
Find the area of the figure shown.

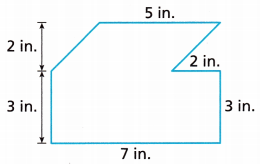
Answer:

Question 2.
What is the area of the picture frame in square inches? Show how you solved the problem.

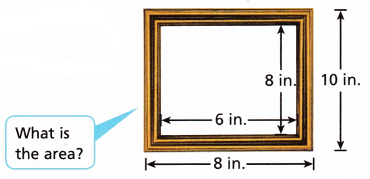
Answer:
Area of the box is 80 + 48 = 128 square inches

Explanation:
Given,
The length of the bigger box is 10 in
width is 8 in
The area of the bigger box is 10 × 8 = 80 square inches
length of the smaller box is 8 in and the width is 6 in
Area if the smaller box is 8 × 6 = 48 square inches
Total area of the box is 80 + 48 = 128 square inches.

On Your Own

Question 3.
The outline of Sara’s family room, including the entry, is shown. Sara wants to carpet the family room. How many square feet of carpet does she need?

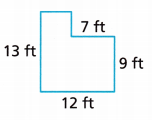
Answer:
128 ft²

Explanation:
S = 12 × 13 – 7 × (13 – 9)
S = 156 – (7 × 4)
S = 156 – (28)
S = 128 ft²

Question 4.
The pentagon shown is divided into four triangles and a rectangle. What is the area of the pentagon in square centimeters?

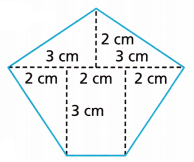
Answer:

Question 5.
Open-Ended A rectangular wall needs to be painted, but there are two windows and one door in the wall that will not be painted. Given the dimensions of the wall, windows, and door, how would you find the area to be painted? Do you need to know the location of the windows and door?
Answer:

Question 6.
Geography The state of Utah is shown. All the angles measure 90°. What is the area, in square miles, of the state?

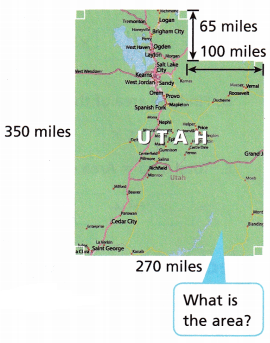
A. Find the area of the larger rectangle that contains the state. Show the equation you used.
_________ square miles
Answer:
94,500 miles.

Explanation:
350 × 270 miles = 94,500 miles

B. Find the area of the rectangle that is missing from the top-right corner of the larger rectangle. Show the equation you used.
__________ square miles
Answer:
65 miles × 100 miles = 6500 square miles.

C. Area of the state of Utah ≈ ___________ square miles
Answer:
94,500 square miles – 6500 = 88,000 Square miles.
The area of the rectangle is equal to the width times length.

For Problems 7-8. find the area.

Question 7.

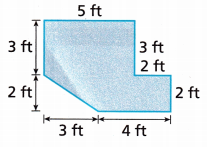
Answer:
The area of the figure is 32 ft²

Explanation:

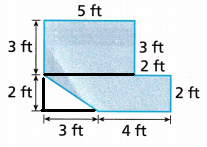
Given,
The figure has one rectangle, one triangle, and another rectangle.
Let us calculate the area of the first rectangle l × b
l = 3 ft and width = 5 ft
Area = 3 × 5
Area = 15 ft²
Next, find the area of the triangle
Area of the traingle is \(\frac{1}{2}\) × b ×h
h = 2 ft and b = 3 ft
Area = \(\frac{1}{2}\) × 2 × 3
Area = 3 ft²
Area of the second rectangle is l × b
l = 2 ft and width = 7 ft
Area = 2 × 7
Area = 14 ft²
The total area of the given figure = area of the first rectangle + Area of the triangle + Area of the second rectangle
Total area = 15 ft² + 3 ft² +  14 ft²
Total area = 32 ft²

Question 8.

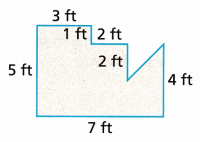
Answer:
Total area = 31 ft²

Explanation:

The given figure contains one rectangle, Two squares, and one smaller triangle.
Let us calculate the area of the square is s × s
Given the side of the square is 3 ft
The area of the square is 3 × 3
Area = 9 ft²
Calculate the area of the other square
Area = s × s
The side of the square is 2 ft.
Area = 2 × 2 = 4 ft²
Next, calculate the area of the rectangle = l × l
L = 2 ft and width = 7 ft
The area of the rectangle is 2 × 7
Area = 14 ft²
Last, calculate the area of the triangle.
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 2 × 4
Area of the triangle is 4 ft²
Total area of the figure is = 9 + 4 + 14 + 4
Total area = 31 ft²

Question 9.
My Construct Arguments The two figures shown have the same area. Without calculating the area, explain why this is so.

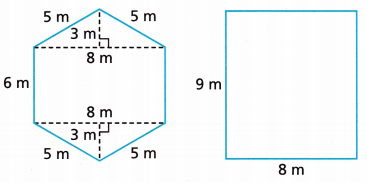
Answer:

Question 10.
In the compass rose shown, each triangle has the same area, and the center is a square. What is the area of the figure in square inches?

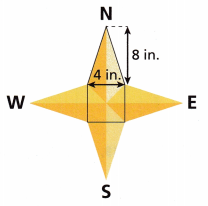
Answer:
80 sq inches.

Explanation:
Given,
S = 4 × 8 × \(\frac{1}{2}\) × 4 + (4 × 4)
S = 64 + 16
S = 80 sq inches.

Question 11.
Sandy has built a triangular pool and wants to add a rectangular deck around it as shown in the figure. How many square feet of wood does Sandy need for the deck?

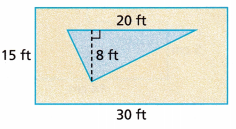
Answer:
Area = 530 sqaure feet

Explanation:
Given,
base = 20 ft and height = 8 ft
The area of the triangular pool is \(\frac{1}{2}\) × 20 × 8
Area = 10 × 8
Area = 80 square ft
Area of the rectangle is 15 × 30 = 450 sq ft
Total area = 450 + 80 = 530 square ft.

For Problems 12-13, find the area of the figure.

Question 12.

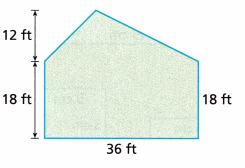
Answer:
Area of the total figure = 216 + 648 = 864 sq ft

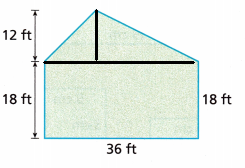
The given figure has one rectangle and one triangle
l = 18 ft and w = 36 ft
Area of the rectangle = 18 × 36
Area = 648 sq ft
Area of the traingle = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 36 × 12
Area = 18 × 12
= 216 sq ft
Total area = 216 + 648 = 816 sq ft

Question 13.

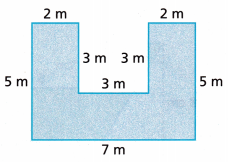
Answer:
The area of the given figure is 26 sq cm.
Explanation:

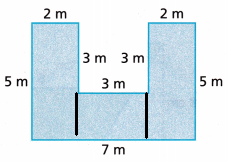
The given figure has three rectangles
Let us find the area of the rectangles given
The area of the first rectangle is 5 × 2 = 10 sq cm
The area of the second rectangle is 5 × 2 = 10 sq cm
The area of the third rectangle is 3 × 2 = 6 sq cm
Total area of the figure = 10 + 10 + 6 = 26 sq cm

Question 14.
Reason Piazza San Marco ¡s a famous open plaza in Venice, Italy. Its shape is shown. How would you find the approximate area of the plaza?

Answer:

Question 15.
Open-Ended Draw a composite figure with at least one slanted side and an area of 24 square units.

Answer:

For Problems 16-19. find the area of the figure.

Question 16.

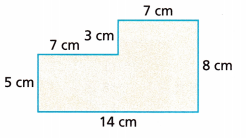
Answer:

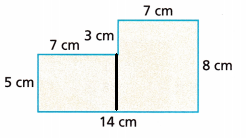
In the given figure there are two rectangles
Area of one rectangle = l × b
Length = 5 cm
width = 7 cm
Area = 5 × 7
Area = 35 cm²
Area of another rectangle is l × b
l = 8 cm and b = 7cm
Area of second rectangle is 8 × 7 = 56 cm²
Therefore total area of the figure is 35 + 56 = 91 cm²

Question 17.

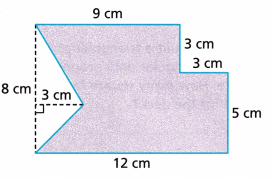
Answer:
Area of the figure = 99 square cm.

Explanation:

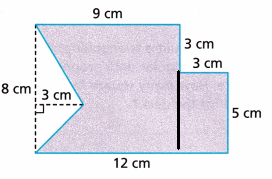
The given figure has two rectangles and one triangle
Let us find the area of the first rectangle
Given l = 8 cm and width = 9 cm
Area = 8 × 9 = 72 square cm
Next, find the area of the other rectangle
l = 5 cm and width = 3 cm
Area = 5 × 3 = 15 square cm
Now find the area of the triangle
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 8 × 3
Area = 4 × 3
= 12 square cm
Total area of the figure is 72 + 15 + 12 = 99 square cm.

Question 18.

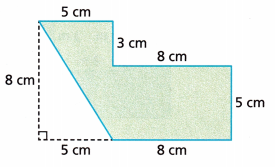
Answer:

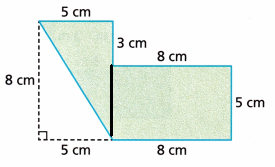
Area of the figure is 40 + 40 + 20 = 100 square cm.

Explanation:
The given figure has two rectangles and one triangle
First, calculate the area of the first rectangle
l = 8 cm and width = 5 cm
Area = 8 × 5 = 40 square cm
Next, calculate the area of another rectangle
l = 8 cm and width = 5 cm
Area = 8 × g = 40 square cm
Last calculate the area of the triangle = \(\frac{1}{2}\) × b × h
base = 5 cm and height = 8cm
Area = \(\frac{1}{2}\) × 5 × 8
Area = 20 square cm
The total area of the figure is 40 + 40 + 20 = 100 square cm.

Question 19.

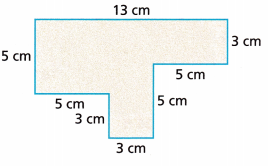
Answer:
Area of the square = 55 square cm.

Explanation:
Given,
The given figure has one square, two rectangles
Let us find the area of the square
side of the square is 5 cm
Area = 5 × 5 = 25 square cm.
Now let us calculate the area of the rectangle
Area  = 3 × 5 = 15 square cm
Another rectangle area is 3 × 5 = 15 square cm
The total area of the figure is 25 + 15 + 15 = 55 square cm.

Lesson 12.4 More Practice/Homework

Question 1.
The floor plan for a house is shown. Vertical lengths and horizontal lengths are given. What is the floor area in square feet?

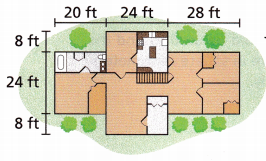
Answer:
Area = 2880 ft²

Explanation:
Given,
Length = 8 + 24 + 8 = 40 ft
width = 20 + 24 + 28 = 72 ft
Area of the given figure is length × width
Area = 40 × 72
Area = 2880 ft²

Question 2.
On a baseball field, home plate is where the batter stands to hit and where a runner scores a run What is the area of the home plate diagram shown in square inches?

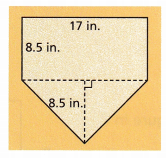
Answer:
Area of the home plate diagram shown in square inches is 180.6 in²

Explanation:
17 × 8.5 + \(\frac{1}{2}\) × 8.5 × 8.5
17 × 8.5 + 36.1
144.5 + 36.1
180.6 in²

Question 3.
Math on the Spot Kirsten wants to buy wooden flooring for her bedroom. The diagram shows the bedroom’s shape and dimensions. One case of flooring will cover 25 square feet. How many cases of flooring will Kirsten need to buy? Explain.

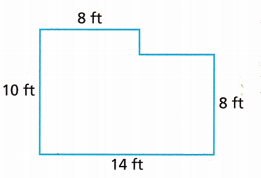
Answer:
Kirsten needs to buy 2 cases of flooring.
A = 8 × 10 + 8 × 14
A = 8 × 14 + 2 × 8

Question 4.
Attend to Precision Robert is designing hexagonal tiles that are made up of 12 identical right triangles, as shown. Write three equations Robert can use to find the area A of the hexagonal tile in square centimeters.

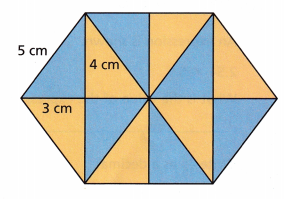
Answer:
194.85 cm²

Explanation:
Area = \(\frac{3 √3}{2}\)  × a²
Area = \(\frac{3 √3}{2}\) × 5 × 5 + \(\frac{3 √3}{2}\) × 5 × 5 + \(\frac{3 √3}{2}\) × 5 × 5

Test Prep

Question 5.
A figure is shown.
Which equations could be used to find the area A of the figure in square centimeters? Select all that apply.

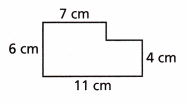
(A) A = 6 × 11
(B) A = 7 × 6 + 4 × 4
(C) A = 4 × 11 + 2 × 7
(D) A = 7 × 6 + 4 × 11
(E) A = 6 × 11 – 4 × 2
Answer:
A = 7 × 6 + 4 × 4
A = 4 × 11 + 2 × 7

Explanation:
The equations could be used to find the area A of the figure in square centimeters are A = 7 × 6 + 4 × 4, A = 4 × 11 + 2 × 7.

Question 6.
A figure is shown.
What is the area of the figure in square meters?

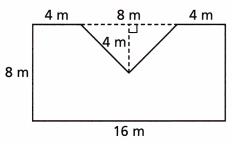
Answer:
The area of the figure is 144 m².

Explanation:
Given,
The figure has one rectangle and triangle.
First calculate the area of the rectangle = l × b
l = 8 m and width = 16 m
Area = 16 × 8
Area = 128 m².
Area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 4 × 4
Area = 8 m².
The total area of the figure = Area of the rectangle + Area of one right angle triangle + Area of the second right angle
Area = 128 + 8 + 8
Area = 144 m².

Question 7.
A figure is shown.
Write an equation to find the area A of the figure in square feet.

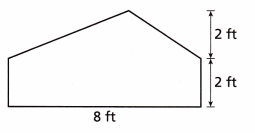
Answer:
Given, one side is 8 ft and other side is 2ft + 2ft = 4ft
We need to calculate the area of the given figure
By the given dimensions we can tell that the figure is a rectangle
The area of the rectangle is l × b
Area = 8 × 4
Area = 32 square feet.

Spiral Review

Question 8.
An expression is shown.
2.54 × 5.5
What is the value of the expression?
Answer:
13.97

Explanation:
The value of the expression for 2.54 × 5.5 is 13.97.

Question 9.
Write \(\frac{12}{15}\) as a decimal.
Answer:
0.8

Explanation:
The decimal number for \(\frac{12}{15}\) is 0.8