Into Math Grade 6 Module 12 Lesson 3 Answer Key Develop and Use the Formula for Area of Trapezoids

We included HMH Into Math Grade 6 Answer Key PDF Module 12 Lesson 3 Develop and Use the Formula for Area of Trapezoids to make students experts in learning maths.

HMH Into Math Grade 6 Module 12 Lesson 3 Answer Key Develop and Use the Formula for Area of Trapezoids

I Can use the area formula for a trapezoid given the lengths of its bases and its height.

Spark Your Learning

Quinn is putting sod in a yard, but is leaving part of the area without grass for a patio. He needs to know how many square feet of sod to buy. The shaded area shown is the part of the yard that will have grass. How many square feet of sod does Quinn need?

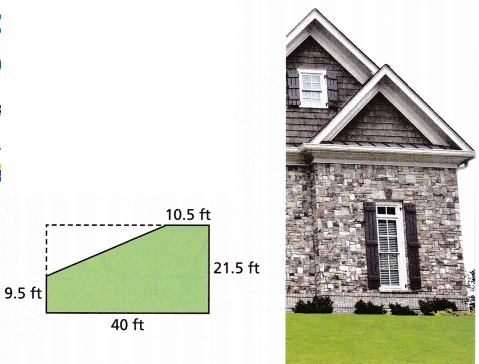
Answer:

Turn and Talk How does knowing the formulas for the areas of rectangles and triangles help in finding the areas of other figures?
Answer:

Build Understanding

Trapezoids have two bases. Any pair of parallel sides of a trapezoid can be the bases of the trapezoid. The height of a trapezoid is the perpendicular distance from the base to the opposite vertex or side.
Conned to Vocabulary
A trapezoid is a quadrilateral with at least one pair of parallel sides.

Question 1.
How can you find the area of a trapezoid?
A. Notice that two copies of the same trapezoid fit together to form a parallelogram. How does the area of the trapezoids compare to the area of the parallelogram?

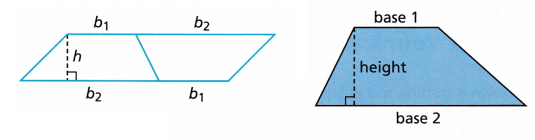
Answer:
The height of the parallelogram is equal to the height of the trapezoid, but the base is the sum of the two bases of the trapezoid. Therefore the area of parallelograms is height × (base1 + base2).

B. How does the height of the trapezoid compare to the height of the parallelogram in Part A?
Answer:
The height of the parallelogram is equal to \(\frac{1}{2}\) the height of the trapezoid.

C. How can you find the length of the base of the parallelogram in Part A?
The length of the base of the parallelogram is the of the ___________ of the trapezoid.
Answer:
Area of parallelogram = ((b1+b2) + (b1 +b2)) × h

Explanation:
The length of the base of the parallelogram is the of the half of the trapezoid.

D. How can you use the area formula for a parallelogram to write an area formula for a trapezoid?
Area of parallelogram = bh

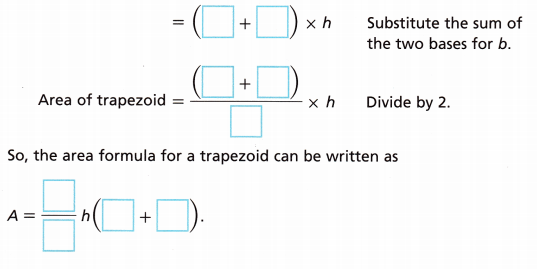
Answer:

Turn and Talk Will this area formula work for all trapezoids regardless of size? Explain.
Answer:

Step It Out

Question 2.
What is the area of the trapezoidal cactus garden shown?

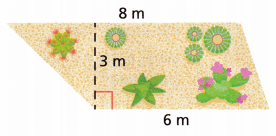
A. What is the formula for the area of a trapezoid?
Answer:
Area = 21 m²

Explanation:
Given, b1 = 6m, b2 = 8m and height = 3m
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{6 + 8}{2}\) × 3
Area = \(\frac{14}{2}\) × 3
Area = 7 × 3
Area = 21 m²

B. What are the dimensions of the trapezoid?
b₁ = m
b₂ = m
h = m
Answer:
b₁ = 6m, b₂ = 8m and h = 3m

Explanation:
The dimensions of the trapezoid is b₁ = 6m, b₂ = 8m and h = 3m

C. Substitute the values for b₁, b₂, and h into the formula.
A = \(\frac{1}{2}\)() ( + )
Answer:
A = \(\frac{1}{2}\) 3 × (6+8)

D. Add inside the parentheses.
A = \(\frac{1}{2}\)() ()
Answer:
A = \(\frac{1}{2}\) 3 × (6+8)
A = \(\frac{1}{2}\) 3 × (14)

E. Multiply.
A = \(\frac{1}{2}\) ()
Answer:
A = \(\frac{1}{2}\) 42.

F. Divide.
A = square meters
Answer:
A = 21 square meters

G. The area of the cactus garden is ____________ square meters.
Answer:
The area of the cactus garden is 21 square meters

Question 6.
What is the area of the trapezoid shown? Remember, the bases are the two parallel sides.

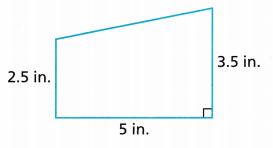
A. What is the formula for the area of a trapezoid?
Answer:
Given, b₁ = 2.5 in , b₂ = 3.5 in and height = 5 in
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{2.5 + 3.5}{2}\) × 5
Area = \(\frac{6}{2}\) × 5
Area = 3 × 5
Area = 15 square inches.

B. What are the dimensions of the trapezoid? ‚
b₁ = in.
b₂ = in.
h = in.
Answer:
b₁ = 2.5 in, b₂ = 3.5 in and height = 5 in.

Explanation:
The dimensions of the trapezoid are b₁ = 2.5 in, b₂ = 3.5 in and height = 5 in.

C. Substitute the values for b₁, b₂, and h into the formula.
A = \(\frac{1}{2}\) ()( + )
Answer:
A = \(\frac{1}{2}\) × 5 × (2.5 + 3.5)

D. Simplify.
A = square inches
Answer:
A = \(\frac{1}{2}\) × 5 × (2.5 + 3.5)
A = \(\frac{1}{2}\) × 5 × (6)
A = \(\frac{30}{2}\)
A = 15 square inches.

E. The trapezoid has an area of ___________ square inches.
Answer:
Area = 15 square inches.

Explanation:
The trapezoid has an area of 15 square inches.

Turn and Talk Could you find the area of a trapezoid using triangles? Explain.
Answer:
The triangle has the base (a + b) and height h. By applying the area of a triangle formula, then the area of the trapezoid or triangle is \(\frac{1}{2}\) × b × h

Question 4.
A teacher has a table in the shape of the trapezoid shown. What is the height of the tabletop in feet?

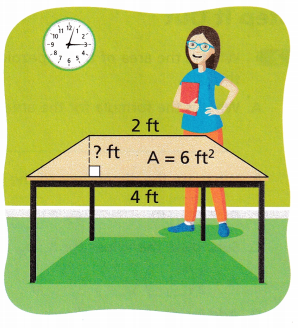
A. What is the formula for the area of a trapezoid?
Answer:
h = 2 ft

Explanation:
Given,
Length of the base1 = 2 ft and length of the base2 = 4 ft and A = 6 ft²
We need to calculate the height of the trapezoid
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area =\(\frac{2 + 4}{2}\) × h
6 = \(\frac{6}{2}\) × h
6 = 3 × h
h = \(\frac{6}{3}\)
h = 2 ft

B. Substitute the given values in the formula.
= \(\frac{1}{2}\)h ( + )
Answer:
Given, Length of the base1 = 2 ft and length of the base2 = 4 ft and A = 6 ft^{2
6 = \(\frac{6}{2}\) × h}

Explanation:
By Substituting the given values in the formula
The answer is 6 = \(\frac{6}{2}\) × h

C. Simplify.
= h
Answer:
6 = \(\frac{6}{2}\) × h
6 = 3 × h
h = \(\frac{6}{3}\)
h = 2 ft

D. Divide.
h =
Answer:
h = 2 ft

Explanation:
The height of the trapezoid = 2 ft.

E. The height of the tabletop is feet.
Answer:
h = 2 ft

Explanation:
The height of the tabletop is 2 feet.

Check Understanding

Question 1.
A patch on a denim jacket is in the shape of the trapezoid shown. Find its area.

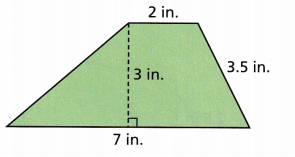
Answer:
Given length of the base1 = 7 in and base2 = 2 in.
height = 3 in.
Area of the trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{7 + 2}{2}\) × 3
Area = \(\frac{9}{2}\) × 3
Area = 13.5 in²

Question 2.
In a trapezoid, the length of one base is equal to the height and the length of the other base is twice the height. If the height is 10 centimeters, what is the area of the trapezoid? Explain how you found your answer.
Answer:
Area = 150 square centimeters.

Explanation:
Given, length of base a = height
length of the other base = 2h = 2 × 10 = 20 cm
height = 10 cm
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{10 + 20}{2}\) × 10
Area = \(\frac{10 + 20}{2}\) × 10
Area =\(\frac{30}{2}\) × 10
Area = 15 × 10
Area = 150 square centimeters.

Question 3.
A trapezoid has an area of 24 square feet. If the height is 6 feet, what is the sum of the lengths of the bases in feet?
Answer:
The sum of the lengths of the bases in feet is 8 feet.

Explanation:
Area = 24  sq feet, height = 6 feet
Area of a trapezoid = \(\frac{a + b}{2}\) × h
24 = \(\frac{a + b}{2}\) × 6
24 × 2 = 6 (a +b)
48 = 6 (a +b)
a + b = \(\frac{48}{6}\)
a + b = 8 feet.
The sum of the lengths of the bases in feet is 8 feet.

On Your Own

Question 4.
Reason The height of a trapezoid is \(\frac{1}{4}\) the sum of the lengths of its bases. The height is 2\(\frac{1}{2}\) feet. Find the area of the trapezoid. Show your work.
Answer:
Area = 12.5 square feet.

Explanation:
Given,
Height of a trapezoid = \(\frac{1}{4}\) (a +b)
height = 2\(\frac{1}{2}\) feet
2\(\frac{1}{2}\) = \(\frac{1}{4}\) (a +b)
\(\frac{5}{2}\) = \(\frac{1}{4}\) (a +b)
5 × 4 = 2 ( a + b)
20 = 2 ( a + b)
a + b = 10 feet.
Area of the trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{10}{2}\) × \(\frac{5}{2}\)
Area = 12.5 square feet.

Question 5.
STEM Many bridges use trapezoids structurally, because they can be made up of triangles, which are strong and rigid. For the bridge shown, if the top is 30 feet long, the bottom is 40 feet long, and the bridge has a height of 15 feet, what is the area of the side of the bridge?

Answer:
Given, that the base = is 30 feet, the bottom = is 40 feet and the height is 15 feet.
Area of the trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{30 + 40}{2}\) × 15
Area = \(\frac{70}{2}\) × 15
Area = 525 square feet.

Question 6.
One base of a trapezoid measures 12 meters, and the other base measures 8 meters. If the area is 144 square meters, what is the height of the trapezoid?
Answer:
The height of the trapezoid is = 14.4 m.

Explanation:
Area = 144  sq m
a = 12 m and b = 8m
Area of a trapezoid = \(\frac{a + b}{2}\) × h
144 square meters = \(\frac{12 + 8}{2}\) × h
144 = \(\frac{20}{2}\) × h
144 = 10 h
h = 14.4 m

Question 7.
A trapezoid has a base that is 10.2 centimeters long and another base that is 9.8 centimeters long. Its height measures 5 centimeters. What is the area of the trapezoid?
Answer:
Area = 50 square cm.

Explanation:
Given,
a = 10.2 cm, b = 9.8 cm , height = 5 cm
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{10.2 + 9.8}{2}\) × 5
Area = \(\frac{20}{2}\) × 5
Area = 10 × 5
Area = 50 square cm.

Question 8.
A window frame in the shape of a trapezoid has bases 4 feet and 3 feet long. Its height is 3 feet. What is the area of the glass needed for the window?
Answer:
Area = 10.5 square feet.

Explanation:
Given,
a = 4 feet, b = 3 feet , height = 3 feet.
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{4 + 3}{2}\) × 3
Area = \(\frac{7}{2}\) × 3
Area = 10.5 square feet

Question 9.
A parallelogram has a height of 7 meters and an area of 35 square meters. What would the sum of the lengths of the bases be for a trapezoid with the same height and area as the parallelogram?
Answer:
Sum of the length = a + b = 5 + 5 = 10 m

Explanation:
Given,
height = 7 m and area = 35 sq m
Area of a parallelogram = b × h
35 = b × 7
b = \(\frac{35}{7}\)
b = 5 m
Now we need to calculate the area of the trapezoid = \(\frac{a + b}{2}\) × h
35 = \(\frac{a + b}{2}\) × h
35 = \(\frac{a + 5}{2}\) × 7
35 × 2 = (a + 5) × 7
70 = 7a + 35
70 -35 = 7a
35 = 7a
a = \(\frac{35}{7}\)
a = 5 m

For Problems 10-13, find the area of a trapezoid with the given measures.

Question 10.
b₁ = 16 m, b₂ = 8 m, h = 4.5 m
Answer:
Area = 54 m²

Explanation:
Given, b₁ = 16 m, b₂ = 8 m, h = 4.5 m
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{16 + 8}{2}\) × 4.5
Area = \(\frac{24}{2}\) × 4.5
Area = 12 × 4.5
Area = 54 m²

Question 11.
b₁ = 4\(\frac{1}{4}\) in., b₂ = 3\(\frac{3}{4}\) in., h = 2\(\frac{1}{2}\) in.
Answer:

Explanation:
Given, b₁ = 4\(\frac{1}{4}\) in, b₂ = 3\(\frac{3}{4}\) in, h = 3\(\frac{3}{4}\) in.
b₁ = \(\frac{17}{4}\) in, b₂ = \(\frac{15}{4}\) in, h = \(\frac{15}{4}\) in
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{32}{8}\) × \(\frac{15}{4}\)
Area = 15 m²

Question 12.
b₁ = 5\(\frac{1}{6}\) yd, b₂ = 3\(\frac{1}{3}\) yd, h = 8 yd
Answer:

Question 13.
b₁ = 3.5 cm, b₂ = 6.5 cm, h = 8.4 cm
Answer:

Question 14.
Critique Reasoning Cindy says that both quadrilaterals shown have the same area because the sum of their bases is the same. Mark says that the parallelogram has a larger area than the trapezoid. Who is correct? Why?

Answer:
Cindy is correct. The height of the parallelogram is equal to the height of the trapezoid.
Area of the parallelogram is 5h.
Area of the trapezoid is 10 h or divided by 2 or 3.5 h.

Question 15.
Open-Ended Draw two different trapezoids that each have an area of 16 square units. Make one of the trapezoids with vertical parallel sides.

Answer:

Question 16.
The sum of the lengths of the bases of a trapezoid is 15 inches. If the trapezoid’s height measures 8 inches, what is the area of the trapezoid?
Answer:
Area = 60 inch²

Explanation:
Given, the sum of the lengths of the base (a+b)= 15 inches and height = 8 inches.
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{a + b}{2}\) × 8
Area = \(\frac{15}{2}\) × 8
Area = 15 × 4
Area = 60 inch²

For Problems 17-20. find the height for each trapezoid.

Question 17.
b₁ = 2cm, b₂ = 6 cm, A = 24cm²
h = ___________
Answer:
h = 6 cm.

Explanation:
Given, b₁ = 2cm, b₂ = 6 cm, A = 24cm²
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{2 + 6}{2}\) × h
24 = \(\frac{8}{2}\) × h
24 = 4 × h
h = 6 cm.

Question 18.
b₁ = 5 ft, b₂ = 7ft, A = 48 ft²
h = ____________
Answer:
h = 8 ft.

Explanation:
Given, b₁ = 5 ft, b₂ = 7 ft, A = 48 ft²
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{5 + 7}{2}\) × h
48 = \(\frac{12}{2}\) × h
48 = 6 × h
h = 8 ft.

Question 19.
b₁ = 5m, b₂ = 3 m, A = 30m²
h = ___________
Answer:
h = 7.5 m

Explanation:
Given, b₁ = 5 m, b₂ = 3 m, A = 30 m²
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{5 + 3}{2}\) × h
30 = \(\frac{8}{2}\) × h
30 = 4 × h
h = 7.5 m

Question 20.
b₁ = 5 in., b₂ = 4in., A = 20.25 in²
h = ____________
Answer:
h = 20.25 in.

Explanation:
Given, b₁ = 5 in., b₂ = 4in., A = 20.25 in²
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{5 + 4}{2}\) × h
20.25 × 2 = 9 × h
h = \(\frac{40.5}{2}\)
h = 20.25 in.

I’m in a Learning Mindset!

How did I apply what I knew about parallelograms to write an area formula for a trapezoid?
Answer:

Lesson 12.3 More Practice/Homework

Question 1.
The Shanghai World Financial Center is one of the tallest buildings in the world. It features a large trapezoidal opening to allow wind to pass through. The opening is about 35 meters tall. It is about 40 meters along the bottom and 50 meters along the top. What is the approximate area of the opening?

Answer:
Given, height = 35 m, base = 40 m, top length = 50 m
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{40 + 50}{2}\) × 35
Area = \(\frac{90}{2}\) × 35
Area = 45 × 35
Area = 1575 square meters.

Question 2.
A trapezoid’s longer base is three times the length of its shorter base. If the trapezoid has an area of 32 square feet and a height of 4 feet, what is the length of each base?
Answer:
b = 3a
Area = 32 square feet, height = 4 feet
Area of a trapezoid = \(\frac{a + b}{2}\) × h
32 = \(\frac{a + 3a}{2}\) × 4
32 = \(\frac{4a}{2}\) × 4
32 = 8a
a = \(\frac{32}{8}\)
a = 4 feet.

Question 3.
Reason One base of a trapezoid is 4 inches long, and the other base is 6 inches long. The trapezoid’s area is 25 square inches. Do the measurements describe a unique trapezoid? Explain.
Answer:
Area = 25 square inches
a = 4 inches, b = 6 inches
Area of a trapezoid = \(\frac{a + b}{2}\) × h
25 = \(\frac{4 + 6}{2}\) × h
25 = \(\frac{10}{2}\) × h
25 = 5h
h = \(\frac{25}{5}\)
h = 5 inches.

Question 4.
Math on the Spot Find the area of the trapezoid shown.

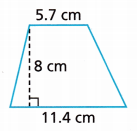
Answer:
Area = 68.4 cm.

Explanation:
Given, height = 8 cm
a = 11.4 cm, b = 5.7 cm
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{11.4 + 5.7}{2}\) × 8
Area = \(\frac{17.1}{2}\) × 8
Area = \(\frac{136.8}{2}\)
Area = 68.4 cm

Question 5.
The area of a trapezoid is 18 square feet. If the height is 3 feet, what is the sum of the lengths of the bases?
Answer:
The sum of the lengths of the base = 12 feet.

Explanation:
Given, height = 3 feet
Area = 18 square feet
Calculate the sum of the lengths of the base.
Area of a trapezoid = \(\frac{a + b}{2}\) × h
18 = \(\frac{a + b}{2}\) × 3
18 × 2 = 3 (a + b)
36 = 3 (a + b)
12 = a + b
The sum of the lengths of the base = 12 feet.

For Problems 6-9. find the area of each trapezoid.

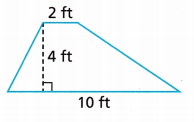
Question 6.

Answer:
Area = 18 square meters.

Explanation:
Given,
a = 10 ft, b = 2 ft and height = 4 ft
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{10 + 2}{2}\) × 4
Area = \(\frac{12}{2}\) × 3
Area =6 × 3
Area = 18 square meters.

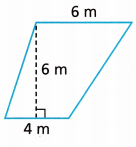
Question 7.

Answer:
Area = 15 square meters.

Explanation:
Given,
a = 4 m, b = 6 m and height = 6 m
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{4 + 6}{2}\) × 6
Area = \(\frac{10}{2}\) × 3
Area =5 × 3
Area = 15 square meters.

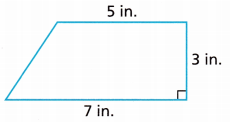
Question 8.

Answer:
Area = 18 Square in

Explanation:
Given,
a = 5 in, b = 7 in and height = 3 in
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{5 + 7}{2}\) × 3
Area = \(\frac{12}{2}\) × 3
Area =6 × 3
Area = 18 square in

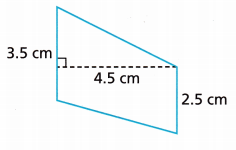
Question 9.

Answer:
Area = 13.5 square cm.

Explanation:
Given,
a = 3.5 cm, b = 2.5 cm and height = 4.5 cm
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{3.5 + 2.5}{2}\) × 4.5
Area = 13.5 square cm.

Test Prep

Question 10.
A trapezoid with which of these dimensions has the largest area?
(A) b₁ = 4 in., b₂ = 6 in., h = 8 in.
(B) b₁ = 8 in., b₂ = 3 in., h = 7 in.
(C) b₁ = 5 in., b₂ = 8 in., h = 6 in.
(D) b₁ = 6 in., b₂ = 9 in., h = 5 in.
Answer:
Option A with given dimensions has the largest area.

Explanation:
Let us check the given options to calculate the largest area.|
Given, b₁ = 4 in., b₂ = 6 in., h = 8 in
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Area = \(\frac{4 + 6}{2}\) × 8
Area = \(\frac{10}{2}\) × 8
Area = 5 × 8
Area = 40 square inches.
Option B has 38.5 square inches.
Option C has 39 square inches.
Option D has 37.5 square inches.
Hence by comparing all the given dimensions Option A with given dimensions has the largest area.

Question 11.
The sum of the lengths of the bases of a trapezoid is 6.4 meters. The trapezoid’s height is 4 meters. How many square meters is the area of the trapezoid?
Answer:
Given, that the sum of lengths of the base is 6.4 m
height is 4 m.

Question 12.
A trapezoid has an area of 36 square feet. If its height is 8 feet, and one base is 4 feet, what is the length of the other base?
Answer:
The length of the other base is 5 feet.

Explanation:
Area of a trapezoid = \(\frac{a + b}{2}\) × h
Given, Area = 36 square feet, height = 8 feet and base = 4 feet.
Area = \(\frac{a + 4}{2}\) × 8
36 = \(\frac{a + 4}{2}\) × 8
36 × 2 = (a + 4) × 8
72 = 8a + 32
40 = 8a
a = \(\frac{40}{8}\)
a = 5 feet.
The length of the other base is 5 feet.

Question 13.
Which of the following statements about a trapezoid with a height of 3 inches and an area of 54 square inches are true? Select all that apply.
(A) If one base is 6 inches long, the other base is 30 inches long.
(B) If one base is 9 inches long, the other base is 27 inches long.
(C) If one base is 12 inches long, the other base is 24 inches long.
(D) If one base is 18 inches long, the other base is 2 inches long.
(E) If one base is 36 inches long, the other base is 1 inch long.
Answer:
Option A. If one base is 6 inches long, the other base is 30 inches long
Option B. If one base is 9 inches long, the other base is 27 inches long.
Option C. If one base is 12 inches long, the other base is 24 inches long.

Explanation:
Given, height = 3 inches and area = 54 square inches.
area of a trapezoid = \(\frac{a + b}{2}\) × h
Now check the option A.
If one base is 6 inches long, the other base is 30 inches long.
area = \(\frac{6+30}{2}\) × 3
area = \(\frac{36}{2}\) × 3
area = 18 × 3
ara = 54 square inches.
next check option B.
If one base is 9 inches long, the other base is 27 inches long.
area = \(\frac{9+27}{2}\) × 3
area = \(\frac{36}{2}\) × 3
area = 18 × 3
area = 54 square inches.
Now check for option C.
If one base is 12 inches long, the other base is 24 inches long.
area = \(\frac{12+24}{2}\) × 3
area = \(\frac{36}{2}\) × 3
area = 18 × 3
area = 54 square inches.
therefore option A, B and C are following statements about a trapezoid with a height of 3 inches and an area of 54 square inches are true.

Spiral Review

Question 14.
An expression is shown.
\(\frac{3}{8}\) ÷ \(\frac{9}{16}\)
What is the value of the expression?
Answer:
\(\frac{2}{3}\).

Explanation:
let us solve the given expression
Given,
\(\frac{3}{8}\) ÷ \(\frac{9}{16}\)
\(\frac{3}{8}\) × \(\frac{16}{9}\)
The answer is \(\frac{2}{3}\).

Question 15.
Sue downloaded 20 songs for $25.00. What was the cost per song?
Answer:
$1.25

Explanation:
Given,
The cost for 20 songs is $25.
The cost per song is \(\frac{25}{20}\) = $1.25

Question 16.
An expression is shown.
11.57 – 6.2
What is the value of the expression?
Answer:
5.37

Explanation:
The value of the expression is 5.37.