Into Math Grade 6 Module 12 Lesson 2 Answer Key Develop and Use the Formula for Area of Triangles

We included HMH Into Math Grade 6 Answer Key PDF Module 12 Lesson 2 Develop and Use the Formula for Area of Triangles to make students experts in learning maths.

HMH Into Math Grade 6 Module 12 Lesson 2 Answer Key Develop and Use the Formula for Area of Triangles

I Can use the area formula for a triangle given either the base and height or the area and the height or the base.

Spark Your Learning

A farmer has a rectangular paddock for his horses, as shown. He wants to reconfigure his fields and change the paddock so that it is square. However, he wants it to have the same area as the rectangular paddock. What should the side length of the square paddock be? Justify your answer.


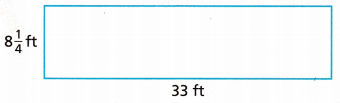
Answer:

Turn and Talk Will the rectangular paddock and the square paddock use the same amount of fencing? Explain.
Answer:

Build Understanding

A diagonal is a line segment that connects two nonadjacent vertices of a polygon.
Connect to Vocabulary
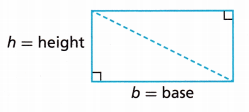
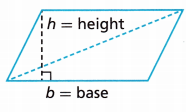
The base of a triangle can be any of its sides. The height of a triangle is the perpendicular distance from the base to the opposite vertex or side.

Question 1.
How can you find the area of a right triangle?
A. Recall that a rectangle is a quadrilateral with four right angles. The length and width of a rectangle also can be called the base and height.
You can put together two copies of a right triangle to form a rectangle as shown. What is the relationship between the rectangle and each right triangle?

Answer:
There is a rectangle in the given figure and in the rectangle has two right triangle.
Rectangle = 2 right triangle.

B. What is the area formula for a rectangle in terms of b and h?
Answer:
Area = b × h

Explanation:
The area formula for a rectangle in terms of b and h is b × h

C. How can you use the area formula for a rectangle to write an area formula for a right triangle?
Answer:
The Area of the Triangle is half the Area of the Rectangle.

Explanation:
Area of rectangle = l × b
Area of a right triangle is \(\frac{1}{2}\) × b × h

D. Write the area formula for a right triangle.

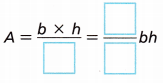
Answer:

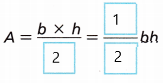
E. What is the area of the right triangle shown?

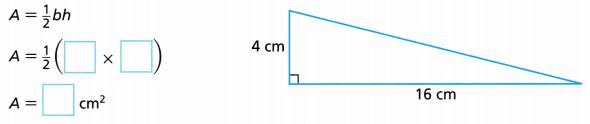
Answer:
Area of the triangle is 32 cm²

Explanation:

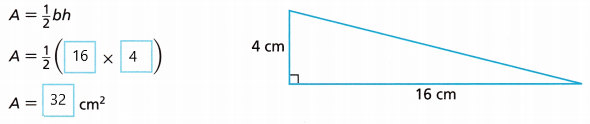
Turn and Talk Do you need to know the angle measures of a triangle to find its area? Explain.
Answer:

Question 2.
How can you find the area of a non-right triangle?
A. Recall that a parallelogram is a quadrilateral with two pairs of parallel sides. You can put together two copies of a non-right triangle to form a parallelogram as shown. What is the relationship between the parallelogram and each non-right triangle?

Answer:

B. What is the area formula for a parallelogram?
Answer:
A = b × h

Explanation:
The area formula for a parallelogram is b × h.

C. How can you use the area formula for a parallelogram to write an area formula for a triangle?
Answer:
Area of a parallelogram = 2 times the area of a triangle.

Explanation:
Area of a parallelogram = b × h
Area of a triangle = \(\frac{1}{2}\) × b × h
b × h = \(\frac{1}{2}\) × b × h
Therefore, the Area of a parallelogram is 2 times the area of a triangle.

D. Write the area formula for a triangle.

Answer:

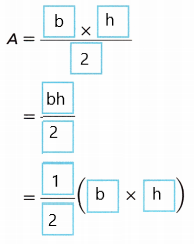
E. What is the area of the triangle shown?

Answer:
Area of the triangle is 30 in²

Step It Out

Question 3.
The height of a triangle is perpendicular to the base. Sometimes it is shown outside of the triangle. Find the length of the base in meters.

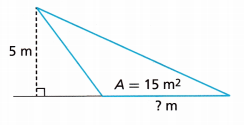
A. Substitute the known values into the formula for the area of a triangle.

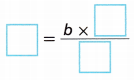
Answer:

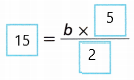
B. To solve for b, ___________ each side of the equation by \(\frac{2}{5}\).

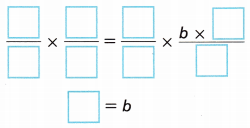
The base is _________ meters long.
Answer:
b = 6 m.

Explanation:

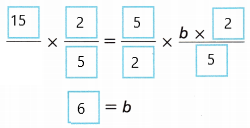
Question 4.
Many cities are planned with a grid pattern for the streets. Often there are one or more diagonal streets that cut across the grid, forming right triangles. What is the area within the triangle, in square feet?

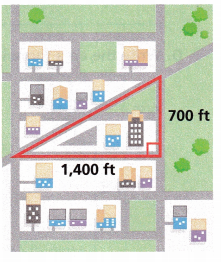
A. What are the dimensions of the triangle?
b = ft, h = ft
Answer:
b = 1400 ft, h = 700 ft

Explanation:
The dimensions of the triangle is b = 1400 ft, h = 700 ft.

B. Substitute the values for b and h into the formula for the area of a triangle. Then find the area.

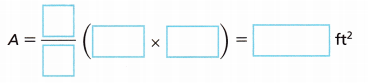
Answer:

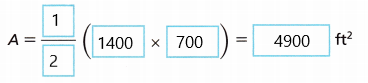
C. The area of the triangle is ____________ square feet.
Answer:
The area of the triangle is 4900 ft² 

Check Understanding

Question 1.
An isosceles right triangle has a base and height of 5 inches. Find its area.
Answer:
Given, a base and height of 5 inches.
The area of an isosceles right-angled triangle is \(\frac{l × l }{2}\)

Question 2.
Find the height of a triangle with an area of 12 square centimeters and a base of 8 centimeters.
Answer:
b = 3 centimeters.

Explanation:
Given,
base = 8 centimeters, Area = 12 square centimeters.
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
12 = \(\frac{1}{2}\) × 8 × h
h = \(\frac{12 × 2 }{8}\)
b = 3 centimeters.

On Your Own

Question 3.
Reason Doug is making square tiles as shown. What is the area of the smaller square in the figure? Explain.

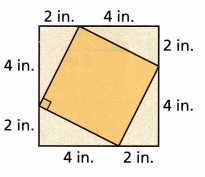
Answer:
Area = 4 inches²

Explanation:
Area of a triangle = \(\frac{1}{2}\) × b × h
b = 2 in and h = 4 in.
Therefore area of a triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 2 × 4
Area = 4 inches²
Hence in the given figure there are 4 smaller triangles.
The side of a square is 4 inches
Area of the smaller square in the figure = s × s
Area = 4 × 4
Area = 16 inches²

Question 4.
A triangle has a base measuring 8\(\frac{1}{2}\) inches. If its height is 4\(\frac{1}{2}\) inches, what is the area of the triangle?
Answer:
Area of the triangle = 19.12 inches²

Explanation:
Given, base = 8\(\frac{1}{2}\) = \(\frac{17}{2}\)
Height = 4\(\frac{1}{2}\) = \(\frac{9}{2}\) inches
area of the triangle = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × \(\frac{17}{2}\) × \(\frac{9}{2}\)
Area = \(\frac{17 × 9}{2 × 2 × 2}\)
Area = \(\frac{153}{8}\) inches
Area = 19.12 inches²

Question 5.
Walt is designing a school pennant in the shape of a triangle. The pennant must have a height of 11 inches and an area of 66 square inches. What must the length of the base be?

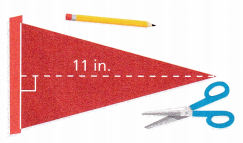
Answer:
b = 12 inches.

Explanation:
Given,
height = 11 inches, Area = 66 square inches.
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
66 = \(\frac{1}{2}\) × b × 11
b = \(\frac{66 × 2 }{11}\)
b = 12 inches.

Question 6.
A rectangle has a length of 8 feet and a width of 3 feet. If a right triangle has a height of 3 feet, what length would its base be if it has the same area as the rectangle?
Answer:
The base of the triangle is 8 feet.

Explanation:
Given, Length = 8 feet and width = 3 feet
Height of a right triangle = 3 feet
Also given the Area of a rectangle is equal to the area of the triangle.
Now simplify
Area of a rectangle = l × b
Area = 8 × 3
Area = 24 feet²
Now calculate the base
area of the triangle = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
24 = \(\frac{1}{2}\) × b × 3
b = 8 feet

Question 7.
A triangular roof is built so that its height is half its base. If the base of the roof is 32 feet long, what is the area of the roof?
Answer:
Area of the roof = 306.25 feet²

Explanation:
Given,
height = \(\frac{1}{2}\) × b, base = 35 feet.
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 35 × \(\frac{1}{2}\) × 35
Area = \(\frac{35 × 35 }{2 × 2}\)
Area = \(\frac{35 × 35 }{4}\)
Area = 306.25 feet²

Question 8.
A triangle has a height of 7 inches and an area of 35 square inches. What is the length of the base?
Answer:
The length of the base is 10 inches.

Explanation:
Given,
height = 7 inches, area = 35 square inches.
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
35 = \(\frac{1}{2}\) × b × 7
35 = \(\frac{b × 7 }{2}\)
b = \(\frac{35 × 2 }{7}\)
b = 10 inches.
The length of the base is 10 inches.

For Problems 9-12, find the area of a triangle with the given base and height.

Question 9.
b = 12 m, h = 6.5 m
Answer:
b = 39 m.

Explanation:
Given,
height = 6.5 m, b = 12 m
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 12 × 6.5
Area = \(\frac{12 × 6.5 }{2}\)
b = 39 m.

Question 17.
A = 34 ft², h = 8.5 ft
Answer:
b = 8.5 ft

Explanation:
Given,
height = 8.5 ft, area = 34 ft²
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
34 = \(\frac{1}{2}\) × b × 8.5
34 = \(\frac{b × 6.5 }{2}\)
b = \(\frac{34 × 2 }{6.5}\)
b = 8.5 ft

Question 10.
b = 4 in., h = 8 in.
Answer:
Area = 16 in²

Explanation:
Given,
height = 8 in, b = 4 in
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 4 × 8
Area = \(\frac{4 × 8 }{2}\)
Area = 16 in²

Question 11.
b = 8 ft, h = 7 ft
Answer:
Area = 14 ft²

Explanation:
Given,
height = 7 ft, b = 8 ft
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 8 × 7
Area = \(\frac{8 × 7 }{2}\)
Area = 14 ft²

Question 12.
b = 4.4 cm, h = 6.5 cm
Answer:
Area = 14.3 cm²

Explanation:
Given,
height = 6.5 cm, b = 4.4 cm
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 4.4 ×6.5
Area = \(\frac{4.4 × 6.5 }{2}\)
Area = \(\frac{28.6}{2}\)  cm²
Area = 14.3 cm²

Question 13.
Critique Reasoning For the two triangles shown, Clara says that the triangle on the right has a larger area because the triangle on the left is narrower. Prisha says that both triangles have the same area. Who is correct? Why?

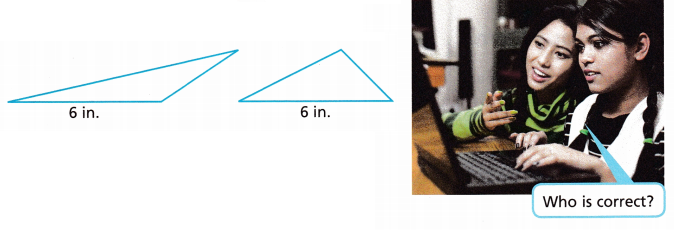
Answer:

Question 14.
Open-Ended Draw two different triangles so that each has an area of 10 square units.

Answer:

Question 15.
A triangle has an area of 7 square feet. What could be the length of the base and the height?
Answer:
Area of a square = 7 sq feet

For Problems 16-19, find the unknown base length for each triangle.

Question 16.
A = 44 cm², h = 11 cm
Answer:
b = 8 cm

Explanation:
Given,
height = 11 m, area = 44 cm²
The area of the triangle is \(\frac{1}{2}\) × b × h
44 = \(\frac{1}{2}\) × b × h
44 = \(\frac{1}{2}\) × b × 11
b = \(\frac{44 × 2 }{11}\)
b = 8 cm

Question 17.
A = 34 ft², h = 8.5 ft
Answer:
b = 8 cm

Explanation:
Given,
height = 8.5 ft, area = 34 ft²
The area of the triangle is \(\frac{1}{2}\) × b × h
34 = \(\frac{1}{2}\) × b × h
34 = \(\frac{1}{2}\) × b × 8.5
b = \(\frac{34 × 2 }{8.5}\)
b = 8 cm

Question 18.
A = 49 m², h = 7 m
Answer:
b = 14 m.

Explanation:
Given,
height = 7 m, area = 49 m²
The area of the triangle is \(\frac{1}{2}\) × b × h
49 = \(\frac{1}{2}\) × b × h
49 = \(\frac{1}{2}\) × b × 7
b = \(\frac{49 × 2 }{7}\)
b = 14 m.

Question 19.
A = 31.5 in², h = 7 in.
Answer:
b = 9 in.

Explanation:
Given,
height = 7 in, area = 31.5 in²
The area of the triangle is \(\frac{1}{2}\) × b × h
31.5 = \(\frac{1}{2}\) × b × h
31.5 = \(\frac{1}{2}\) × b × 7
b = \(\frac{31.5 × 2 }{7}\)
b = \(\frac{63}{7}\)
b = 9 in.

I’m in a Learning Mindset!

What questions can I ask to help me understand how to find the area of a right triangle?
Answer:

Lesson 12.2 More Practice/Homework

Question 1.
STEM A geodesic dome is made up of triangles, most of which are equilateral. The surface uses less material and allows for more open space than traditional buildings. An equilateral panel of a geodesic dome has a base of 6 feet and a height of about 5.2 feet. What is its area in square feet?

Answer:

Question 2.
Reason A triangle has a height of 3 meters and an area of 9 square meters. Is there a unique triangle represented by these measurements? Explain.
Answer:
b = 6 m

Explanation:
Given,
height = 3 m, area = 9 square meters
The area of the triangle is \(\frac{1}{2}\) × b × h
9 = \(\frac{1}{2}\) × b × h
9 = \(\frac{1}{2}\) × 3 × b
6 m = b

Question 3.
An isosceles right triangle has a base and height with the same length. It the area of the triangle is 32 square centimeters, how long are the base and height?
Answer:
8 cm

Explanation:
Given
Base = L and height = L
area of triangle = 32 square centimeters
Area of an isosceles right triangle = \(\frac{L × L}{2}\)
Now simplify the equation
32 = \(\frac{L × L}{2}\)
64 = L²
L = 8 cm

Question 4.
Math on the Spot The diagram shows the outline of the triangular foundation of a front porch. What is the area of the foundation?

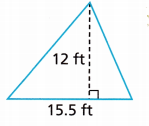
Answer:
93 ft²

Explanation:
Given,
height = 12 ft, base = 15.5 ft
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 15.5 × 12
Area = 93 ft²

For Problems 5-8, find the area.

Question 5.

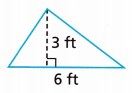
Answer:
9 ft²

Explanation:
Given,
height = 3 ft, base = 6 ft
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 6 × 3
Area = 9 ft²

Question 6.

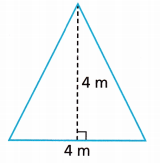
Answer:
8 m²

Explanation:
Given,
height = 4 ft, base = 4 ft
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 4 × 4
Area = 8 m²

Question 7.

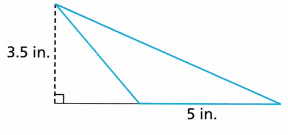
Answer:
8.75 m²

Explanation:
Given,
height = 3.5 in, base = 5 in
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 3.5 × 5
Area = \(\frac{1}{2}\) × 17.5 m²
Area = 8.75 m²

Question 8.

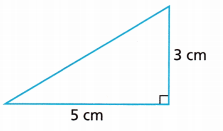
Answer:
7.5 sq. cm

Explanation:
Given,
height = 3 cm, base = 5 cm
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 3 × 5
Area = \(\frac{1}{2}\) × 15 m²
Area = 7.5 m²

Test Prep

Question 9.
Which triangle has the largest area?

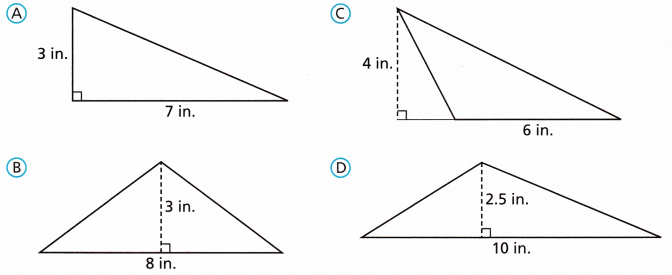
Answer:

Question 10.
A triangle has a base that measures 6.4 feet. Its height measures 5 feet. How many square feet is the area of the triangle?
Answer:
16 feet²

Explanation:
Given base = 6.4 feet
Height = 5 feet
The area of the triangle is \(\frac{1}{2}\) × b × h
Area = \(\frac{1}{2}\) × 5 × 6.4
Area = \(\frac{32}{2}\)
Area = 16 feet².

Question 11.
A triangle has an area of 42 square feet. If the height of the triangle is 4 feet, how many feet is the length of the base?
Answer:
Given Area = 42 square feet
Height = 4 feet
The area of the triangle is \(\frac{1}{2}\) × b × h
42 = \(\frac{1}{2}\) × b × 4
42 = 2b
b = \(\frac{42}{2}\)
b = 21 feet.

Question 12.
The height of a triangle is one-tenth of its base. The base measures 12 inches. How many square inches is the area of the triangle?
Answer:
Area = \(\frac{6}{5}\) inches²

Explanation:
h = \(\frac{1}{10}\) × b
base = 12 inches
h = \(\frac{1}{10}\) × 12
h = \(\frac{6}{5}\)
The area of the triangle is \(\frac{1}{2}\) × b × h
area = \(\frac{1}{2}\) × 12 × \(\frac{6}{5}\)
Area = \(\frac{36}{5}\)
Area = \(\frac{36}{5}\) inches²
Area = 7.2 inches.

Spiral Review

Question 13.
An equation is shown.
64x = 8
What is the value of x that makes the equation true?
Answer:
8

Explanation:
The value of x that makes the equation true is 8.
64x =8
x = \(\frac{64}{8}\)
x = 8

Question 14.
An expression is shown.
2\(\frac{3}{4}\) ÷ 4\(\frac{1}{2}\)
What is the value of the expression?
Answer:
0.611

Explanation:
Given,
2\(\frac{3}{4}\) ÷ 4\(\frac{1}{2}\)
\(\frac{11}{4}\) ÷ \(\frac{9}{2}\)
\(\frac{11}{4}\)×\(\frac{2}{9}\)
\(\frac{11}{2}\) ×\(\frac{1}{9}\)
0.611