We included HMH Into Math Grade 6 Answer Key PDF Module 12 Lesson 1 Develop and Use the Formula for Area of Parallelograms to make students experts in learning maths.
HMH Into Math Grade 6 Module 12 Lesson 1 Answer Key Develop and Use the Formula for Area of Parallelograms
I Can understand the area formula for a parallelogram and use it to find area or to find unknown dimensions given the area.
Spark Your Learning
The tabletops in a restaurant are parallelograms and rectangles with the same distance between parallel sides. The approximate side lengths are shown. Is the area of a parallelogram-shaped tabletop the same as the area of a rectangular one? Explain.

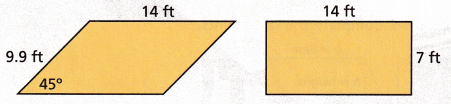
Answer:
Turn and Talk Suppose the restaurant also has square tabletops. What are the approximate side lengths of one of the square tabletops if it has the same area as the rectangular tabletop? Explain.
Answer:
Build Understanding
A quadrilateral is a polygon with four sides and four angles. If it has two pairs of sides that are parallel, it is a parallelogram.
Answer:
From the given question, a rectangle has two pairs of opposite sides and are parallel, and four right angles. It is also called a parallelogram as it has two pairs of parallel sides. A square has two pairs of parallel sides, four right angles, and all four sides are equal. Therefore it is also called a rectangle and a parallelogram.
Question 1.
How can you find the area of a parallelogram?
A. Look at the parallelogram shown. If you draw a line to make a right triangle and then move the right triangle as shown, it forms a new figure. What is the new figure?
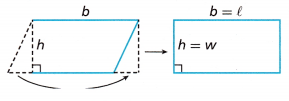
Answer:
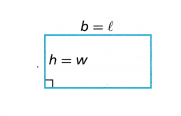
B. Look at the quadrilaterals shown. Complete the statements.
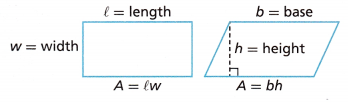
To find the area of a rectangle, multiply its ____________ by its __________. The area of a parallelogram is found by multiplying its __________ by its ____________.
Answer:
To find the area of a rectangle, multiply its length by its width. The area of a parallelogram is found by multiplying its base by its height.
C. Why are the area equations in Part B so alike?
In the quadrilaterals in Part B, the length of the rectangle is equal to the ____________ of the parallelogram, and the width of the rectangle is equal to the ___________ of the parallelogram.
Answer:
In the quadrilaterals in Part B, the length of the rectangle is equal to the base of the parallelogram, and the width of the rectangle is equal to the height of the parallelogram.
D. Since b = ![]() and h =
and h = ![]() , and since A = Lw for a rectangle, then
, and since A = Lw for a rectangle, then
A = ![]() ×
× ![]() for a parallelogram.
for a parallelogram.
Answer:
b = l and h = w
A = l × w for a parallelogram
Explanation:
Given, b = l and h = w
A = l × w for a parallelogram
E. What is the area of the parallelogram shown?
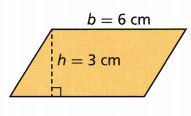
A = bh
A = ![]() cm ×
cm × ![]() cm
cm
A = ![]() cm2
cm2
Answer:
A = 6 cm × 3 cm
A = 18 cm2
Explanation:
The area of a parallelogram is A = b × h
Area = 18 cm2
Turn and Talk Explain how the area of the rectangle and the area of the parallelogram in Part B compare.
Answer:
Step It Out
Question 2.
A floor is made up of parallelogram-shaped tiles that each have a base length of 8.5 inches and a height of 3.5 inches. What is the area of each tile in square inches?

A. What is the formula for the area of a parallelogram?
Answer:
A = b × h
Explanation:
The area of a parallelogram is A = b × h
B. What are the dimensions of the parallelogram?
b = ![]() in. h =
in. h = ![]() in.
in.
Answer:
8.5 in, 3.5 in
Explanation:
The dimensions of the parallelogram b = 8.5 in, height = 3.5 in.
C. Substitute the values for b and h into the formula:
A = ![]() in. ×
in. × ![]() in.
in.
Answer:
A = 8.5 in × 3.5 in
29.75 in2
Explanation:
The area of a parallelogram is A = b × h
A = 8.5 in × 3.5 in
D. Find the area:
A = ![]() in2
in2
Answer:
29.75 in2
Explanation:
A = 8.5 in × 3.5 in
A = 29.75 in2
E. Each tile has an area of ___________ square inches.
Answer:
29.75 in2
Explanation:
Each tile has an area of 29.75 in2 square inches
Question 3.
The Louvre Pyramid has a square base with the dimensions shown. What is the area of the base in square meters?

A. How is a square a special rectangle?
Answer:
B. For a rectangle, A = l × w. If the side of a square is s, then A = ![]() ×
× ![]() =
= ![]() .
.
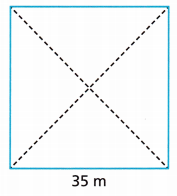
Answer:
A = 35 × 35
C. For the Louvre Pyramid, s = ![]() m.
m.
Answer:
s = 35 m
Explanation:
For the Louvre Pyramid, s = 35 m.
D. Substitute the value for s into the formula:
A = ![]() 2
2
Answer:
A = 352
E. Find the area:
A = ![]() m2
m2
Answer:
1225 m2
F. The area of the base of the Louvre Pyramid is ___________ square meters.
Answer:
1225 m2
Explanation:
The area of the base of the Louvre Pyramid is 1225 m2 square meters.
Turn and Talk Since a square is a rhombus, can you use the same area formula for any rhombus as for a square? Explain.
Answer:
The square is a shape that has four equal angles of 90 degrees. Therefore a square is a rhombus. However, a rhombus is not a square as their areas cannot be the same.
Question 4.
Harry is building a garden in the shape of a parallelogram that is 24 feet long. The garden will not be rectangular, though, so he’s not sure how wide it can be. He has enough materials to cover 84 square feet. How many feet wide can the garden be?

A. What is the equation for the area of a parallelogram?
A = ![]() ×
× ![]()
Answer:
A = b × h
Explanation:
The area of a parallelogram is A = b × h
B. Substitute the known values.
![]() =
= ![]() × h
× h
Answer:
84 ft2 = 24 ft × h
h = 3.5 ft
Explanation:
The known values are Area = 84 ft84 ft2 = 24 ft × h
h = 3.5 ft , base = 24 ft.
A = b × h
84 ft2 = 24 ft × h
h = 3.5 ft
C. To solve for h, __________ each side of the equation in Part B by ![]() .
.
Answer:
Divide the equation on both by 24
Explanation:
To solve for h,
Each side of the equation in part B by 24.
\(\frac{84}{24}\)
3.5 ft = h
D. Substitute the known values. Then solve.
h = 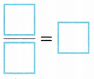
Answer:
3.5 feet
Explanation:
h = 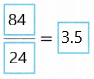
E. The garden can be __________ feet wide.
Answer:
3.5 feet wide
Explanation:
The garden can be 3.5 feet wide.
Check Understanding
Question 1.
A company logo is in the shape of the parallelogram shown. Find its area.
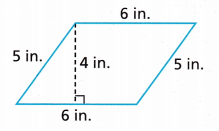
Answer:
24 inches2.
Explanation:
Given, height = 4 in, base = 6 in
A = b × h
A = 6 × 4
A = 24 inches2.
Question 2.
A square has a side length of 1.2 meters. What is its area in square meters?
Answer:
1.44 m2.
Explanation:
Given side length = 1.2 m.
Area of a square = s
Area = 1.2 × 1.2
Area = 1.44 m2
Question 3.
Find the length of the base of the parallelogram shown.
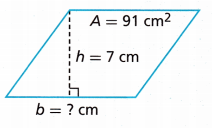
Answer:
b = 13 cm.
Explanation:
Given area = 91 cm2.
h = 7 cm.
Area of parallelogram = b × h
Now simplify the equation
91 = b × 7
b = 13 cm.
On Your Own
Question 4.
Reason The height of a parallelogram is 4 times its base. The base measures 2\(\frac{1}{2}\) feet. Find the area of the parallelogram. Show your work.
Answer:
25 feet2.
Explanation:
h = 4b
b = 2\(\frac{1}{2}\) feet = \(\frac{5}{2}\) feet
Area of parallelogram = b × h
h = 4 × \(\frac{5}{2}\)
h = 10 feet.
h = 4b
10 = 4 × b
b = \(\frac{10}{4}\)
b = 2.5 feet
area = 2.5 × 10
Area = 25 feet2
Question 5.
On a baseball field, the area inside the base path is the infield. For a major league field, the infield must be a square that is 90 feet on each side, and each base is a corner of the square. What is the area of the infield in square feet?
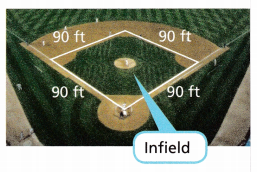
Answer:
Question 6.
A parallelogram has an area of 125 square inches. If it is 25 inches long, what is the height in inches?
Answer:
Height = 5 inches.
Explanation:
Given Area = 125 square inches.
base = 25 inches
Now calculate height in inches
Area of parallelogram = b × h
125 = 25 × h
h = 5 inches
Question 7.
A parallelogram has a base that is 10.2 centimeters long and a height that measures 5 centimeters. What is the area of the parallelogram?
Answer:
51 cm2
Explanation:
Given base = 10.2 cm
height = 5cm
Area of parallelogram = b × h
Area = 10.2 × 5
Area = 51 cm2
Question 8.
A window is the shape of a rhombus, with each side being 20 inches long. The height of the window is 16 inches. What is the area in square inches of the glass needed for the window?
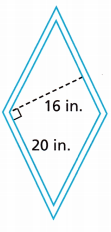
Answer:
Question 9.
Open-Ended A rectangle has an area of 35 square meters. What could its length and width be?
Answer:
For Problems 10-13, find the area of a parallelogram with the given base and height.
Question 10.
b = 10 m
h = 4.5 m
Answer:
45 m
Explanation:
Given b = 10 m.
base = 4.5 m
Now calculate the Area of a parallelogram
Area of parallelogram = b × h
Area = 10 × 4.5
Area = 45 m2.
Question 11.
b = 3\(\frac{1}{4}\) in.
h = 2\(\frac{1}{2}\) in.
Answer:
8.125 in2
Explanation:
Given b = 3\(\frac{1}{4}\) = \(\frac{13}{4}\)
base = 2\(\frac{1}{2}\) = \(\frac{5}{2}\)
Now calculate the Area of a parallelogram
Area of parallelogram = b × h
Area = \(\frac{13}{4}\) × \(\frac{5}{2}\)
Area = \(\frac{65}{8}\)
Area = 8.125 inches2
Question 12.
b = 8\(\frac{1}{6}\) yd
h = 2\(\frac{4}{7}\) yd
Answer:
21 yd2.
Explanation:
Given, b = 8\(\frac{1}{6}\) = \(\frac{49}{6}\)
h = 2\(\frac{4}{7}\) yd = \(\frac{18}{7}\)
Now calculate the Area of a parallelogram
Area of parallelogram = b × h
Area = \(\frac{49}{6}\) × \(\frac{18}{7}\)
Area = 7 × 3
Area = 21 yd2
Question 13.
b = 2.4 cm
h = 6.5 cm
Answer:
15.6 cm2
Explanation:
Given, b = 2.4 cm
h = 6.5 cm
Now calculate the Area of a parallelogram
Area of parallelogram = b × h
Area = 2.4 × 6.5
Area = 15.6 cm2.
Question 14.
Critique Reasoning For the two quadrilaterals shown, Dan says that the one on the left has a larger area than the one on the right because it is longer. Bob says that both quadrilaterals have the same area. Who is correct? Why?

Answer:
Question 15.
Open-Ended Draw two different parallelograms that each have an area of 12 square centimeters. Then give the base and height of each parallelogram.
Answer:
Question 16.
A square has an area of 144 square inches. How long is each side of the square?
Answer:
Side of the square = 12 inches.
Explanation:
Given,
Area of square = 144 square inches.
Area of square = S2
144 = S2
S = 12 inches.
For Problems 17-18, find the unknown height for each parallelogram.
Question 17.
b = 9 cm
A = 108 cm2
h = ____________
Answer:
12 cm.
Explanation:
Given,
b = 9 cm
A = 108 cm2
Area of parallelogram = b × h
108 cm2 = 9 × h
h = \(\frac{108}{9}\)
h= 12 cm.
Question 18.
b = 8.5 ft
A = 68 ft2
h = ____________
Answer:
8 ft.
Explanation:
Given,
b = 8.5 ft
A = 68 ft2
Area of parallelogram = b × h
68 = 8.5 × h
h = \(\frac{68}{8.5}\)
h = 8 ft.
I’m in a Learning Mindset!
What is challenging about finding the area of a parallelogram?
Answer:
Lesson 12.1 More Practice/Homework
Question 1.
Reason A parallelogram’s base is twice its height. If the parallelogram has an area of 32 square feet, what are the lengths of the base and height?
Answer:
b = 4 feet , h = 8 feet
Explanation:
Given,
b = 2h
Area = 32 square feet
Area of parallelogram = b × h
32 square feet = 2h × h
32 = 2h2
16 = h2
h = 4
b = 2 × 4
b = 8 feet
Question 2.
Construct Arguments Which parallelogram has the greater area? Explain.
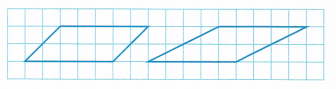
Answer:
Question 3.
A panel in a stained-glass window in the shape of a parallelogram has the dimensions shown. Find the area of the panel.
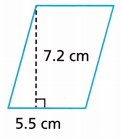
Answer:
39.6 cm2
Explanation:
Given, base = 5.5 cm and height = 7.2 cm
Area of parallelogram = b × h
Area = 5.5 × 7.2
Area = 39.6 cm2.
For Problems 4-7, find the area of the figure.
Question 4.
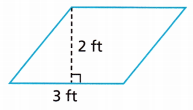
Answer:
6 f2
Explanation:
Given,
Base = 3 ft, Height = 2 ft
Area of parallelogram = b × h
Area = 3 × 2
Area = 6 ft2.
Question 5.

Answer:
28.5 in2
Explanation:
Given,
Base = 9.5 in, Height = 3 in.
Area of parallelogram = b × h
Area = 9.5 × 3
Area = 28.5 in2.
Question 6.
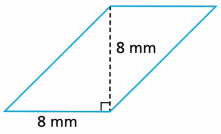
Answer:
64 mm2.
Explanation:
Given,
Base = 8 mm, Height = 8 mm.
Area of parallelogram = b × h
Area of parallelogram = 8 × 8
Area = 64 mm2.
Question 7.
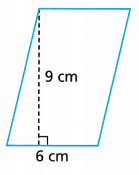
Answer:
54 cm2.
Explanation:
Given,
Base = 9 cm, Height = 6 cm.
Area of parallelogram = b × h
Area of parallelogram = 9 × 6
Area = 54 cm2.
Test Prep
Question 8.
Which quadrilateral has the largest area?
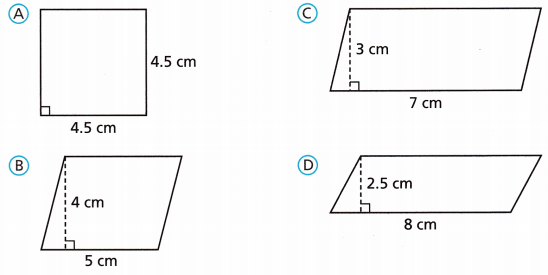
Answer:
Question 9.
A parallelogram has a base that measures 4.8 meters. Its height measures 5 meters. How many square meters is the area of the parallelogram?
Answer:
24 m2.
Explanation:
Given, base = 4.8 m, height = 5 m
Area of parallelogram = b × h
Area = 4.8 × 5
Area = 24 m2.
Question 10.
A parallelogram has an area of 37 square feet. If the height of the parallelogram is 4 feet, how many feet is the base?
Answer:
9.25 feet.
Explanation:
Given, area = 37 square feet, height = 4 feet.
Area of parallelogram = b × h
Now simplify the area of parallelogram
Area = b × h
37 = b × 4
b = \(\frac{37}{4}\)
b = 9.25 feet
Question 11.
The base of a parallelogram is half its height. The base measures 6\(\frac{1}{2}\) inches. Find the area of the parallelogram in square inches.
Answer:
13 inches.
Explanation:
b = 1/2 h
b = 6\(\frac{1}{2}\)
b = \(\frac{13}{2}\)
Now simplify,
b = \(\frac{1}{2}\) × h
\(\frac{13}{2}\) = \(\frac{1}{2}\) × h
h = 13 inches.
Spiral Review
Question 12.
Write two expressions that are equivalent to 4(6x + 8y).
Answer:
24x + 32y and 12x + 16y.
Explanation:
The two expressions that are equivalent to 4(6x + 8y) is 24x + 32y and 12x + 16y.
Question 13.
Show that 9.1 is not a solution of the equation n – 6.4 = 2.61. Then find the solution.
Answer:
The solution for the given question is 9.01
Explanation:
The given equation is
n – 6.4 = 2.61
n = 2.61 + 6.4
n = 9.01
Hence 9.1 is not a solution of the given equation.
Question 14.
An expression is shown.
3.4 × 6.25
What is the value of the expression?
Answer:
21.25
Explanation:
The value of the given expression is 21.25.