We included HMH Into Math Grade 6 Answer Key PDF Module 11 Lesson 3 Find Distance on the Coordinate Plane to make students experts in learning maths.
HMH Into Math Grade 6 Module 11 Lesson 3 Answer Key Find Distance on the Coordinate Plane
I Can find the distance between two points with the same x- ory-coordinate across quadrants and use a scale in real-world problems to find actual distances.
Spark Your Learning
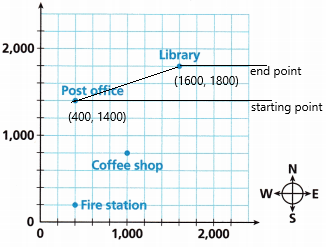
Nestor is bicycling around the city. All the streets in his neighbourhood are in a grid. The grid provided shows the locations of several landmarks. Each side of a square on the grid represents 200 meters. Nestor wants to ride from the library to the coffee shop, staying on the roads. What is the length of the shortest route he can take?

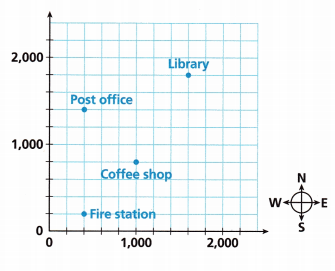
Answer:
– Now we write the vertices first.
– The coordinates of the library are (1600, 1800)
– The coordinates of the post office are (400, 1400)
– The coordinates of a coffee shop are (1000, 800)
– The coordinates of the fire station are (400, 200)
Now we have to find out the shortest distance.
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
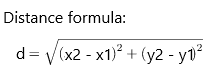
The distance from library to the coffee shop:
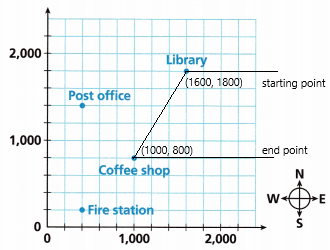
A = (x1, y1)
A = (1600, 1000)
B = (x2, y2)
B = (1800, 800)
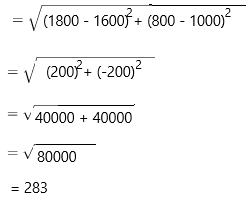
The distance between the given points is 283.
Turn and Talk Explain how you can find the total distance that Nestor needs to bicycle to get from the post office to the library.
Answer:
– The coordinates of the library are (1600, 1800)
– The coordinates of the post office are (400, 1400)
Now we have to find out the shortest distance.
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
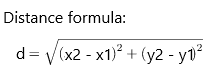
A = (x1, y1) = (400, 1600)
B = (x2, y2) = (1400, 1800)
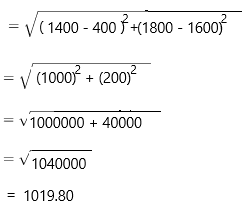
The distance between the given points is 1019.80
Build Understanding
A point on a coordinate plane can be reflected across an axis. The reflection is located on the opposite side of the axis, at the same distance from the axis.

Connect to Vocabulary
A reflection of a figure is a transformation of the figure that flips the figure across a line.
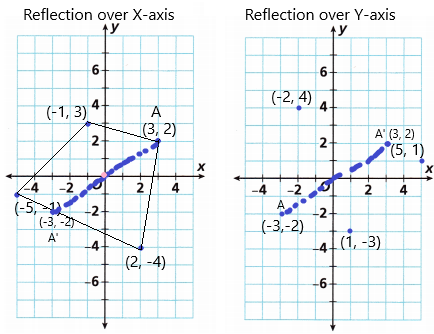
Question 1.
Use the table to record your work.

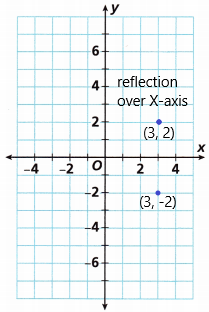
A. Draw a coordinate plane on graph paper. Graph the point (3, -2) on your grid. Fold the paper along the y-axis and look through the paper to see where the point falls to find the location of the reflection of (3, -2) across the y-axis. Record the coordinates of the reflection in the table.
Answer:
When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates is transformed into their opposite signs.
Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
The reflection of the point(3, -2) across the Y-axis is (-3, -2)
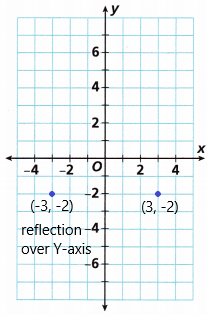
B. Unfold the paper, and fold the paper along the x-axis to find the location of the reflection of (3, -2) across the x-axis. Record the coordinates of the reflection in the table.
Answer:
When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs.
Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
The reflection of the point (3, -2) across the X-axis is (3, 2)
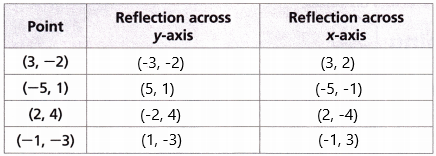
C. Repeat this process with the other three points in the table.
Answer:
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
According to the above rules, we can write the reflection of points. The table is filled and shown below:
D. What is the relationship between the coordinates of a point and the coordinates of its reflection across each axis?
Answer:
Coordinates of a point:
The coordinates of a point are a pair of numbers that define its exact location on a two-dimensional plane. Recall that the coordinate plane has two axes at right angles to each other, called the X and Y- axis The coordinates of a given point represent how far along each axis the point is located.
Reflection:
a reflection is known as a flip. A reflection is a mirror image of the shape. An image will reflect through a line, known as the line of reflection. A figure is said to be a reflection of the other figure, and then every point in a figure is equidistant from each corresponding point in another figure. The reflected image should have the same shape and size, but the image faces in the opposite direction.
coordinates of its reflection across each axis:
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
E. Why do you think this transformation is called reflection?
Answer:
When the size of a shape is increased or reduced then the image of the shape will be similar to the pre-image. The similar figures have dimensions equal in proportion. But in the case of congruent, the transformation of objects is done by using rotation, reflection or translation. The shape is turned or flipped to transform into another shape.
This type of translation is called reflection because it flips the object across a line by keeping its shape or size constant.
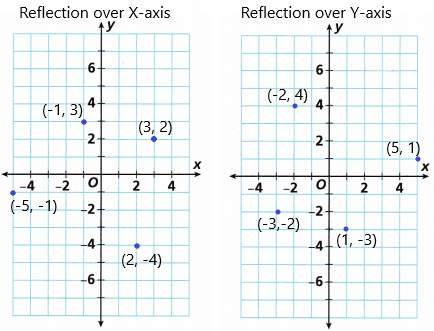
Turn and Talk A point is reflected first across the x-axis and then across the y-axis. How will the coordinates of the final point be related to the coordinates of the original point? Explain.
Answer:
In the coordinate plane, we can use any point as the point of reflection. The most commonly used point is the origin. When you draw a line segment connecting the points A and A’, the origin should be the midpoint of the line. Therefore, the point of reflection is the origin (0, 0), and the image of the point (x, y) is (-x, -y).
Hence, the coordinate of points A’ of reflection over X-axis is (-3, -2)
the coordinates of points A’ of reflection over Y-axis is (3,2)
Step It Out
Question 2.
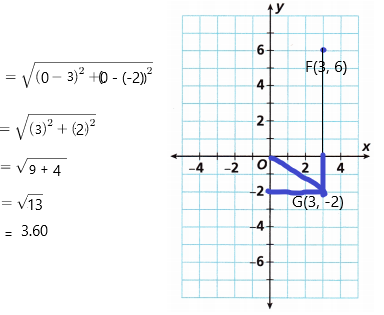
What is the distance between the two points on the coordinate plane, measured by units of the coordinate plane?
A. Plot and label Points F{3, 6) and G(3, -2) on the coordinate plane.
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
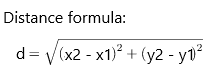
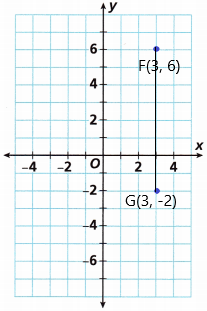
The coordinates of F = (x1, y1) = (3, 3)
The coordinates of G = (x2, y2) = (6, -2)
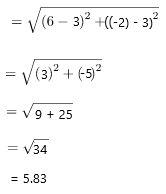
Therefore, the distance is 5.83
B. The x-coordinate of Point F is ___________ as the x-coordinate of Point G.
Answer:
The coordinate point F (3, 6)
The coordinate point G (3, -2)
Here, the x-coordinate of point F is 3 and the x-coordinate of point G is 3. They both are sam
The X-coordinate of point F is the same as the x-coordinate of Point G.
C. Draw a line segment that connects the two points. What is the distance between Point F and the point where the line intersects the x-axis?
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance
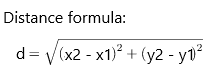
Line segment: A line segment has two definite endpoints in a line. The length of the line segment is fixed, which is the distance between two fixed points.
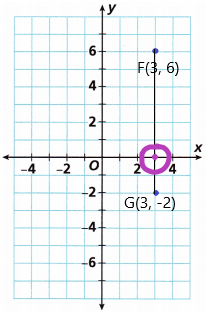
The point that intersects at X-axis is at 3.
D. What is the absolute value of the y-coordinate of point F?
Answer:
Absolute coordinates refer to a Cartesian System that uses an x-axis, y-axis, and sometimes z-axis to establish a point some distance from a common origin.
– The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.
The coordinate of point F is (3, 6)
According to the definition, the absolute value of the y-coordinate of point F is 6.
E. What is the distance between Point G and the x-axis? What is the absolute value of the y-coordinate of Point G?
Answer:
The distance between point G and the x-axis:
Given, P(3, -2) is a point at a distance from the origin.
The coordinates of a point at the origin will be (0,0).
Using the distance between the formula for two points, we know;
Here, x1 = 3, x2 = 0, y1 = -2, y2 = 0.
Thus, putting all the values of x and y in the formula, we get;
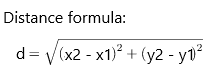
Absolute coordinates refer to a Cartesian System that uses an x-axis, y-axis, and sometimes z-axis to establish a point some distance from a common origin.
– The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.
The coordinate of point G is (3, -2)
According to the definition, the absolute value of the y-coordinate of point F is |-2| = 2.
F. What do you notice about the absolute value of each point’s y-coordinate and the distance of the point to the x-axis?
Answer:
The absolute value we got is 2.
The distance we got is 3.6
The difference between those values is 1.6
G. The points (are/aren’t) in the same quadrant.
Answer:
The absolute value we got is 2.
The distance we got is 3.6
both points are in the same quadrant. Because both the values are positive and lie in quadrant I.
H. Because the points are in different quadrants, add the absolute values of the points’ y-coordinates to find the distance between Points F and G.
![]() +
+ ![]() =
= ![]()
Answer:
The coordinate of point F is (3, 6)
The coordinate of point G is (3, -2)
The absolute value of the y-coordinate of point F is 6.
The absolute value of the y-coordinate of point G is -2.
The distance between points F and G:
d = 6 + (-2) = 6-2 = 4 units.
Turn and Talk Explain how you might find the distance between two points with the same x-coordinate that were both in Quadrant I.
Answer:
If the points lie in the same quadrant, subtract the absolute values of the appropriate coordinates.
For example, take the above-given quadrants:
The coordinate of point F is (3, 6)
The coordinate of point G is (3, -2)
use absolute value to find the distance:
|6| – |-2| = 8 units.
Question 3.
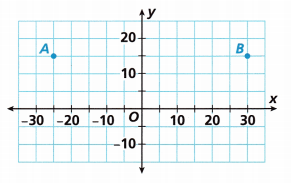
A wholesale chain has two stores as shown on the graph. Each unit represents 10 miles. How far apart are the stores?

A. What are the coordinates of each store?
Store A: (![]() ,
, ![]() ); Store B: (
); Store B: (![]() ,
, ![]() )
)
Answer:
The coordinates of store A: (-25, 15)
The coordinates of store B: (30, 15)
B. The y-coordinate of Store A is ____________ as the y-coordinate of Store B.
Answer:
The Y-coordinate of store A is the same as the Y-coordinate of store B.
Because in the given points Y-coordinates are the same.
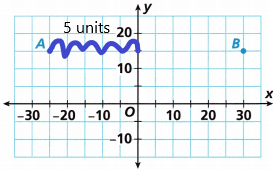
C. Find the distance between Store A and the y-axis using absolute value.
Distance: |![]() | =
| = ![]() units
units
Answer:
The coordinates of store A: (-25, 15)
The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.
The distance is |5| = 5 units.
D. Find the distance between Store B and the y-axis using absolute value.
Distance: |![]() | =
| = ![]() units
units
Answer:
The coordinates of store B: (30, 15)
The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.
The distance is |6| = 6 units.
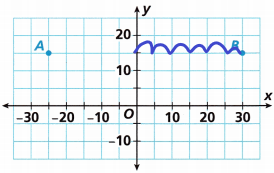
E. Find the distance, in miles, between the two stores.
Distance (units): ![]() +
+ ![]() =
= ![]() units
units
Distance (in miles): ![]() ×
× ![]() =
= ![]() units
units
Answer:
The coordinates of store A: (-25, 15)
The coordinates of store B: (30, 15)
The points are different quadrants with the same y-coordinates
Use the absolute value to find the distance.
|30 – (-25)| = 55 units
Distance in miles:
count the squares from store A to store B.
Each unit represents 10 miles.
the distance we got after counting the squares is 11 and we know each unit.
11 x 10 = 110 miles.
Turn and Talk How would you find the distance between two points in the same quadrant using absolute value? Explain.
Answer:
If the points lie in the same quadrant, subtract the absolute values of the appropriate coordinates.
Check Understanding
Question 1.
Amy is making a map. She wants to reflect Point (-6, 5) across the y-axis. What are the coordinates of its reflection?
Answer:
– a reflection is known as a flip. A reflection is a mirror image of the shape. An image will reflect through a line, known as the line of reflection.
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
The above-given point: (-6, 5)
Amy wants to reflect the point over the y-axis:
According to the above definition, the reflection will be:
The coordinates of its reflection is (6, 5)
Question 2.
Are the points P(80, -75) and Q(-35, -75) in the same quadrant or different quadrants? What is the distance between the points? Explain how you found the distance.
Answer:
The above-given coordinates:
P(80, -75); Q(-35, -75)
Both points are different quadrants.
The quadrants are different.
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
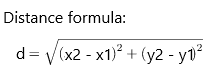
P = (x1, y1) = (80, -35)
Q = (x2, y2) = (-75, -75)
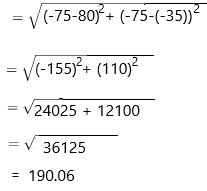
Question 3.
Are the points A(-4, -10) and B(-4, -2) in the same quadrant or different quadrants? What is the distance between the points? Explain how you found the distance.
Answer:
Both points are in the same quadrants.
The given points are:
A(-4, -10) and B(-4, -2)
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
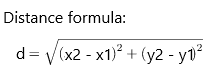
A = (-4, -4); B(-10, -2)
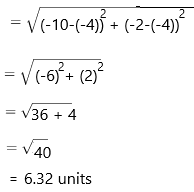
On Your Own
Question 4.
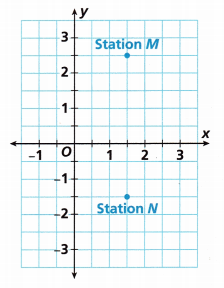
The positions of two neighbouring train stations are shown. Each unit on the coordinate plane is equal to 1 mile. How far apart are the two stations?

A. What are the coordinates of each station?
Station M: (![]() ,
, ![]() ); Station N: (
); Station N: (![]() ,
, ![]() )
)
Answer:
The coordinates of station M:(1.5, 2.5)
The coordinates of station N:(1.5, -1.5)
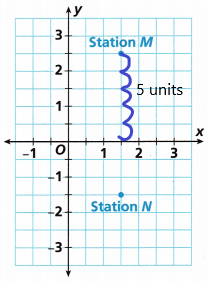
B. What is the distance in miles between Station M and the x-axis?
Answer:
The coordinates of station M:(1.5, 2.5)
The distance between station M and the x-axis is 5 units.
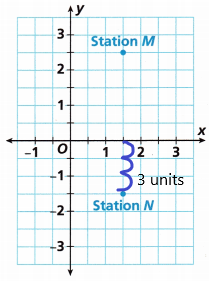
C. What is the distance in miles between Station N and the x-axis?
Answer:
The coordinates of station N:(1.5, -1.5)
The distance between station N and the x-axis is 3 units.
D. What is the distance in miles between the two stations?
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
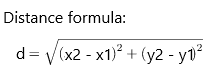
The coordinates of station M:(1.5, 2.5)
The coordinates of station N:(1.5, -1.5)
A = (x1, y1) = (1.5, 1.5)
B = (x2, y2) = (2.5, -1.5)
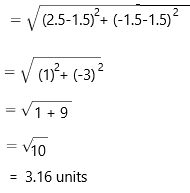
For Problems 5-8, use the coordinate plane.
Question 5.
Name two points that have the same y-coordinate.
Answer:
The two points that have the same y-coordinate is point Q and U
the point Q in the y-coordinate is -5.
the point U in the y-coordinate is -5.
Question 6.
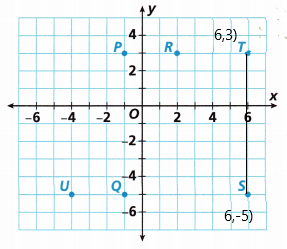
What ¡s the distance between Points S and T? Are they in the same quadrant?
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
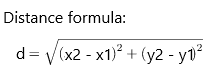
The coordinate of point S: (6, -5)
The coordinate of point T: (6, 3)
A = (x1, y1) = (6, 6)
B = (x2, y2) = (-5, 3)
The points S and T are different quadrants.
Question 7.
What is the distance between Points R and T? Are they ¡n the same quadrant?
Answer:
A distance on the coordinate plane can be found if we know the coordinates of the starting and ending points of that distance. Therefore, we can use the following steps to find distances on the coordinate plane:
Step 1: Determine the coordinates of the two given points on the plane. For example, we can have the points
A = (x1, y1) and B = (x2, y2).
Step 2: Apply the distance formula to find the distance between the given points.
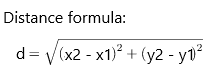
The coordinate of point R: (2, 3)
The coordinate of point T: (6, 3)
A = (x1, y1) = (2, 6)
B = (x2, y2) = (3, 3)
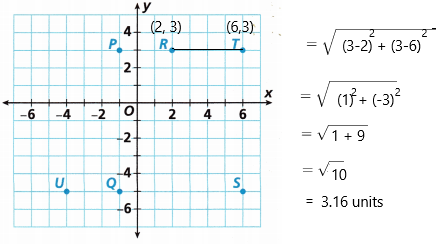
The points R and T are in the same quadrant.
Question 8.
What is the distance between Points 0 and U1 Are they in the same quadrant?
Answer:
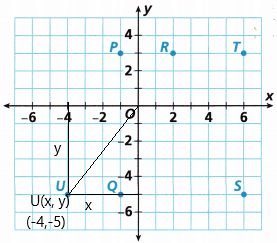
Let us calculate the distance between point U and the origin. U is x units away from the y-axis and y units away from the x-axis.
Therefore the distance between any point (x, y) in XY-plane and the origin (0, 0) is
![]()
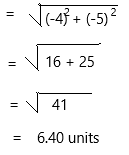
Question 9.
Critique Reasoning Theo says that the point (-5, 7) and its reflection are always 10 units apart. Is he correct? Explain.
Answer:
The above-given point: (-5, 7)
The reflection over x-axis: (-5, -7)
The reflection over the y-axis: (5, 7)
The reflection over the y-axis is 10 units apart.
The reflection over the x-axis is above 10 units apart.
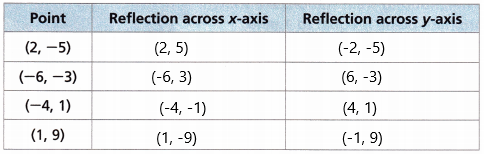
Question 10.
Use Repeated Reasoning Write the coordinates of each point after each reflection.
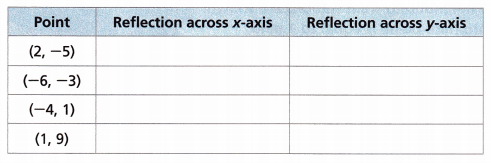
Answer:
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
According to the above rules, we can write the reflection of points. The table is filled and shown below:
Question 11.
The graph shows the positions of two movie theatres. Each unit of the coordinate plane represents 8 miles.
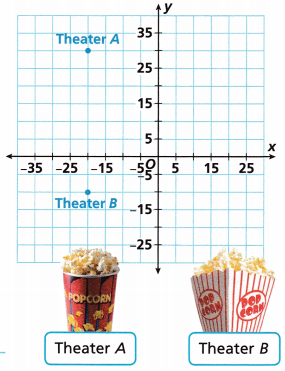
A. How far apart are the movie theatres in units of the coordinate plane?
Answer:
The coordinate points of theatre A (-20, 30)
The coordinate points of theatre B (-20, -10)
The points are in the different quadrants and have the same x-coordinates.
Use absolute value to find the distance.
distance = |30| – |-10|
distance = 40 units.
Therefore, the distance between the movie theatres is 40 units.
B. How far apart are the movie theatres in miles?
Answer:
– Count the squares between the theatres.
– The number of squares between theatre A and theatre B is 8.
– Already given that each unit is 8 miles.
– Now the distance is 8 x 8 = 64 units.
Question 12.
Use Structure Find the distance between Points B(-2, -8) and C(-2, 3) without graphing. How did you find the distance?
Answer:
The coordinate points are B(-2, -8) and C(-2, 3)
The points are different quadrants with the same x-coordinates. So we can use absolute values to find the distance.
|-8 – 3| = |-11|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 11.
Therefore, the distance is 11 units.
Question 13.
Use Structure Find the distance between points P(3, 9) and R(7, 9) without graphing. Why do you subtract instead of add to find the distance?
Answer:
The coordinate points are P(3, 9) and R(7, 9)
They are the same quadrants with the same y-coordinates.
Note: If points lie in the same quadrants, subtract the absolute values of the appropriate coordinates.
|7 – 3| = 4 units.
Therefore, the distance is 4 units
I’m in a Learning Mindset!
What is challenging about finding distance in a coordinate plane? Can I work through it on my own or do I need help?
Answer:
Lesson 11.3 More Practice/Homework
Question 1.
On the coordinate plane provided each unit represents 20 miles. Use the coordinate plane to find how far apart two airports are from each other.

A. Plot and label the points to represent the locations of Airport A(125, -325) and Airport B(125, 125). Then connect the points.
Answer:
The coordinate points of airport A(125, -325)
The coordinate points of airport B(125, 125)
Now plot the points in the coordinate plane and connect them.
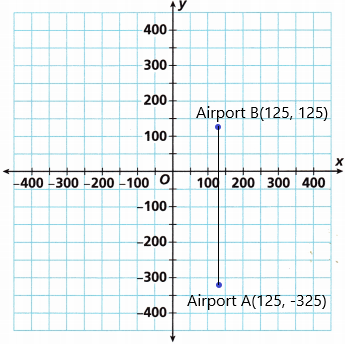
B. What is the distance between Airport A and the x-axis in units and in miles?
Answer:
The distance between airport A and the x-axis is 7 units.
count the square between airport A and the x-axis.
We know that each unit is 20 miles.
distance is 7 x 20 = 140 units.
C. What is the distance between Airport B and the x-axis in units and in miles?
Answer:
The distance between airport B and the x-axis is 3 units.
count the square between airport B and the x-axis.
We know that each unit is 20 miles.
distance is 3 x 20 = 60 units.
D. What is the distance between the two airports in miles?
Answer:
The coordinate points of airport A(125, -325)
The coordinate points of airport B(125, 125)
both points are different quadrants with the same x-coordinates then add the absolute values of appropriate coordinates.
We can use the absolute value to find the distance.
|125 – (-325)| = |450|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 450 units.
Therefore, the distance is 450 units.
Question 2.
What are the coordinates of Point Z(-3.9, -9.3) after a reflection across the y-axis?
Answer:
The above-given coordinate point Z is (-3.9, -9.3)
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
According to the above rules, we can write the reflection of points.
The point reflection over the Y-axis is (3.9, -9.3)
Math on the Spot For Problems 3-4, find the distance between the points.
Question 3.
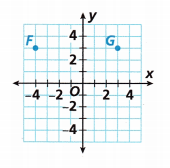
Answer:
The coordinate points of F are (-4, 3)
The coordinate points of G are (3, 3)
The quadrants are different with the same y-coordinates. So we can use absolute values to find the distance.
|-4| – |3| = |-4 – 3| = |-7|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 7 units.
Therefore, the distance is 7 units.
Question 4.
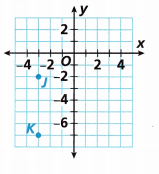
Answer:
The coordinate of point J is (-3, -2)
The coordinate points of K are (-3, -7)
the quadrants are the same with the same x-coordinates. So we can use the absolute values to find the distance.
|-7| – |-2| = |-7 + 2| = |-5|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 5 units.
Therefore, the distance is 5 units.
Question 5.
Use Structure Find the distance between Points D(-5, -3) and E(9, -3) without graphing. How did you find the distance?
Answer:
The coordinate points of D are (-5, -3)
The coordinate points of E are (9, -3)
The quadrants are different with the same y-axis. So we can use absolute values to find the distance.
|-5| – |9| = |-5 – 9| = |-14|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 14 units.
Therefore, the distance is 14 units. (or)
to find the distance between two points we can use the distance formula:
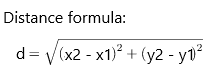
substitute the values and calculate.
Test Prep
Question 6.
What is the distance between the points (-2.5, 6.5) and (2.5, 6.5)?
__________ units
Answer:
The above-given coordinates are (-2.5, 6.5) and (2.5, 6.5)
The quadrants are different with the same y-coordinates. So we can use absolute values to find the distance.
|-2.5 – 2.5| = |-5|
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 5 units.
Therefore, the distance is 5 units.
Question 7.
What is the distance between the points (3, 4.1) and (3, 1.2)?
__________ units
Answer:
The above-given coordinates are (3, 4.1) and (3, 1.2)
The quadrants are different with the same x-coordinates. So we can use absolute values to find the distance.
|4.1 – 1.2| = 2.9
Note: If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
According to the above note, the value is 2.9 units.
Therefore, the distance is 2.9 units.
Question 8.
Which point is a reflection of (-3, 8) across the x-axis on a coordinate plane?
(A) (-8, 3)
(B) (-3, -8)
(C) (3, 8)
(D) (3, -8)
Answer: Option B is correct.
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
According to the above rule, we can write the reflection of points.
The point reflection over the x-axis is (-3, -8)
Question 9.
Which point is a reflection of (-5.2, 9.5) across the y-axis on a coordinate plane?
(A) (-5.2, -9.5)
(B) (5.2, 9.5)
(C) (5.2, -9.5)
(D) (9.5, -5.2)
Answer: Option B is correct.
– When a point is reflected across the Y-axis, the Y-coordinates remain the same. But the X-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the Y-axis is (-x, y).
– When a point is reflected across the X-axis, the x-coordinates remain the same. But the Y-coordinates are transformed into their opposite signs. Therefore, the reflection of the point (x, y) across the X-axis is (x, -y).
According to the above rules, we can write the reflection of points.
The point reflection over the Y-axis is (5.2, 9.5)
Spiral Review
Question 10.
A truck driver drives 245 miles and needs to drive m miles in all. Write an equation for the number of miles d the driver has left to drive.
Answer:
The number of miles a truck driver drives = 245
the number of miles needs to drive = m
We need to write the equation for the number of miles the driver has left to drive = d
The equation is:
m = 245 + d
Question 11.
Draw the polygon with vertices (3, -1), (3, 4), (-2, 4), and (-2, -1) on the coordinate plane. Classify the polygon.
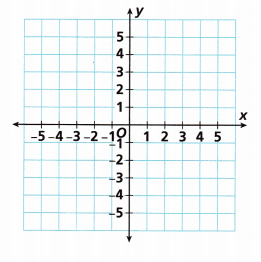
Answer:
The above-given vertices are: (3, -1), (3, 4), (-2, 4), and (-2, -1)
plot the vertices in the coordinate plane.
Connect the vertices.
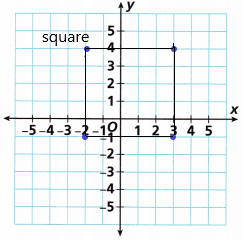
– After the vertices are connected in the coordinate plane, the polygon we got is square.