We included HMH Into Math Grade 6 Answer Key PDF Module 11 Lesson 1 Graph Rational Numbers on the Coordinate Plane to make students experts in learning maths.
HMH Into Math Grade 6 Module 11 Lesson 1 Answer Key Graph Rational Numbers on the Coordinate Plane
I Can identify and graph rational number ordered pairs in all four quadrants on a coordinate plane.
Spark Your Learning
The Robinsons’ family home is located at (3, 7) on the coordinate grid, where the units are miles. They begin their vacation by leaving home and driving to a restaurant located at (3, 1). From the restaurant, the family drives to a campground located 5 miles due west of the restaurant. After spending five days at the campground, the family drives 6 miles due south to visit their grandparents. What are the coordinates of the campground and their grandparents’ home? Explain how you found the coordinates of each location.

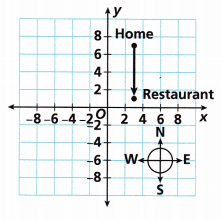
Answer:
According to the guidelines of the given question we have to place the points.
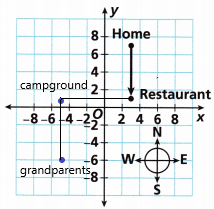
Turn and Talk Explain how the coordinate grid relates to the number lines you used in Module 1.
Answer:
Build Understanding
A coordinate plane is formed by the intersection of two number lines called axes. The horizontal number line is called the x-axis, and the vertical number line is called the y-axis. The origin is the point where the x-axis and y-axis intersect. Notice that the coordinate plane is divided into four regions called quadrants. Remember that an ordered pair is two numbers in the form (x, y) used to locate a point on a coordinate plane.
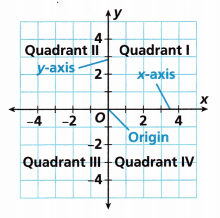
Question 1.
How do you identify the coordinates of a point on a coordinate plane?
A. The x-coordinate and the y-coordinate of an ordered pair in Quadrant I will both be positive numbers. What are the coordinates of Point A? How can you describe the location of Point A?
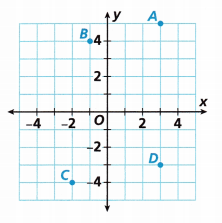
Answer:
Quadrant I: The first quadrant is available in the upper right-hand corner of the plane. Both x and y happen to consist of positive values in this quadrant.
The coordinates of points A are 3 and 5.
Point A described as (3, 5)
3 is the value of X.
5 is the value of Y.
B. Look at Quadrant II. What values can the x-coordinate of an ordered pair in this quadrant have? What values can the y-coordinate have?
Answer:
Quadrant II: The second quadrant happens to be in the upper left-hand corner of the plane. Moreover, X has negative values in this quadrant and y has positive values.
The ordered pairs can be (-2, 2) and (-4, 4)
-2 is the value of X
2 is the value of Y.
C. Look at Quadrant III. What values can the x-coordinate of an ordered pair in this quadrant have? What values can the y-coordinate have?
Answer:
Quadrant III: The third quadrant is in the bottom left corner of the plane. Furthermore, both x and y have negative values in this quadrant.
The ordered pair (-2, -2) and (-4, -4)
-2 is the value of X
-2 is the value of Y
Likewise, -4 is the value of X
-4 is the value of Y
D. Look at Quadrant IV. What values can the x-coordinate of an ordered pair in this quadrant have? What values can the y-coordinate have?
Answer:
Quadrant IV: The fourth quadrant is in the bottom right corner of the plane. In this coordinate X has positive values and y has negative values.
The ordered pair (2, -2) and (4, -4)
2 is the value of X
-2 is the value of Y
likewise, 4 is the value of X
-4 is the value of Y.
E. What are the coordinates of Points B, C, and D?
Answer:
The coordinate points of B are (-1, 4)
The coordinate points of C are (-2, -4)
The coordinate points of D are (3, -3)
Turn and Talk Suppose one number in an ordered pair is zero. Is it possible to graph that point? Explain.
Answer:
Yes, we can graph that point.
The above-given question is one number in an ordered pair is zero.
Suppose if we take the ordered pair (0, 4). So we can plot the point in the coordinate plane.
Step It Out
Question 2.
A city mayor wants to build a fence around a community garden. The fence will be in the shape of a rectangle. Three fence posts are placed at Points A, B, and C, which are corners of the rectangle. The fourth fence post will be placed at Point D, which is not shown.

A. What are the coordinates of Points A, B, and C?
A(![]() ,
, ![]() ), B(
), B(![]() ,
, ![]() ), C(
), C(![]() ,
, ![]() )
)
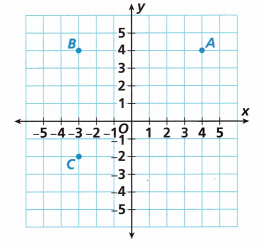
Answer:
the coordinate points of A are (4, 4)
The coordinate point of B are (-3, 4)
The coordinate points of C are (-3, -2)
B. To complete the rectangle, which quadrant must Point D be in?
Answer:
To complete the rectangle, we must point D in quadrant IV.
C. What are the coordinates of point D?
D(![]() ,
, ![]() )
)
Answer:
the coordinates of point D are (4, -2)
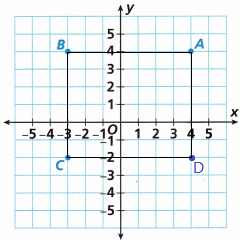
D. Graph Point D on the coordinate plane shown. Then connect the points to form the rectangle.
Answer:
To form a rectangle with the points and the graph is shown below.
Question 3.
Coordinates for points graphed on a coordinate plane can rational number, including decimals.
A. The interval for the x- and y-axes is __________ on the coordinate plane shown.
Answer:
perpendicular
The x-axis and y-axis are axes in the Cartesian coordinate system. Together, they form a coordinate plane. The x-axis is usually the horizontal axis, while the y-axis is the vertical axis. They are represented by two number lines that intersect perpendicularly at the origin, located at (0, 0),
B. Graph the ordered pairs on the coordinate plane shown.
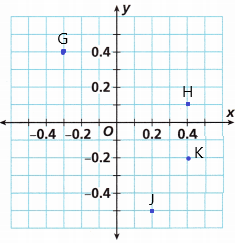
G(-0.3, 0.4), H(0.4, 0.1), J(0.2, -0.5)
Answer:
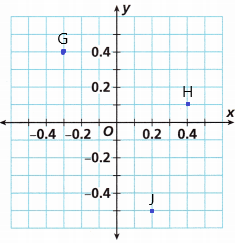
C. In which quadrant is Point G located?
Answer:
The above-given coordinate of point G (-0.3, 0.4)
It was located in quadrant II. Because In the second quadrant, we have a negative x-axis and a positive y-axis. In this quadrant, the x value will be negative and the Y-value will be positive. In this quadrant, the angle measures from 90 degrees to 180 degrees.
D. In which quadrant is Point H located?
Answer:
The above-given coordinate of point H (0.4, 0.1)
It was located in quadrant I. Because In the first quadrant, we have a positive x-axis and positive y-axis. x and y both values are positive in this quadrant. In this quadrant, the angle measure starts from 0 degrees to 90 degrees. It is in the shape of a right angle.
E. In which quadrant is Point J located?
Answer:
The above-given coordinate of point J (0.2, -0.5)
It was located in quadrant IV. Because In this quadrant, we have a positive x-axis and a negative y-axis. The x value is positive and the value is negative in this quadrant. The angle measures from 270 degrees to 360 degrees.
F. Plot a new Point K in Quadrant IV and write the point’s coordinates.
Answer:
For suppose if we plot a new point that would be named K.
The assumed coordinate point is (0.4, -0.2)
Turn and Talk Explain why the ordered pair (-0.4, -0.5) represents a different location than the ordered pair (0.4, 0.5).
Answer:
The ordered pair (-0.4, -0.5) and (0.4, 0.5) are represented in a different locations because according to the quadrants the ordered pairs must locate in the coordinate plane.
The ordered pair (-0.4, -0.5) are having negative signs so it could be located in quadrant III.
The ordered pair (0.4, 0.5) are having positive signs so it could be located in quadrant I.
Question 4.
Coordinates for points graphed on a coordinate plane can be any rational number, including fractions.
A. The interval for the x- and y-axes is __________ on the coordinate plane.
Answer: perpendicular
The x-axis and y-axis are axes in the Cartesian coordinate system. Together, they form a coordinate plane. The x-axis is usually the horizontal axis, while the y-axis is the vertical axis. They are represented by two number lines that intersect perpendicularly at the origin, located at (0, 0),
B. Graph the points with fractional coordinates.
P(1\(\frac{1}{2}\), –\(\frac{3}{4}\)), Q(-1\(\frac{1}{4}\), -1), R(-\(\frac{1}{2}\), 1\(\frac{1}{4}\))
Answer:
The point P ( 1 1/2, -3/4). It is located in quadrant IV.
The point Q (-1 1/4, -1). It is located in quadrant III.
The point R (-1/2, 1 1/4). It is located in quadrant II.
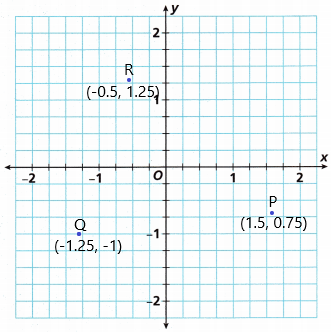
C. Determine the quadrant in which each point is located.
Point P ____________
Point Q ____________
Point R ____________
Answer:
Point P is located in quadrant IV because the X-coordinate is positive and the Y-coordinate is negative.
Point Q is located in quadrant III because both the coordinates are negative.
Point R is located in quadrant II because the X-coordinate is negative and the Y-coordinate is positive.
Check Understanding
Question 1.
A grocery store is located at (-5, -4) on a coordinate plane. Shawn says it is located in Quadrant IV. Wren says it is located in Quadrant III. Who is correct? Explain why.
Answer:
Wren is correct because it is located in quadrant III. Because both the signs are negative.
In the third quadrant, we have a negative x-axis and a negative y-axis. Both x and y values in this quadrant are negative. The angle measures from 180 degrees to 270 degrees in this quadrant.
Question 2.
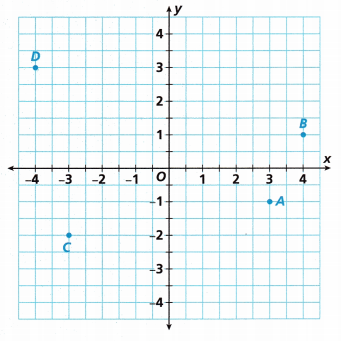
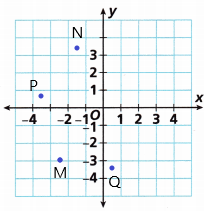
Identify the quadrant in which each point is located in the coordinate plane shown.
Point A ____________
Point B ____________
Point C ____________
Point D ____________
Answer:
The point A in the above-given graph shows that the coordinate points.
The coordinate points of A are (3, -1)
The coordinate points of B are (4, 1)
The coordinate points of C are (-3, -2)
The coordinate points of D are (-4, 3)
Question 3.
Graph and label the points on the coordinate plane shown.
M(-2\(\frac{1}{2}\), -3), N(-1.5, 3.5), P(-3\(\frac{1}{2}\), \(\frac{3}{4}\)). Q(0.5. -3.5), R(2\(\frac{3}{4}\), -1\(\frac{1}{2}\))
Answer:
-2\(\frac{1}{2}\), -3 can be written as -2 1/2
The coordinates of M are (-2 1/2, -3)
The coordinates of N are (-1.5, 3.5)
The coordinates of P are (-3 1/2, 3/4)
The coordinates of Q are (0.5, -3.5)
The coordinates of M:
The coordinates should be placed in quadrant III because both the signs are negative.
The coordinates of N:
The coordinates should be placed in quadrant II because the X-coordinate is negative and the Y-coordinate is positive.
The coordinates of P:
The coordinates should be placed in quadrant II because the X-coordinate is negative and the Y-coordinate is positive.
The coordinates of Q:
The coordinates should be placed in quadrant IV because the X-coordinate is positive and the y-coordinate is negative.
On Your Own
Question 4.
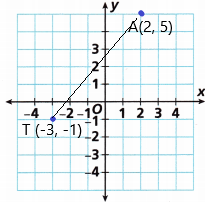
Terrell’s house is plotted on a coordinate plane at (-3, -1).
A. In which quadrant is Terrell’s house located?
Answer:
The above-given coordinates are (-3, -1)
The lower left-hand corner of the graph is the third quadrant. It contains the negative values of both x and y.
B. To get to Annie’s house from Terrell’s house, you have to move 5 units directly north and 2 units directly east. In which quadrant is Annie’s house?
Answer:
5 units north means the y-coordinate is 5. And then 2 units directly east means the x-coordinate is 2
Annie’s house is in the first quadrant.
Therefore, the coordinates are (2, 5)
both the signs are positive.
In the first quadrant, we have a positive x-axis and positive y-axis. x and y both values are positive in this quadrant. In this quadrant, the angle measure starts from 0 degrees to 90 degrees. It is in the shape of a right angle.
C. What are the coordinates of Annie’s house?
Answer:
the coordinates are (2, 5)
both the signs are positive.
In the first quadrant, we have a positive x-axis and a positive y-axis. x and y both values are positive in this quadrant. In this quadrant, the angle measure starts from 0 degrees to 90 degrees. It is in the shape of a right angle.
D. Graph the locations of Terrell’s house, Point T, and Annie’s house, Point A, on the coordinate plane.

Answer:
The Terrell’s house coordinate points are (-3, -1)
The Annie’s house coordinate points are (2, 5)
The graph is shown below:
Question 5.
Attend to Precision Alex is making a blueprint of Kite QRST on a coordinate plane. Each corner of the kite will lie directly on the x- or y-axis. The top of the kite, Point Q, is at (0, 2.5). The left corner, Point R, is at (-3.5, 0). The kite is 7 units from bottom to top and 7 units across from left to right. What are the coordinates of Points S and T? Explain how you know. Then draw and label the kite on the coordinate plane shown.
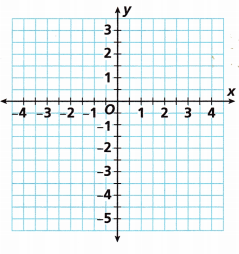
Answer:
The 7 units from bottom to top means count from -5, -4, -3, -2, -1, 0, 1.
The 7th unit is one.
The coordinates are S (0, 1)
The 7 units from left to right means it starts from -4, -3, -2, -1, 0, 1, 2
The 7th unit is 2
The coordinates are T (0, 2)
Question 6.
In which quadrant is the point (\(\frac{13}{48}\), –\(\frac{1}{16}\)) located?
Answer:
\(\frac{13}{48}\) can be written as 13/48
–\(\frac{1}{16}\) can be written as – 1/16
This both are 13/48 is X value and -1/16 is Y value.
(+, -) are the 4th quadrants.
So, we can locate them in quadrant IV.
The fourth quadrant is in the bottom right corner of the plane. In this coordinate X has positive values and y has negative values.
Question 7.
In which quadrant is the point (-1.7, 4.9) located?
Answer:
– In the second quadrant, we have a negative x-axis and a positive y-axis. In this quadrant, the x value will be negative and the Y value will be positive. In this quadrant, the angle measures from 90 degrees to 180 degrees.
If x < 0, y >0, then the point is in quadrant II
The coordinates are (-1.7, 4.9)
In quadrant II we locate this coordinate.
Question 8.
Open-Ended Name the coordinates of one point in Quadrant I, one point in Quadrant II, one point in Quadrant III, and one point in Quadrant IV.
Answer:
– In the first quadrant, we have a positive x-axis and a positive y-axis. x and y both values are positive in this quadrant. In this quadrant, the angle measure starts from 0 degrees to 90 degrees. It is in the shape of a right angle.
If both x, y > 0, then the point is in quadrant I
The coordinates are ( 1, 4)
– In the second quadrant, we have a negative x-axis and a positive y-axis. In this quadrant, the x value will be negative and the Y value will be positive. In this quadrant, the angle measures from 90 degrees to 180 degrees.
If x < 0, y >0, then the point is in quadrant II
The coordinates are (-1, 4)
– In the third quadrant, we have a negative x-axis and a negative y-axis. Both x and y values in this quadrant are negative. The angle measures from 180 degrees to 270 degrees in this quadrant.
If x < 0, y < 0, then the point lies in quadrant III
The coordinates are (-1, -4)
– In this quadrant, we have a positive x-axis and a negative y-axis. The x value is positive and the value is negative in this quadrant. The angle measures from 270 degrees to 360 degrees.
If x > 0, y <0= 0, then point goes to quadrant IV
The coordinates are (1, -4)
Question 9.
Use Structure An ordered pair with a negative x-coordinate and a negative y-coordinate is in which quadrant?
Answer:
If both coordinates are negative then they are quadrant III.
In the third quadrant, we have a negative x-axis and a negative y-axis. Both x and y values in this quadrant are negative. The angle measures from 180 degrees to 270 degrees in this quadrant.
Question 10.
The ordered pair (4, -8) is in Quadrant __________. If the coordinates are switched so that it is (-8, 4), it will now be in Quadrant __________.
Answer:
The above-given ordered pair (4, -8).
Now observe the signs. The signs are (+, -) so the ordered pair is in quadrant IV.
If they were (-8, 4) then again observe the signs. The signs are (-, +) so the ordered pair is in quadrant II.
Question 11.
Tamara designs video games. She uses a coordinate plane to plot the moves of a character in the game. The character begins at the origin. Use the coordinate plane to find the character’s position.

A. The character moves 3 units left and 2 units down. What are the coordinates of the character after this move? In which quadrant is the character located?
Answer:
In the coordinate plane left means, all the numbers are negative.
3 units left means it will be -3.
and from their 2 units down means, we get -2.
The coordinates are (-3, -2)
It was quadrant III because both the signs are negative.
B. The character then moves 6 units right and 6 units down. What are the coordinates of the character now? In which quadrant is the character located now?
Answer:
In the coordinate plane right means, the plane has all positive numbers.
In the above-given, that character will move 6 units right so the value of X is 6 and from their 6 units down it will move so definitely, it will be -6.
The coordinates are (6, -6)
It was quadrant IV because the signs are (+, -)
C. What move could the character make to return to the origin? Explain.
Answer:
The moves from the right or left we move from the centre. The centre point is the origin.
Both the points were made at the centre.
The coordinates are (0, 0)
D. Draw the path of the character on the coordinate plane, using A and 6 to label the places where the character stopped.
Answer:
Question 12.
Open-Ended Name the coordinates of two points so that the line segment drawn from one to the other will intersect the y-axis.
Answer:
I’m in a Learning Mindset!
What is challenging about graphing rational numbers on the coordinate plane? Can I work through it on my own, or do I need help?
Answer:
Lesson 11.1 More Practice/Homework
Question 1.
Graph each of the following ordered pairs on the coordinate plane and name the quadrant in which they are located.
(2, 1), Quadrant __________
(-2, 1), Quadrant _________
(-2, -1), Quadrant _________
(2, -1), Quadrant _________
What shape can you make by connecting the four points?
Answer:
The coordinates (2, 1) come under quadrant I.
The coordinates (-2, 1) come under quadrant II.
The coordinates ( -2, -1) come under quadrant III.
The coordinates (2, -1) come under quadrant IV.
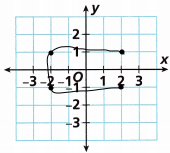
Question 2.
STEM A constellation is a group of stars that form a noticeable pattern in the night sky. It is often named after its form or identified with a mythological figure.

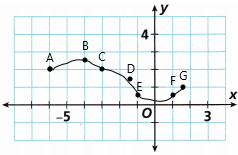
A. Graph each point. Then connect the points in alphabetical order to form a constellation.
A (-6, 2)
B (-4, 2.5)
C (-3, 2)
D (-1.5, 1.5)
E (-1, 0.5)
F (1, 0.5)
G (1.5, 2)
Answer:
The graph is drawn below and the points are connected in alphabetical order.
B. Which constellation do the points resemble the Big Dipper or the Little Dipper?
Answer: Big dipper
Explanation:
– the big dipper constellation is formed of seven stars
– We had connected 7 points in the above graph and moreover, the shape of the constellation is like a wheelbarrow or like a big ladle.
Question 3.
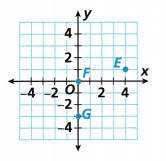
Math on the Spot Give the coordinates of each point on the coordinate plane shown.
E(![]() ,
, ![]() ), F(
), F(![]() ,
, ![]() ), G(
), G(![]() ,
, ![]() )
)
Answer:
– The point E is in quadrant I so definitely, the signs should be (+, +)
The coordinates of E are (4, 1)
– The point F is placed in the origin. So the value of X and Y is 0.
The coordinates of F are (0, 0)
– Point G is placed in quadrant IV. So definitely, the signs should be (+, -)
The coordinates of G are (0, 3)
Therefore, E (4,1); F (0, 0); G (0, 3).
Question 4.
In which quadrant is the point (-4\(\frac{1}{8}\), –\(\frac{5}{8}\)) located?
Answer:
-4\(\frac{1}{8}\) can be written as -4 1/8
–\(\frac{5}{8}\) can be written as -5/8
The coordinates are (-4 1/8, -5/8)
Both the signs are negative so the coordinates come under quadrant III.
Test Prep
Question 5.
Which ordered pairs are in Quadrant IV? Select all that apply.
(A) (-3.7, 4.1)
(B) (2\(\frac{2}{5}\), –\(\frac{24}{75}\))
(C) (5.11, 4.1)
(D) (6.3, -17.25)
(E) (-33, -42)
(F) (0.1, -0.25)
Answer: Options B, D, and F are correct.
Quadrant IV: The fourth quadrant is in the bottom right corner of the plane. In this coordinate X has positive values and y has negative values.
So, all the options who are having x have positive values and y has negative values are correct.

Question 6.
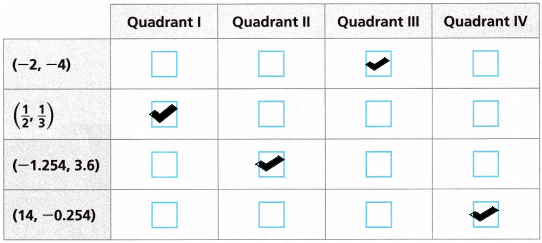
Match the ordered pair with the quadrant by filling in the correct boxes in the table.

Answer:
According to the signs, we can represent the quadrants.
– The coordinate (-2, -4) comes under quadrant III. Because both the signs are negative.
– The coordinate (1/2, 1/3) comes under quadrant I. Because both the signs are positive.
– The coordinate (-1.254, 3.6) comes under quadrant II. Because the value of the X-axis is negative and the value of the Y-axis is positive.
– The coordinate (14, -0.254) comes under quadrant IV. Because the value of the X-axis is positive and the value of the Y-axis is negative.
Question 7.
Draw a line to match each label to the correct
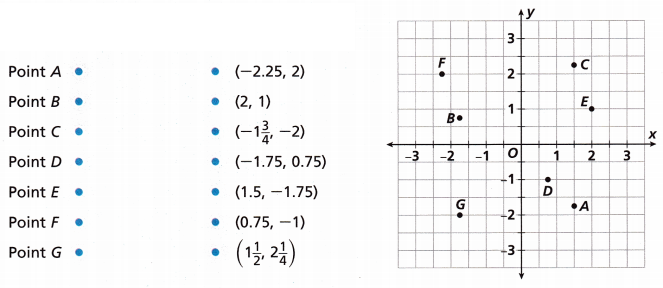
Answer:
– We need to represent the correct coordinates based on the given points in the graph.
– According to the X and Y-axis and based on the points A, B, C, D, E, F and G we need to match the correct coordinates.
– The point A is in quadrant IV so the signs are (+, -) and the coordinates of A are (1.5, -1.75)
– The point B is in quadrant II so the signs are (-, +) and the coordinates of B are (-1.75, 0.75)
– The point C is in quadrant I so the signs are (+, +) and the coordinates of C are (1 1/2, 2 1/4). These are in mixed fractions. We can convert them into improper fractions and then decimals. ( 3/2, 9/4) which is nothing but
( 1.5, 2.25).
– The point D is in quadrant IV so the signs are (+, -) and the coordinates are (0.75, -1)
– The point E is in quadrant I so the signs are (+, +) and the coordinates are (2, 1)
– The point F is in quadrant II so the signs are (-, +) and the coordinates are (-2.25, 2)
– The point G is in quadrant III so the signs are (-, -) and the coordinates are (-1 3/4, -2)
Spiral Review
Question 8.
Plot the points on the number line. 2.1, -0.4, 1.3, -1.8

Answer:
A number line is a pictorial representation of numbers on a straight line. It’s a reference for comparing and ordering numbers.
Let’s assume the given points be A, B, C, and D.
– Now mark the points in the number line.

– We have been given four numbers marked as A, B, C and D on a number line and we need to find out which decimal numbers they represent. Let us mark them one by one.
– We will start with completing the marking of the lines that have not been marked on the given number line. It can be clearly seen that there are 10 lines between two whole numbers on the number line. This means that the lines represent one-tenth of the number in the decimal form.
– Therefore, the lines between 2 and 3 will be marked as 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3.0. Similarly, we count for the second point from 0 to -1 will be marked as -0.1, -0.2, -0.3, -0.4, -0.5, -0.6, -0.7, -0.8, -0.9, -1.0. Likewise, we have to mark all the points.
Now, we shall check the position of the four points on this number line.
We can see that from the number line above, point A lies on the decimal number 2.1. Hence A = 2.1
Now, let us check the position of point B.
We can see that from the number line above, point B lies on the decimal number -0.4. Hence B = -0.4
Now, let us check the position of point C.
We can see that from the number line above, point C lies on the decimal number 1.3. Hence C = 1.3
Now, let us check the position of point D.
We can see that from the number line above, point D lies on the decimal number -1.8. Hence D = -1.8

Question 9.
In order to ride a roller coaster at Amazing Rides Fair, a person must be at least 42 inches tall. Write an inequality to express this situation.
Answer:
h≥48 inches tall
Explanation:
In order to ride on the ride, an individual must be at least 48 inches tall.
That means that the individual must be equal to 48 inches tall
h=48
and there might be a chance of the individual could be greater than 48 inches tall
h>48
So the individual could be greater than and equal to 48 inches tall
h≥48.