We included HMH Into Math Grade 6 Answer Key PDF Module 10 Real-World Relationships Between Variables to make students experts in learning maths.
HMH Into Math Grade 6 Module 10 Answer Key Real-World Relationships Between Variables
Which Relationship Does NOT Belong?
Describe the pattern shown by each relationship.
A.
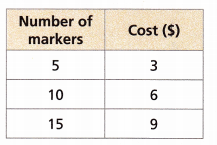
Answer:
– The package of 5 markers costs $3
– The package of 10 markers costs $6
– The package of 15 markers costs $9
In the column of a number of markers, the number is increased by adding 5 to the next number.
5 + 5 = 10; 10 +5 = 15;
In the cost column, the cost is increased by adding 3 to the next number.
3 + 3 = 6; 6 + 3 = 9.
B.

Answer:
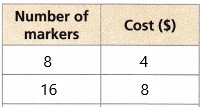
In the column of a number of markers, the number is increased by multiplying 2.
8 x 2 = 16
In the cost column, the cost is increased by multiplying 2
4 x 2 = 8
C.
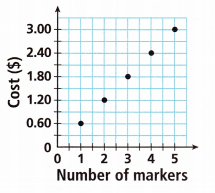
Answer:
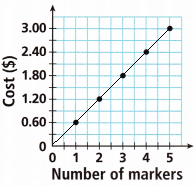
It is a perfect positive correlation.
– A scatter diagram is used to examine the relationship between both the axes (X and Y) with one variable. In the graph, if the variables are correlated, then the point drops along a curve or line. A scatter diagram or scatter plot gives an idea of the nature of the relationship.
– In a scatter correlation diagram, if all the points stretch in one line, then the correlation is perfect and is in unity.
D.

Answer:
The pack of 6 markers costs $3.60
The pack of 12 markers costs $7.20
In the column of a number of markers, the number is increased by multiplying 2.
6 x 2 = 12
In the cost column, the cost is increased by multiplying 2
3.60 x 2 = 7.20
Turn and Talk
Question 1.
Which relationship does not belong? Explain why.
Answer:
The scatter diagrams do not belong to the relationship.
The Scatter diagram method is a simple representation that is popularly used in commerce and statistics to find the correlation between two variables. These two variables are plotted along the X and Y axis on a two-dimensional graph and the pattern represents the association between these given variables.
Question 2.
Which relationship represents the best deal? Explain your reasoning.
Answer:
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Generate Patterns and Find Relationships
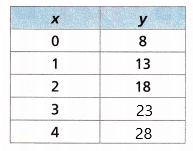
Describe a pattern you see in each table. Use the pattern to complete each table.
Question 1.
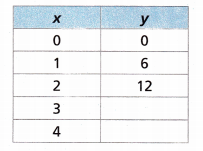
Answer:
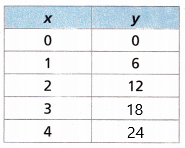
In the X column and Y column, the number is increased by multiplying 6.
0 x 6 = 0; 1 x 6 = 6; 2 x 6 = 12; 3 x 6 = 18; 4 x 6 = 24
Therefore, the filled table can be shown below:
Question 2.
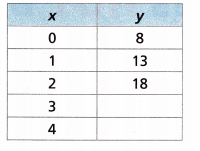
Answer:
In the x column, the number is increased by adding 1
0 + 1 = 1; 1 +1 = 2; 2 + 1 = 3; 3 + 1 = 4
In the Y column, the number is increased by adding 5
8 + 5 = 13; 13 + 5 =18; 18 + 5 = 23; 23 + 5 = 28
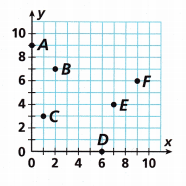
Identify Points on a Coordinate Grid.
Write the ordered pair for each point.
Question 3.
A _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of point A is (0, 9)
Question 4.
B _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of point B is (2, 7)
Question 5.
C _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of C is (1, 3)
Question 6.
D _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of D is (6, 1)
Question 7.
E _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of E is (7, 4)
Question 8.
F _______________
Answer:
Ordered pairs are usually used in coordinate geometry to represent a point on a coordinate plane. Also, they are used to represent elements of a relation.
– An ordered pair is a pair formed by two elements that are separated by a comma and written inside the parentheses. For example, (x, y) represents an ordered pair, where ‘x’ is called the first element and ‘y’ is called the second element of the ordered pair.
The ordered pair of F is (9, 6)
Graph and label each ordered pair on the coordinate grid.
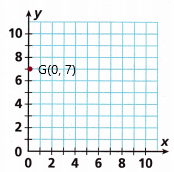
Question 9.
G(0, 7)
Answer:
The following are simple and easy steps to locate a point in a cartesian plane. Check out the guidelines, terms, and conditions to plot ordered pairs.
– Let us take one ordered pair.
– Get the sign of the x coordinate, and y coordinate of the ordered pair.
– Based on those signs, identify which quadrant the ordered pair belongs to.
– Count the x coordinate value on the x-axis starting from the origin.
– Similarly, count the y coordinate value on the y-axis from the origin.
– Mark the obtained point as the ordered pair.
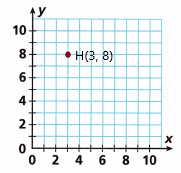
Question 10.
H(3, 8)
Answer:
The following are simple and easy steps to locate a point in a cartesian plane. Check out the guidelines, terms, and conditions to plot ordered pairs.
– Let us take one ordered pair.
– Get the sign of the x coordinate, and y coordinate of the ordered pair.
– Based on those signs, identify which quadrant the ordered pair belongs to.
– Count the x coordinate value on the x-axis starting from the origin.
– Similarly, count the y coordinate value on the y-axis from the origin.
– Mark the obtained point as the ordered pair.
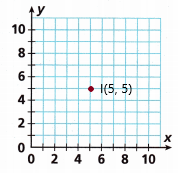
Question 11.
I(5, 5)
Answer:
The following are simple and easy steps to locate a point in a cartesian plane. Check out the guidelines, terms, and conditions to plot ordered pairs.
– Let us take one ordered pair.
– Get the sign of the x coordinate, and y coordinate of the ordered pair.
– Based on those signs, identify which quadrant the ordered pair belongs to.
– Count the x coordinate value on the x-axis starting from the origin.
– Similarly, count the y coordinate value on the y-axis from the origin.
– Mark the obtained point as the ordered pair.
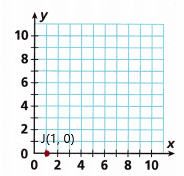
Question 12.
J(1, 0)
Answer:
The following are simple and easy steps to locate a point in a cartesian plane. Check out the guidelines, terms, and conditions to plot ordered pairs.
– Let us take one ordered pair.
– Get the sign of the x coordinate, and y coordinate of the ordered pair.
– Based on those signs, identify which quadrant the ordered pair belongs to.
– Count the x coordinate value on the x-axis starting from the origin.
– Similarly, count the y coordinate value on the y-axis from the origin.
– Mark the obtained point as the ordered pair.