We included HMH Into Math Grade 5 Answer Key PDF Module 9 Review to make students experts in learning maths.
HMH Into Math Grade 5 Module 9 Review Answer Key
Concepts and Skills
Question 1.
What is the area of a rectangular rug with side lengths 2\(\frac{1}{2}\) feet and 1\(\frac{1}{2}\) feet? Use the grid to find the area. Let each square represent \(\frac{1}{2}\) foot by \(\frac{1}{2}\) foot.
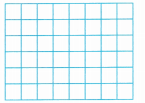
Answer:
The area is 3\(\frac{3}{4}\).
Explanation:
Given that the side lengths are 2\(\frac{1}{2}\) feet and 1\(\frac{1}{2}\) feet. So the area of the rectangular rug is 2\(\frac{1}{2}\) × 1\(\frac{1}{2}\) which is
= \(\frac{5}{2}\) × \(\frac{3}{2}\)
= \(\frac{15}{4}\)
= 3\(\frac{3}{4}\).
Question 2.
A closet measures 6\(\frac{1}{4}\) feet by 3\(\frac{1}{2}\) feet. How much carpeting is needed to cover the floor of the closet? Use the rectangle to draw an area model to solve.

Answer:
The area of the rectangle is 21\(\frac{7}{8}\) sq ft.
Explanation:
Given that a closet measures 6\(\frac{1}{4}\) feet by 3\(\frac{1}{2}\) feet. So the area will be 6\(\frac{1}{4}\) × 3\(\frac{1}{2}\) which is
= \(\frac{25}{4}\) × \(\frac{7}{2}\)
= \(\frac{175}{8}\)
= 21\(\frac{7}{8}\) sq ft.
Question 3.
Use Tools Michael has a piece of wood that is 2\(\frac{1}{4}\) feet long. He needs a second piece of wood that is 1\(\frac{1}{2}\) times as long as the first piece. How long is the second piece of wood? Tell what strategy or tool you will use to answer the question, explain your choice, and then find the answer.
A. 2\(\frac{1}{8}\) feet
B. 3\(\frac{3}{8}\) feet
C. 3\(\frac{5}{8}\) feet
D. 3\(\frac{3}{4}\) feet
Answer:
D.
Explanation:
Given that Michael has a piece of wood that is 2\(\frac{1}{4}\) feet long and he needs a second piece of wood that is 1\(\frac{1}{2}\) times as long as the first piece. So the second piece will be 2\(\frac{1}{4}\) + 1\(\frac{1}{2}\) which is
= \(\frac{9}{4}\) + \(\frac{3}{2}\)
= \(\frac{9+6}{4}\)
= \(\frac{15}{4}\)
= 3\(\frac{3}{4}\) ft.
Question 4.
Select all the expressions that are equivalent to 4\(\frac{4}{5}\).
A. 3 × 1\(\frac{3}{5}\)
B. 5 × 1\(\frac{2}{5}\)
C. 4 × 1\(\frac{1}{5}\)
D. 4 × 4 ÷ 5
E. 8 × 3 ÷ 5
Answer:
Explanation:
The expressions that are equivalent to 4\(\frac{4}{5}\) is 3 × 1\(\frac{3}{5}\) and 4 × 1\(\frac{1}{5}\). As
3 × 1\(\frac{3}{5}\) = 3 × \(\frac{8}{5}\)
= \(\frac{24}{5}\) which is 4\(\frac{4}{5}\).
4 × 1\(\frac{1}{5}\) = 4 × \(\frac{6}{5}\)
= \(\frac{24}{5}\).
Question 5.
The distance from the campground to the lake is 6\(\frac{3}{4}\) miles. If Anya has hiked \(\frac{2}{3}\) of the way from the campground to the lake, how far is she from the lake?
Answer:
The remaining distance is 6\(\frac{1}{12}\) miles.
Explanation:
Given the distance from the campground to the lake is 6\(\frac{3}{4}\) miles and if Anya has hiked \(\frac{2}{3}\) of the way from the campground to the lake. So the remaining distance is 6\(\frac{3}{4}\) – \(\frac{2}{3}\) which is
= \(\frac{27}{4}\) – \(\frac{2}{3}\)
= \(\frac{73}{12}\)
= 6\(\frac{1}{12}\) miles.
Question 6.
Miguel spends 3\(\frac{1}{2}\) hours working outside. He spends \(\frac{3}{4}\) of the time working in the garden. How much time does he spend working in the garden? Write an equation to model the problem.
Answer:
The time spend working in the garden is 4\(\frac{1}{4}\).
Explanation:
Given that Miguel spends 3\(\frac{1}{2}\) hours working outside and he spends \(\frac{3}{4}\) of the time working in the garden. So the time spend working in the garden is 3\(\frac{1}{2}\) + \(\frac{3}{4}\) which is
= \(\frac{7}{2}\) + \(\frac{3}{4}\)
= \(\frac{28+6}{8}\)
= \(\frac{34}{8}\)
= 4\(\frac{2}{8}\)
= 4\(\frac{1}{4}\).
Question 7.
A closet floor measures 2\(\frac{1}{2}\) feet by 5\(\frac{1}{2}\) feet. What is the area of the closet floor?
A. 10\(\frac{1}{4}\) square feet
B. 13\(\frac{1}{2}\) square feet
C. 13\(\frac{3}{4}\) square feet
D. 27\(\frac{1}{2}\) square feet
Answer:
13\(\frac{3}{4}\) square feet.
Explanation:
Given that a closet floor measures 2\(\frac{1}{2}\) feet by 5\(\frac{1}{2}\) feet. So the area of the closet floor is 2\(\frac{1}{2}\) × 5\(\frac{1}{2}\) which is
= 2\(\frac{1}{2}\) × 5\(\frac{1}{2}\)
= \(\frac{5}{2}\) × \(\frac{11}{2}\)
= \(\frac{55}{4}\)
= 13\(\frac{3}{4}\) sq ft.
Find the product.
Question 8.
1\(\frac{1}{3}\) × 1\(\frac{3}{4}\)
Answer:
1\(\frac{1}{3}\) × 1\(\frac{3}{4}\) = 2\(\frac{1}{3}\).
Explanation:
The product of 1\(\frac{1}{3}\) × 1\(\frac{3}{4}\) is
= \(\frac{4}{3}\) × \(\frac{7}{4}\)
= \(\frac{7}{3}\)
= 2\(\frac{1}{3}\).
Question 9.
2\(\frac{1}{4}\) × 3\(\frac{1}{2}\)
Answer:
2\(\frac{1}{4}\) × 3\(\frac{1}{2}\) = 7\(\frac{7}{8}\).
Explanation:
The product of 2\(\frac{1}{4}\) × 3\(\frac{1}{2}\) is
= \(\frac{9}{4}\) × \(\frac{7}{2}\)
= \(\frac{63}{8}\)
= 7\(\frac{7}{8}\).
Question 10.
Select all the equations that can be used to model the area of a piece of rectangular paper that measures 2\(\frac{1}{3}\) inches by 6\(\frac{1}{4}\) inches.
A. \(\frac{6}{3}\) × \(\frac{11}{4}\) = \(\frac{66}{12}\)
B. \(\frac{7}{3}\) × \(\frac{25}{4}\) = \(\frac{175}{12}\)
C. \(\frac{7}{3}\) × 6\(\frac{1}{4}\) = 14\(\frac{7}{12}\)
D. \(\frac{5}{3}\) × 6\(\frac{1}{4}\) = 10\(\frac{5}{12}\)
E. 2\(\frac{1}{3}\) × \(\frac{24}{4}\) = 14
F. 2\(\frac{1}{3}\) × 6\(\frac{1}{4}\) = 14\(\frac{7}{12}\)
Answer:
B, C and F.
Explanation:
The equations that are model to the area of a piece of rectangular paper that measures 2\(\frac{1}{3}\) inches by 6\(\frac{1}{4}\) inches is 2\(\frac{1}{3}\) × 6\(\frac{1}{4}\) = 14\(\frac{7}{12}\), \(\frac{7}{3}\) × 6\(\frac{1}{4}\) = 14\(\frac{7}{12}\) and \(\frac{7}{3}\) × \(\frac{25}{4}\) = \(\frac{175}{12}\).