We included HMH Into Math Grade 5 Answer Key PDF Module 9 Lesson 4 Apply Fraction Multiplication to Find Area to make students experts in learning maths.
HMH Into Math Grade 5 Module 9 Lesson 4 Answer Key Apply Fraction Multiplication to Find Area
I Can solve multiplication problems with fractions and mixed numbers to find the area of rectangles.
Step It Out
1. Toni hangs a plaque that is 5\(\frac{1}{2}\) inches wide and 8\(\frac{1}{2}\) inches long. How much wall space does the plaque cover?

Answer:
The wall space does the plaque cover is \(\frac{187}{4}\) sq in.
Explanation:
Given that Toni hangs a plaque that is 5\(\frac{1}{2}\) inches wide and 8\(\frac{1}{2}\) inches long. So the wall space does the plaque cover is 5\(\frac{1}{2}\) × 8\(\frac{1}{2}\) which is \(\frac{11}{2}\) × \(\frac{17}{2}\) = \(\frac{187}{4}\) sq in.
A. Write an equation to model the problem using fractions greater than 1.
_____________________
Answer:
\(\frac{11}{2}\) × \(\frac{17}{2}\) = \(\frac{187}{4}\) sq in.
Explanation:
The equation is \(\frac{11}{2}\) × \(\frac{17}{2}\) = \(\frac{187}{4}\) sq in.
B. Find the product from Part A. What does this product represent?
_____________________
Answer:
\(\frac{187}{4}\).
Explanation:
The product from Part A is \(\frac{187}{4}\). The product represents the area of the plaque.
C. How much wall space does the plaque cover?
_____________________
Answer:
The space cover by the plaque is \(\frac{187}{4}\) sq in.
D. What units did you use in your answer in Part C? Explain your reasoning.
_____________________
Turn and Talk Toni hangs a poster that is 8\(\frac{1}{2}\) inches wide and 11 inches long. Can the equation 17 × 11 ÷ 2 = r be used to model the amount of wall space the poster covers? How do you know?
2. Emma works to clean paintings that have been covered with dust and dirt. She must work very slowly to protect the paint. Last week, she cleaned a painting that has an area of 1\(\frac{1}{3}\) square yards. This week she cleans a painting that has an area that is \(\frac{1}{16}\) the area of the first painting. What is the area of the painting that she cleans this week?

A. Write an equation to model the problem.
___________________________
Answer:
\(\frac{4}{3}\) × \(\frac{1}{16}\) = P.
Explanation:
The equation of the problem is 1\(\frac{1}{3}\) × \(\frac{1}{16}\) which is \(\frac{4}{3}\) × \(\frac{1}{16}\) = P.
B. Solve the equation to find the area of the painting.
___________________________
Answer:
\(\frac{1}{12}\) sq.
Explanation:
The area of the painting is \(\frac{4}{3}\) × \(\frac{1}{16}\) = \(\frac{1}{12}\) sq.
C. Is your answer reasonable? How do you know?
___________________________
___________________________
___________________________
Check Understanding Math Board
Question 1.
Martina builds a pen for rabbits. The pen measures 3\(\frac{2}{3}\) ft by 4\(\frac{1}{2}\) ft. What is the area of the pen?
Answer:
The area of the pen is 16\(\frac{1}{2}\).
Explanation:
Given that the Martina builds a pen for rabbits and the pen measures 3\(\frac{2}{3}\) ft by 4\(\frac{1}{2}\) ft. So the area of the pen is 3\(\frac{2}{3}\) ft × 4\(\frac{1}{2}\) ft which is \(\frac{11}{3}\) ft × \(\frac{9}{2}\) ft = \(\frac{99}{6}\) = 16\(\frac{1}{2}\).
Write an equation to model the area of the rectangle. Find the area.
Question 2.
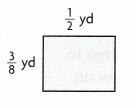
Answer:
\(\frac{3}{16}\) sq yd.
Explanation:
The area of the rectangle is \(\frac{3}{8}\) yd × \(\frac{1}{2}\) yd = \(\frac{3}{16}\) sq yd.
Question 3.
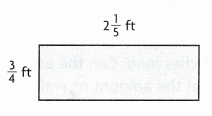
Answer:
\(\frac{33}{20}\) sq ft.
Explanation:
The area of the rectangle is \(\frac{3}{4}\) ft × 2\(\frac{1}{5}\) ft which is \(\frac{3}{4}\) ft × \(\frac{11}{5}\) = \(\frac{33}{20}\) sq ft.
On Your Own
Question 4.
The area of a bathroom is 40 square feet. The area of another room is 2\(\frac{3}{4}\) times as great as the area of the bathroom. What is the area of the other room?
Answer:
The area of the other room is 110 sq ft.
Explanation:
Given that the area of a bathroom is 40 square feet and the area of another room is 2\(\frac{3}{4}\) times as great as the area of the bathroom. So the area of the other room is 40 × 2\(\frac{3}{4}\) which is 40 × \(\frac{11}{4}\) = 110 sqft.
Find the area of the rectangle.
Question 5.
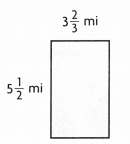
Answer:
\(\frac{121}{6}\) sq mi.
Explanation:
The area of the rectangle is 5\(\frac{1}{2}\) mi × 3\(\frac{2}{3}\) mi which is \(\frac{11}{2}\) mi × \(\frac{11}{3}\) mi = \(\frac{121}{6}\) sq mi.
Question 6.
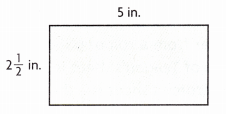
Answer:
\(\frac{25}{2}\) sq in.
Explanation:
The area of the rectangle is 2\(\frac{1}{2}\) × 5 which is \(\frac{5}{2}\) × 5 = \(\frac{25}{2}\) sq in.
Question 7.
Model with Mathematics Kyra cuts a rectangular piece of wood to make a desktop that is 5\(\frac{1}{2}\) feet long and 3\(\frac{3}{4}\) feet wide. What is the area of the desktop? Write an equation to model the area.
Answer:
The equation of the area is 5\(\frac{1}{2}\) × 3\(\frac{3}{4}\) = \(\frac{165}{8}\) sq ft.
Explanation:
Given that Kyra cuts a rectangular piece of wood to make a desktop that is 5\(\frac{1}{2}\) feet long and 3\(\frac{3}{4}\) feet wide. So the area of the desktop is 5\(\frac{1}{2}\) × 3\(\frac{3}{4}\) which is \(\frac{11}{2}\) × \(\frac{15}{4}\) = \(\frac{165}{8}\) sq ft.
Question 8.
Ms. Aman compares baking sheets in her restaurant’s kitchen. One baking sheet is 2\(\frac{1}{6}\) feet long and 1\(\frac{1}{2}\) feet wide. Another baking sheet has the same width but is 1\(\frac{1}{12}\) feet long. How much more area does the
larger baking sheet have than the smaller baking sheet?

Answer:
The difference is \(\frac{39}{24}\) sq ft.
Explanation:
Given that one baking sheet is 2\(\frac{1}{6}\) feet long and 1\(\frac{1}{2}\) feet wide. So the area is 2\(\frac{1}{6}\) × 1\(\frac{1}{2}\) which is \(\frac{13}{6}\) × \(\frac{3}{2}\) = \(\frac{13}{4}\) sq ft. Another baking sheet has the same width, but is 1\(\frac{1}{12}\) feet long. So the area is 1\(\frac{1}{12}\) × 1\(\frac{1}{2}\) which is \(\frac{13}{12}\) × \(\frac{3}{2}\) = \(\frac{39}{24}\) sq ft. So the difference will be \(\frac{13}{4}\) – \(\frac{39}{24}\) which is \(\frac{78-39}{24}\) = \(\frac{39}{24}\) sq ft.
Question 9.
A square window has side lengths that are 2\(\frac{1}{4}\) feet. What is the area of the window?
Answer:
The area of the window is \(\frac{81}{16}\) sq ft.
Explanation:
Given that the square window has side lengths that are 2\(\frac{1}{4}\) feet. So the area of the window is 2\(\frac{1}{4}\) × 2\(\frac{1}{4}\) which is \(\frac{9}{4}\) × \(\frac{9}{4}\) = \(\frac{81}{16}\) sq ft.
On Your Own
Question 10.
Model with Mathematics Catherine plants flowers in a planter that is 1\(\frac{3}{8}\) feet wide and 3\(\frac{1}{2}\) feet long. She plans to cover the entire area with fertilizer. Over how much area will she need to spread the fertilizer? Write an equation to model the area.
Answer:
The equation is \(\frac{11}{8}\) × \(\frac{7}{2}\) = \(\frac{77}{16}\) sq ft.
Explanation:
Given that Catherine plants flowers in a planter that is 1\(\frac{3}{8}\) feet wide and 3\(\frac{1}{2}\) feet long. So the equation will be 1\(\frac{3}{8}\) × 3\(\frac{1}{2}\) which is \(\frac{11}{8}\) × \(\frac{7}{2}\) = \(\frac{77}{16}\) sq ft.
Question 11.
Model with Mathematics For an art club project, Ms. Davis has students tear off sheets of paper from a roll of paper for their drawings. The area of Teagan’s sheet is 3\(\frac{3}{8}\) square feet. The area of Jerome’s sheet is \(\frac{1}{2}\) the area of Teagan’s sheet.
- Write an equation to find the area of Jerome’s sheet of paper.

- What is the area of Jerome’s sheet of paper?
Answer:
\(\frac{27}{16}\) sq ft.
Explanation:
The area is 3\(\frac{3}{8}\) × \(\frac{1}{2}\) which is \(\frac{27}{8}\) × \(\frac{1}{2}\) = \(\frac{27}{16}\) sq ft.
Question 12.
A flag has a width of \(\frac{3}{4}\) yard and a length of 1\(\frac{1}{4}\) yards. What is its area? Write an equation to model the problem.
Answer:
The equation is \(\frac{3}{4}\) × \(\frac{5}{4}\) = \(\frac{15}{16}\) sq yards.
Explanation:
Given that the flag has a width of \(\frac{3}{4}\) yard and a length of 1\(\frac{1}{4}\) yards. So the area is \(\frac{3}{4}\) × 1\(\frac{1}{4}\) which is \(\frac{3}{4}\) × \(\frac{5}{4}\) = \(\frac{15}{16}\) sq yards.
Question 13.
A rug is 2\(\frac{3}{5}\) feet wide and 4 feet long. What is its area? Write an equation to model the problem.
Answer:
The area is \(\frac{52}{5}\) sq ft.
Explanation:
Given that a rug is 2\(\frac{3}{5}\) feet wide and 4 feet long. So the area is 2\(\frac{3}{5}\) × 4 which is \(\frac{13}{5}\) × 4 = \(\frac{52}{5}\) sq ft.
Question 14.
Attend to Precision A bulletin board is 1\(\frac{1}{2}\) feet wide and 2 feet long. Gene covers \(\frac{3}{8}\) of the bulletin board with blue paper.
- What is the area of the bulletin board? __________
- How many square feet does he cover with blue paper? Write an equation to model the area.
______________________________
Answer:
The area is 3 sq feet and \(\frac{9}{8}\) sq ft.
Explanation:
Given that a bulletin board is 1\(\frac{1}{2}\) feet wide and 2 feet long. So the area is 1\(\frac{1}{2}\) × 2 which is \(\frac{3}{2}\) × 2 = 3 sq feet. And Gene covers \(\frac{3}{8}\) of the bulletin board with blue paper. So the equation is 3 × \(\frac{3}{8}\) which is \(\frac{9}{8}\) sq ft.