We included HMH Into Math Grade 5 Answer Key PDF Module 9 Lesson 1 Explore Area and Mixed Numbers to make students experts in learning maths.
HMH Into Math Grade 5 Module 9 Lesson 1 Answer Key Explore Area and Mixed Numbers
I Can use an area model to multiply mixed numbers.
Spark Your Learning
Ms. Cruz wants to use square tiles to cover the front entryway of a house. Each tile she plans to use measures \(\frac{1}{2}\) foot by \(\frac{1}{2}\) foot. What is the area of the entryway?
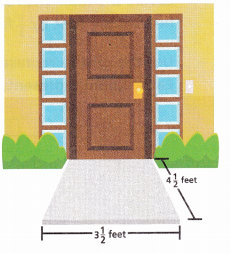
Answer:
The area will be \(\frac{1}{4}\) sq ft.
Explanation:
Given that each tile she plans to use measures \(\frac{1}{2}\) foot by \(\frac{1}{2}\) foot. So the area will be \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\) sq ft.
Draw a visual model to show how many tiles she will use. Then explain how you can use your visual model to find the area of the entryway.

Turn and Talk Describe how your method for solving the problem would change if Ms. Cruz uses smaller tiles that each measure \(\frac{1}{4}\) foot by \(\frac{1}{4}\) foot.
Build Understanding
1. Will replaces the tiles of a shower floor. The floor measures 4\(\frac{1}{3}\) feet by 3\(\frac{2}{3}\) feet. Will covers the floor with small square tiles. Each tile he uses is \(\frac{1}{3}\) foot by \(\frac{1}{3}\) foot.

Answer:
The equation will be \(\frac{13}{3}\) × \(\frac{11}{3}\) = \(\frac{143}{9}\).
Explanation:
Given that the floor measures 4\(\frac{1}{3}\) feet by 3\(\frac{2}{3}\) feet and Will covers the floor with small square tiles and Each tile he uses is \(\frac{1}{3}\) foot by \(\frac{1}{3}\) foot. So the equation is 4\(\frac{1}{3}\) × 3\(\frac{2}{3}\) which is \(\frac{13}{3}\) × \(\frac{11}{3}\) = \(\frac{143}{9}\).
Use the grid to represent the shower floor. Each square represents one tile.

A. How many tiles cover the shower floor? How can you find the number of tiles without counting them?
_______________
_______________
Answer:
The number of tiles will be 143 tiles.
Explanation:
The number of tiles without counting them is \(\frac{13}{3}\) × \(\frac{11}{3}\) = \(\frac{143}{9}\).
B. What is the area of each tile?
_______________
Answer:
\(\frac{1}{9}\) sq ft.
Explanation:
The area of each tile is \(\frac{1}{3}\) × \(\frac{1}{3}\) = \(\frac{1}{9}\) sq ft.
C. How can you use the area of each tile to find the area of the shower floor? _______________
Answer:
\(\frac{143}{9}\) sq ft.
Explanation:
The area of the shower floor is \(\frac{13}{3}\) × \(\frac{11}{3}\) = \(\frac{143}{9}\) sq ft.
D. What is the area of the shower floor? _______________
Answer:
The area of the shower floor is \(\frac{143}{9}\) sq ft.
Turn and Talk Donna models the area of the shower floor as \(\frac{13}{3}\) × \(\frac{11}{3}\). How is this like the method you used to find the area? How is it different?
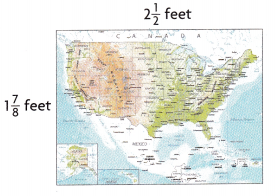
2. What is the area of this map?
You can use an area model to multiply mixed numbers.
A. How can you rewrite each mixed number as the sum of a whole number and a fraction?
_____________________
B. Use the rectangle to draw an area model by drawing a vertical line and a horizontal line to show how you broke apart the mixed numbers in Part A. Label the side lengths of the four smaller rectangles.
_____________________
C. What equations model the areas of the four smaller rectangles?
_____________________
Answer:
2\(\frac{1}{2}\) × 1\(\frac{7}{8}\)
Convert from mixed fractions into improper fractions.
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
1\(\frac{7}{8}\) = \(\frac{15}{8}\)
\(\frac{5}{2}\) × \(\frac{15}{8}\) = \(\frac{75}{16}\)
Convert from improper to mixed fraction
\(\frac{75}{16}\) = 4\(\frac{11}{16}\)
So, the area is 4\(\frac{11}{16}\) sq. feet
Check Understanding math Board
Question 1.
Pat cuts fabric for the back panel of a jacket. He measures it to be 1\(\frac{2}{3}\) feet long and 1\(\frac{1}{3}\) feet wide. He represents the area on a grid. The side length of each small square in the grid represents \(\frac{1}{3}\) foot. What is the area of the panel? Show your work.

Answer:
Given,
Pat cuts fabric for the back panel of a jacket.
He measures it to be 1\(\frac{2}{3}\) feet long and 1\(\frac{1}{3}\) feet wide.
1\(\frac{2}{3}\) × 1\(\frac{1}{3}\)
Convert from mixed fractions into improper fractions.
1\(\frac{2}{3}\) = \(\frac{5}{3}\)
1\(\frac{1}{3}\) = \(\frac{4}{3}\)
\(\frac{5}{3}\) × \(\frac{4}{3}\) = \(\frac{20}{9}\)
Convert from improper to mixed fraction
\(\frac{20}{9}\) = 2\(\frac{2}{9}\)
So, the area is 2\(\frac{2}{9}\) sq. feet
The side length of each small square in the grid represents \(\frac{1}{3}\) foot.
Area of the grid:
\(\frac{1}{3}\) × \(\frac{1}{3}\) = \(\frac{1}{9}\) sq. feet
Use the rectangle to draw an area model to solve.
Question 2.
2\(\frac{1}{3}\) × 3\(\frac{1}{2}\)

Answer:
2\(\frac{1}{3}\) × 3\(\frac{1}{2}\)
Convert from mixed fractions into improper fractions.
2\(\frac{1}{3}\) = \(\frac{7}{3}\)
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
\(\frac{7}{3}\) × \(\frac{7}{2}\) = \(\frac{49}{6}\)
Convert from improper to mixed fraction
\(\frac{49}{6}\) = 8\(\frac{1}{6}\)
So, the area is 8\(\frac{1}{6}\) sq. units
On Your Own
Question 3.
Use the grid to find 1\(\frac{1}{4}\) × 3\(\frac{1}{4}\). Let each square represent \(\frac{1}{4}\) foot by \(\frac{1}{4}\) foot.

Answer:
\(\frac{1}{4}\) foot by \(\frac{1}{4}\) = \(\frac{1}{16}\) sq. feet
1\(\frac{1}{4}\) × 3\(\frac{1}{4}\)
Convert from mixed fractions into improper fractions.
1\(\frac{1}{4}\) = \(\frac{5}{4}\)
3\(\frac{1}{4}\) = \(\frac{13}{4}\)
\(\frac{5}{4}\) × \(\frac{13}{4}\) = \(\frac{65}{16}\)
Convert from improper to mixed fraction
\(\frac{65}{16}\) = 4\(\frac{1}{16}\)
So, the area is 4\(\frac{1}{16}\) sq. feet
Question 4.
Use the rectangle to draw an area model to find 2\(\frac{1}{2}\) × 4\(\frac{2}{3}\).

Answer:
2\(\frac{1}{2}\) × 4\(\frac{2}{3}\)
Convert from mixed fractions into improper fractions.
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
4\(\frac{2}{3}\) = \(\frac{14}{3}\)
\(\frac{5}{2}\) × \(\frac{14}{3}\) = \(\frac{70}{6}\)
Convert from improper to mixed fraction
\(\frac{70}{6}\) = 11\(\frac{2}{3}\)
So, the area is 11\(\frac{2}{3}\) sq. units
Question 5.
Open Ended Chris is building a rectangular-shaped patio using square tiles. Each tile has a side length of \(\frac{1}{6}\) yard. The patio should be between 2 yards and 3 yards long and between 1 yard and 2 yards wide. Choose a length and a width for the patio. What is the area of the patio? Explain your method.
Answer:
Chris is building a rectangular-shaped patio using square tiles.
Each tile has a side length of \(\frac{1}{6}\) yard.
Area = \(\frac{1}{6}\) × \(\frac{1}{6}\) = \(\frac{1}{36}\)
The patio should be between 2 yards and 3 yards long and between 1 yard and 2 yards wide.
The length is 2\(\frac{1}{2}\)
The width is \(\frac{1}{2}\)
2\(\frac{1}{2}\) × \(\frac{1}{2}\)
\(\frac{5}{2}\) × \(\frac{1}{2}\) = \(\frac{5}{4}\) sq. yards
I’m in a Learning Mindset!
What strategies did t use to multiply mixed numbers?
_________________________
_________________________
Answer:
The strategy used to multiply mixed numbers is to convert the mixed fraction into the improper fraction and then multiply the numerator and denominator.