We included HMH Into Math Grade 5 Answer Key PDF Module 8 Lesson 3 Represent Multiplication of Whole Numbers by Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 8 Lesson 3 Answer Key Represent Multiplication of Whole Numbers by Fractions
I Can solve a problem by multiplying unit fractions using a visual model.
Spark Your Learning
A chef uses \(\frac{1}{4}\) of a package of dough. Before using this part of the package of dough, she cuts it into thirds. What fraction of a whole package is each of these smaller pieces?

Answer:
The fraction of a whole package is each of these smaller pieces is \(\frac{1}{12}\).
Explanation:
Given that a chef uses \(\frac{1}{4}\) of a package of dough. So the fraction of a whole package is each of these smaller pieces is \(\frac{1}{4}\) × \(\frac{1}{3}\) which is \(\frac{1}{12}\).
Draw a visual model to show the problem. Justify how your visual model represents the problem.

Answer:
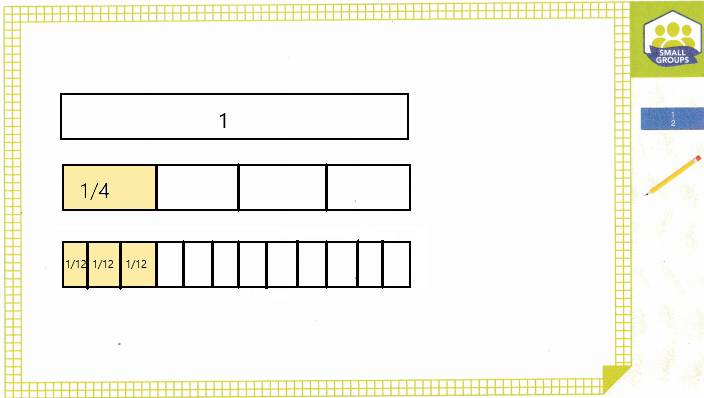
Turn and Talk How does the word “thirds” in the word problem help you set up your visual model?
Build Understanding
1. Only \(\frac{1}{3}\) of a chef’s specialty pizza is left at closing time. The chef eats \(\frac{1}{2}\) of the leftover pizza. How much of the whole pizza does the chef eat?

Answer:
The chef eat is \(\frac{1}{6}\) part.
Explanation:
Given that only \(\frac{1}{3}\) of a chef’s specialty pizza is left at closing time and the chef eats \(\frac{1}{2}\) of the leftover pizza. So the whole pizza does the chef eat is \(\frac{1}{3}\) × \(\frac{1}{2}\) which is \(\frac{1}{6}\).
Draw a visual model to show the fraction of the whole pizza that the chef eats. Justify your reasoning.

Answer:
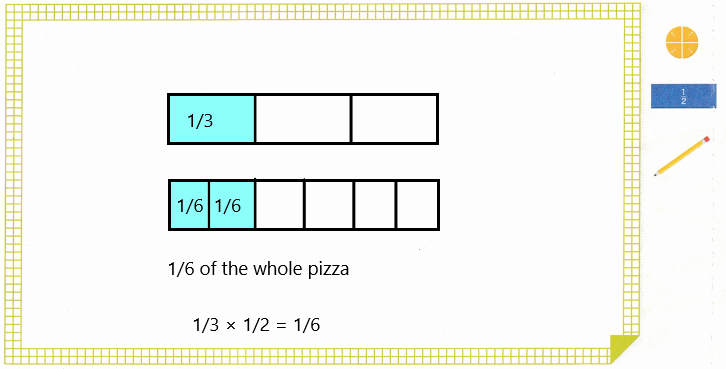
A. How do you name the fraction of the whole pizza that the chef eats? How do you know?
__________________________
__________________________
Answer:
\(\frac{1}{6}\).
Explanation:
The fraction of the whole pizza that the chef eats is \(\frac{1}{6}\).
B. What part of a whole pizza does the chef eat? Write an equation to model the problem.
__________________________
Answer:
\(\frac{1}{3}\) × \(\frac{1}{2}\) = \(\frac{1}{6}\).
Explanation:
The equation is \(\frac{1}{3}\) × \(\frac{1}{2}\) which is \(\frac{1}{6}\).
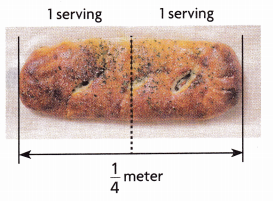
2. The chef also makes stromboli. One serving 1 serving is \(\frac{1}{2}\) of a stromboli. What fraction of a meter is the length of one serving?
Answer:
The length is \(\frac{1}{8}\) meters.
Explanation:
Given that one serving 1 serving is \(\frac{1}{2}\) of a stromboli as full serving is \(\frac{1}{4}\). So the fraction of a meter is the length of one serving is \(\frac{1}{2}\) × \(\frac{1}{4}\) which is \(\frac{1}{8}\) meters.
Use the number line to show how you can find the length of one serving.

A. What fraction of a meter is one serving of stromboli? How do you know?
________________________
________________________
________________________
Answer:
\(\frac{1}{8}\) meters.
Explanation:
The fraction of a meter in one serving of stromboli is \(\frac{1}{8}\) meters.
B. Write an equation to model the problem. ________________________
Answer:
\(\frac{1}{2}\) × \(\frac{1}{4}\) = \(\frac{1}{8}\) meters.
Explanation:
The equation will be \(\frac{1}{2}\) × \(\frac{1}{4}\) which is \(\frac{1}{8}\) meters.
Turn and Talk How would your number line change if the stromboli were cut into thirds instead of halves?
Check Understanding Math Board
Question 1.
The chef makes a rectangular pizza. At closing time, \(\frac{1}{6}\) of the pizza is left. The chef \(\frac{1}{2}\) eats of the leftover pizza. Draw a visual model to find the fraction of a whole pizza that the chef eats. Write an equation to model the problem.
Answer:
The equation is \(\frac{1}{12}\).
Explanation:
Given that the chef makes a rectangular pizza. At closing time, \(\frac{1}{6}\) of the pizza is left. The chef \(\frac{1}{2}\) eats of the leftover pizza. So the equation is \(\frac{1}{6}\) × \(\frac{1}{2}\) which is \(\frac{1}{12}\).
Question 2.
Use the number line to show \(\frac{1}{5}\) × \(\frac{1}{2}\).

Answer:
\(\frac{1}{5}\) × \(\frac{1}{2}\) = \(\frac{1}{10}\).
Explanation:
Given the equation is \(\frac{1}{5}\) × \(\frac{1}{2}\) which is \(\frac{1}{10}\).
On Your Own
Question 3.
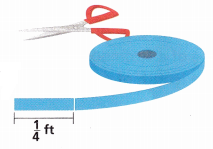
Reason A costume designer cuts the section of ribbon shown into fourths. What fraction of a foot is each piece of ribbon? ____
Answer:
The fraction is \(\frac{1}{16}\) ft.
Explanation:
Given that a costume designer cuts the section of the ribbon shown into fourths. So the fraction of a foot in each piece of ribbon is \(\frac{1}{4}\) × \(\frac{1}{4}\) which is \(\frac{1}{16}\) ft.
Question 4.
Use Tools Jackson runs \(\frac{1}{2}\) mile on Monday. On Tuesday, he runs \(\frac{1}{2}\) of the distance he ran on Monday. What fraction of a mile does Jackson run on Tuesday?
- Show your solution on the number line.

- How does the number line show the solution?
- What fraction of a mile does Jackson run on Tuesday?
Answer:
The fraction is \(\frac{1}{4}\) miles.
Explanation:
Given that Jackson runs \(\frac{1}{2}\) mile on Monday and on Tuesday, he runs \(\frac{1}{2}\) of the distance he ran on Monday. So the fraction is \(\frac{1}{2}\) × \(\frac{1}{2}\) which is \(\frac{1}{4}\) miles.
Question 5.
Draw a visual model to show \(\frac{1}{3}\) × \(\frac{1}{5}\).
Answer:
\(\frac{1}{3}\) × \(\frac{1}{5}\) = \(\frac{1}{15}\).
Explanation:
Given the equation is \(\frac{1}{3}\) × \(\frac{1}{5}\) which is \(\frac{1}{15}\).
I’m in a Learning Mindset!
How would I describe my understanding of using visual models to represent the product of two unit fractions? What can I tell myself to stay positive about my progress?