We included HMH Into Math Grade 5 Answer Key PDF Module 8 Lesson 2 Represent Multiplication of Whole Numbers by Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 8 Lesson 2 Answer Key Represent Multiplication of Whole Numbers by Fractions
I Can find the product of a whole number and a fraction using a visual model.
Spark Your Learning
Earl bakes 3 loaves of bread. He keeps \(\frac{1}{4}\) of the bread for himself and gives the rest to his neighbors. How many loaves of bread does Earl give to his neighbors?

Answer:
The number of loaves of bread does Earl give to his neighbors is 2 \(\frac{1}{4}\) loaves.
Explanation:
Given that Earl bakes 3 loaves of bread and he keeps \(\frac{1}{4}\) of the bread for himself and gives the rest to his neighbors. So the number of loaves of bread does Earl give to his neighbors is \(\frac{3}{4}\)×3 which is \(\frac{9}{4}\) = 2 \(\frac{1}{4}\) loaves.
Draw a visual model to show how you can find how many loaves he gives away. Justify your reasoning.

Turn and Talk How would your visual model change if Earl decides to keep \(\frac{1}{8}\) of the bread instead of \(\frac{1}{4}\)?
Build Understanding
1. Mrs. Fan bakes 2 cakes, each in the shape of a hexagon. She takes \(\frac{3}{4}\) of the cakes to a party.

Answer:
She takes 1\(\frac{1}{2}\) cake.
Explanation:
Given that Mrs. Fan bakes 2 cakes, each in the shape of a hexagon and she takes \(\frac{3}{4}\) of the cakes to a party. So \(\frac{3}{4}\) × 2 which is \(\frac{3}{2}\) = 1\(\frac{1}{2}\) cake she takes to the party.
Determine how much cake she takes to the party using pattern blocks and then draw a visual model to show your work.

A. How did you use pattern blocks to find the amount of cake Mrs. Fan takes to the party?
________________________________
________________________________
________________________________
B. What amount of the two cakes does Mrs. Fan take to the party?
________________________________
Answer:
1\(\frac{1}{2}\) cake.
Explanation:
The amount of cakes Mrs. Fan takes to the party is 1\(\frac{1}{2}\).
C. Write a multiplication equation to model the problem.
________________________________
Answer:
1\(\frac{1}{2}\).
Explanation:
The multiplication equation to model the problem is \(\frac{3}{4}\) × 2 which is \(\frac{3}{2}\) = 1\(\frac{1}{2}\).
Turn and Talk Why is it not appropriate to model this situation with the expression 2 × \(\frac{3}{4}\)?
2. Rashad bakes 4 equal-sized granola bars. He serves \(\frac{2}{3}\) of the bars to his friends.

Answer:
Rashad serves 2\(\frac{2}{3}\) granola bars.
Explanation:
Given that Rashad bakes 4 equal-sized granola bars and he serves \(\frac{2}{3}\) of the bars to his friends. So he serves 4 × \(\frac{2}{3}\) which is \(\frac{8}{3}\) = 1\(\frac{5}{3}\) granola bars.
Draw a visual model to show how you can find how many granola bars he serves.

A. How did you make equal-sized parts from 4 wholes? What does each part represent?
________________________________
________________________________
Answer:
To make equal-sized parts from 4 wholes we will divide them equally.
B. What does the 2 in the fraction \(\frac{2}{3}\) represent? How did you show this in your visual model?
________________________________
________________________________
Answer:
The 2 in the fraction \(\frac{2}{3}\) represent as 2 times of 3.
C. How many \(\frac{1}{3}\)-size pieces does he serve?
D. How many granola bars does he serve? Write a multiplication equation to model the problem.
Answer:
4 × \(\frac{2}{3}\).
Explanation:
The multiplication equation of the problem is 4 × \(\frac{2}{3}\) which is \(\frac{8}{3}\) = 2\(\frac{2}{3}\).
Turn and Talk How could you rearrange your visual model to find the number of whole bars Rashad serves? Explain.
3. Isa has 2 boxes of pizza. Each box has \(\frac{5}{8}\) of a pizza left. Jack says that this story context can be modeied with the equation \(\frac{5}{8}\) × 2 = 1\(\frac{1}{4}\).

A. Explain why Jack’s equation does not model the story context.
________________________________
________________________________
B. Rewrite the story context so that it can be modeled with the equation \(\frac{5}{8}\) × 2 = 1\(\frac{1}{4}\). Then draw a visual model to represent the problem.
Check Understanding Math Board
Question 1.
Al bakes 4 round cakes that are decorated like baseballs for a team party. The party guests eat \(\frac{7}{8}\) of the cakes. How many cakes do they eat in all? Draw a visual model to find the answer. Then write an equation to model the problem.
Answer:
3\(\frac{1}{2}\) cakes do they eat in all.
Explanation:
Given that Al bakes 4 round cakes that are decorated like baseballs for a team party and the party guests eat \(\frac{7}{8}\) of the cakes. So 4×\(\frac{7}{8}\) which is \(\frac{7}{2}\) = 3\(\frac{1}{2}\) cakes do they eat in all.
Question 2.
A carpenter has 10 equal-sized pieces of wood. She uses \(\frac{3}{5}\) of the wood to make a box. Use a visual model to find the number of pieces of wood that the carpenter uses. Then write an equation to model the problem.
Answer:
The number of pieces of wood that the carpenter uses is 6 pieces.
Explanation:
Given that a carpenter has 10 equal-sized pieces of wood and she uses \(\frac{3}{5}\) of the wood to make a box. So the number of pieces of wood that the carpenter uses is \(\frac{3}{5}\) × 10 which is 3×2 = 6 pieces.
On Your Own
Question 3.
Use Structure Megan makes four giant oatmeal cookies and cuts them into equal-sized pieces. She puts \(\frac{11}{12}\) of the cookies into a cookie jar. In a visual model for this situation:
- How many wholes do you need? ____
- What is the fewest number of equal-sized pieces you should cut each cookie into if you want to put \(\frac{11}{12}\) of the cookies in the jar?
__________________ - How many cookies go into the jar?
__________________
Answer:
The number of cookies will be 3\(\frac{2}{3}\).
Explanation:
Given that Megan makes four giant oatmeal cookies and cuts them into equal-sized pieces and she puts \(\frac{11}{12}\) of the cookies into a cookie jar. So the number of cookies will be \(\frac{11}{12}\) ×4 which is \(\frac{11}{3}\) = 3\(\frac{2}{3}\).
Draw a visual model to find the product.
Question 4.
\(\frac{3}{8}\) × 4 =
__________________
Answer:
\(\frac{3}{8}\) × 4 = 1\(\frac{1}{2}\).
Explanation:
Given the equation is \(\frac{3}{8}\) × 4 which is \(\frac{3}{2}\) = 1\(\frac{1}{2}\).
Question 5.
\(\frac{2}{9}\) × 3 =
__________________
Answer:
\(\frac{2}{9}\) × 3 = \(\frac{2}{3}\).
Explanation:
Given the equation is \(\frac{2}{9}\) × 3 which is \(\frac{2}{3}\).
Question 6.
Attend to Precision How could you use a visual model to show the product \(\frac{14}{15}\) × 3 ? Explain.
Answer:
\(\frac{14}{15}\) = 2\(\frac{4}{5}\).
Explanation:
The product of \(\frac{14}{15}\) × 3 which \(\frac{14}{5}\) = 2\(\frac{4}{5}\).
Question 7.
Open Ended Write a story problem for the given equation.
\(\frac{2}{3}\) × 12 =
Question 8.
Use Tools Use the number line to find \(\frac{7}{8}\) of 16.
![]()
Answer:
\(\frac{7}{8}\) × 16 = 14.
Explanation:
Given that the equation is \(\frac{7}{8}\) × 16 which is 7×2 = 14.
Use a visual model to find the product.
Question 9.
\(\frac{5}{6}\) × 3
_________________
Answer:
\(\frac{5}{6}\) × 3 = 2\(\frac{1}{2}\).
Explanation:
Given the equation is \(\frac{5}{6}\) × 3 which is \(\frac{5}{2}\) = 2\(\frac{1}{2}\).
Question 10.
\(\frac{7}{8}\) × 4
_________________
Answer:
\(\frac{7}{8}\) × 4 = 3\(\frac{1}{2}\).
Explanation:
Given the equation is \(\frac{7}{8}\) × 4 which is \(\frac{7}{2}\) = 3\(\frac{1}{2}\).
Question 11.
Write the equation that is represented by the visual model.
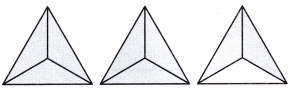
Answer:
\(\frac{8}{9}\) × 3 = 2\(\frac{2}{3}\).
Explanation:
The equation for the represented visual model is \(\frac{8}{9}\) × 3 which is \(\frac{8}{3}\) = 2\(\frac{2}{3}\).
Question 12.
Use Structure A chunk of honeycomb is made up of 8 hexagons. A beekeeper cuts out \(\frac{13}{16}\) of the honeycomb. In a visual model for this situation:
- How many wholes do you need?
_________________ - Into how many sections do you have to divide each whole?
_________________ - How many hexagons does the beekeeper cut out?
_________________
Answer:
The number of hexagons does the beekeeper cut out is 6\(\frac{1}{2}\).
Explanation:
Given that a chunk of honeycomb is made up of 8 hexagons and a beekeeper cuts out \(\frac{13}{16}\) of the honeycomb. So the number of hexagons does the beekeeper cut out is \(\frac{13}{16}\)×8 which is \(\frac{13}{2}\) = 6\(\frac{1}{2}\).
I’m in a Learning Mindset!
What type of feedback can I provide about strategies for multiplying whole numbers by fractions?
_________________
_________________