We included HMH Into Math Grade 5 Answer Key PDF Module 5 Lesson 4 Volume of Right Rectangular Prisms to make students experts in learning maths.
HMH Into Math Grade 5 Module 5 Lesson 4 Answer Key Volume of Right Rectangular Prisms
I Can find the volume of a right rectangular prism using the area of the base and the height.
Spark Your Learning
For his junior engineering club, Miguel is designing a box in the shape of a right rectangular prism that can hold exactly 12 one-inch number cubes with no extra space.

What are the dimensions and volume of a box Miguel can design? Justify your reasoning.

Answer:

Explanation:
Given for his junior engineering club, Miguel is designing a box in the shape of a right rectangular prism that can hold exactly 12 one-inch number cubes with no extra space.
The dimensions and volume of a box Miguel can design are
1. 4 X 1 X 3, volume = 12 cubic inches,
2. 4 X 3 X 1, volume = 12 cubic inches,
3. 3 X 2 X 2, volume = 12 cubic inches,
4. 3 X 4 X 1, volume = 12 cubic inches,
5. 3 X 1 X 4, volume = 12 cubic inches,
6. 2 X 1 X 6, volume = 12 cubic inches,
7. 2 X 6 X 1, volume = 12 cubic inches,
8. 1 X 1 X 12, volume = 12 cubic inches,
9. 1 X 12 X 1, volume = 12 cubic inches,
10. 1 X 6 X 2, volume = 12 cubic inches,
11. 1 X 2 X 6, volume = 12 cubic inches.
Turn and Talk Compare the possible dimensions of the different boxes Miguel can design. How are they related to the number of cubes?
Answer:
Based on number of cubes and design only dimensions can be taken,
Explanation:
Based on number of cubes and design in length wise, width wise and height wise dimensions can be taken.
Build Understanding
1. Naomi works at a health food company. She needs to stack 1-inch protein cubes into a box as shown with no extra space.

A. What is the area of the base of the box?
B. What is the volume for one layer of cubes? Explain how you know.
C. How is the volume of the prism different from the area of the base it is sitting on?
D. As each layer is added on top of the base layer, how does the volume change?
E. Complete the table to find the volume of Naomi’s box. How is the volume related to the height?
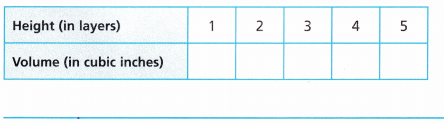
F. What is the volume of Naomi’s box? ______
Answer:
A. Area of the base is 8 sqaure inches,
B. Volume for one layer cube is 8 in,
C. Volume of prism = Area of base X height,
D. Volume increases,
E. 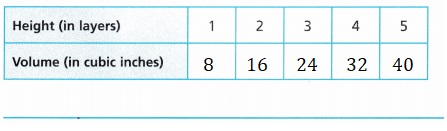
as height increased volume also got increased by
8 inches,
F. The volume of Naomi’s box is 40 cubic inches,
Explanation:
A. The area of the base of the box is as length is 4 in, width 2
4 X 2 = 8 sqaure inches,
B. The volume for one layer of cubes is
4 X 2 X 1 = 8 cubic in,
C. The surface area is the area that describes the material that will be used to cover a geometric solid.
When we determine the surface areas of a geometric solid
we take the sum of the area for each geometric form within the solid.
The volume is a measure of how much a figure can hold and is measured in cubic units.
The volume tells us something about the capacity of a figure and Volume of prism = Area of base X height.
D. As each layer is added on top of the base layer, the volume the volume gets increases for
one layer it is 4 X 2 X 1 = 8 cubic in,
for 2 layers it is 4 X 2 X 2 = 16 cubic in, so volume increases.
E. Completed the table to find the volume of Naomi’s box as
for height 1 layer volume is 4 X 2 X 1 = 8 cubic in,
for height 2 layers volume is 4 X 2 X 2 = 16 cubic in,
for height 3 layers volume is 4 X 2 X 3 = 24 cubic in,
for height 4 layers volume is 4 X 2 X 4 = 32 cubic in,
for height 5 layers volume is 4 X 2 X 5 = 40 cubic in,
As height is increased by layers the volume also gets increased by 8 inches.
F. The volume of Naomi’s box is
as length is 4 in, width is 2 in and height is 5 in,
so volume is 4 X 2 X 5 = 40 cubic inches.
Turn and Talk How can you use the terms length, width, and height to describe how to find the volume of the box? How can you use the height and the area of the base to find the volume of the box?
Answer:
Volume of the box = length X width X height,
Volume of the box = area of the base X height,
Explanation:
To describe the volume of the box by using the terms length, width, and height is
volume of the box = length X width X height and if the height and the area of the base is given then the
volume of the box = area of the base X height.
Step It Out
2. Angela is a culinary artist. She wants to pack the 1-centimeter food cubes into a container as shown.

A. What is the volume of one food cube? How do you know?
_______________________
_______________________
_______________________
B. How many 1-centimeter food cubes will she pack into the container? How can you use this amount to find the volume of the container?
_______________________
_______________________
C. What is the area of the base of the container that Angela needs?
_______________________
D. What is the height of the container?
_______________________
E. Write a numerical expression, using the height, to model the volume of the container.
_______________________
F. What is the volume of Angela’s container? How does your answer compare to your answer from Part B?
_______________________
Answer:
A. 1 cubic cm,
B. 210 cubes,
number of cubes = Volume of container ÷ Volume of one cube,
C. Area = 30 sq cm,
D. height is 7 cm,
E. V = 6 X 5 X 7,
F.Volume = 210 cubic cms,
both are equal,
A. Given Angela is a culinary artist.
She wants to pack the 1-centimeter food cubes into a container,
A. The volume of one food cube is as length is 1 cm, width is 1 cm and height is 1cm,
so volume = 1 cm X 1 cm X 1 cm = 1 cubic cm,
B. Number of 1-centimeter food cubes will she pack into the container are as number of cubes
length wise is 6 width wise 5 and height wise
there are 7 cubes so total number os food cubes are 6 X 5 X 7 = 210 cubes, As we have number of cubes =
Volume of container ÷ Volume of one cube we can find the volume of the container.
C. Area of the base with length 6 cm, width 5 cm is
Area = 6 x 5 = 30 sqaure cms.
D. The height of the given conainer is 7 cms,
E. Numerical expression using the height to model the volume of the container is
V = 6 cms X 5 cms X 7 cms,
F. The volume of Angela’s container is
V = 6 cms X 5 cms X 7 cms = 210 cubic cms,
If we compare from part B we have 210 cubes with each cube 1 cm which is equal to the volume of
container as number of cubes = Volume of container ÷ Volume of one cube so
Volume of container = number of cubes X Volume of one cube,
Volume of container = 210 cubes X 1 Cubic cm = 210 cubic cms both are similar.
Turn and Talk Suppose Angela rearranges the food cubes so that the area of the base is 42 square centimeters. What will be the new height of the container? Describe how to find the volume of this container.
Answer:
height = 5 cm,
Volume of container will be the same
210 cubic cms,
Explanation:
If Angela rearranges the food cubes so that the area of the base is 42 square centimeters the height of the container will be
Volume of container = Area of base x height,
height = Volume of container ÷ area of base,
h = 210 cubic cm ÷ 42 sq cms = 5 cm,
the volume of container will not change same as
210 cubic cm, if height is 5 cm is
42 sq cms X 5 cm = 210 cubic cms.
Step It Out
3. Angela rearranges her 1-centimeter food cubes as shown.
A. What are the length and width of the base?

B. Write a numerical expression for the area of the base. _____
C. What is the height?
_______________
D. Write a numerical expression for the volume.
_______________
E. Use your expression to find the volume. How does your answer compare with the volume you found in Step It Out 2?
_______________
A. length =7 cm,
width = 5 cm,
B. Area of base = 35 sq cms,
C. height = 6 cms,
D. V = 35 sq cm X 6 cms,
E. 210 cubic cms, both are same,
Explanation:
A. After rearranging Angela length of box is 7 cm and width of the base is 5 cm,
B. Numerical expression for the area of the base is 7 cm X 5 cm = 35 sq cms,
C. The height is 7 cms,
D. Numerical expression for the volume is
V = 35 sq cm X 6 cms,
E. The volume is V = 35 sq cm X 6 cms = 210 cubic cms, comparing with the volume I found in Step It Out 2 is same as Angela rearranged cubes so volume of the box didnot change.
Turn and Talk How can you use the properties of multiplication to find the volume of the prism mentally?
Answer:
By using Associative property of multiplication,
Explanation:
we use the associative property, as it states that the way in which factors are grouped together doesn’t affect the result of an operation,
volume of the prism = length X width X height,
By using associative property of multiplication mentally we can calculate as (length X width) X height or
length X (width X height) results will not change.
Check Understanding Math Board
Question 1.
One layer of 1-centimeter bouillon cubes is shown. If 8 layers are stacked, what is the volume of the right rectangular prism formed by the stack? Find the volume.

Answer:
Volume = 160 cubic cms,
Explanation:
As one layer of 1-centimeter bouillon cubes is shown.
If 8 layers are stacked, the volume of the right rectangular prism formed by the stack is as length is 4 cm, width 5 cm and height is 8 cm so volume is 4 cm X 5 cm X 8 cm = 160 cubic cms.
Find the volume.
Question 2.
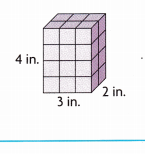
Answer:
Volume = 24 cubic in,
Explanation:
Given length as 3 in, width 2 in and height 4 in,
so volume = length X width X height,
volume = 3 in X 2 in X 4 in = 24 cubic inches.
Question 3.
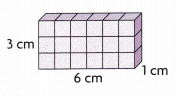
__________
Answer:
18 cubic cms,
Explanation:
Given length as 6 cm, width 1 cm and height 3 cm,
so volume = length X width X height,
volume = 6 cm X 1 cm X 3 cm = 18 cubic cm.
On Your Own
Question 4.
Reason Two layers of 1-inch cubes of cheese are placed on a platter as shown. If four more layers are added, what is the total volume of cheese? Explain how you know.

Answer:
Total volume of cheese is 144 cubic inches,
Explanation:
Given two layers of 1-inch cubes of cheese are placed on a platter as shown. If four more layers are added, the total volume of cheese will be as length is 6 inch, width is 4 inch and already we had 2 layers and 4 more layers are added so height becomes 6 inch now
volume = 6 inch X 4 inch X 6 inch = 144 cubic inches.
Find the volume.
Question 5.
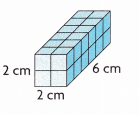
Answer:
24 cubic cms,
Explanation:
Given length as 2 cm, width 6 cm and height 2 cm,
so volume = length X width X height,
volume = 2 cm X 6 cm X 2 cm = 24 cubic cm.
Question 6.
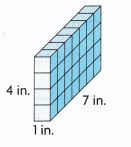
_______
Answer:
Volume = 28 cubic in,
Explanation:
Given length as 1 in, width 7 in and height 4 in,
so volume = length X width X height,
volume = 1 in X 7 in X 4 in = 28 cubic inches.
Question 7.
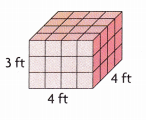
_______
Answer:
Volume = 48 cubic ft,
Explanation:
Given length as 4 ft, width 4 ft and height 3 ft,
so volume = length X width X height,
volume = 4 ft X 4 ft X 3 ft = 48 cubic ft.
Question 8.
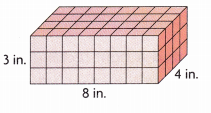
_______
Answer:
Volume = 96 cubic in,
Explanation:
Given length as 8 in, width 4 in and height 3 in,
so volume = length X width X height,
volume = 8 in X 4 in X 3 in = 96 cubic inches.
Question 9.
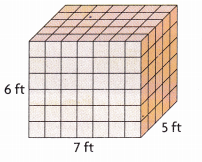
_______
Answer:
Volume = 210 cubic ft,
Explanation:
Given length as 7 ft, width 5 ft and height 6 ft,
so volume = length X width X height,
volume = 7 ft X 5 ft X 6 ft = 210 cubic ft.
Question 10.
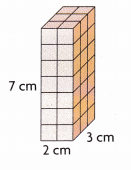
______
Answer:
42 cubic cms,
Explanation:
Given length as 2 cm, width 3 cm and height 7 cm,
so volume = length X width X height,
volume = 2 cm X 3 cm X 7 cm = 42 cubic cm.
On Your Own
Question 11.
Use Structure Danielle makes these displays using 1-inch blocks of wood. Which has the greater volume? Explain.
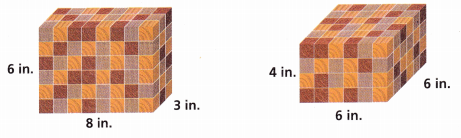
Answer:
Both displays have same volume,
Explanation:
Given Danielle makes 2 displays using 1-inch blocks of wood.
Volume of display 1 has length is 8 in, width 3 in and height is 6 in so volume is
V1 = 8 in X 3 in X 6 in = 144 cubic inches,
Volume of display 2 has length is 6 in, width 6 in and height is 4 in so volume is
V2 = 6 in X 6 in X 4 in = 144 cubic inches, both displays have same volume.
Question 12.
Consider the right rectangular prism shown.
- If the length of the edge of each cube is 1 inch, what is the volume?
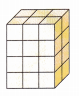
- Suppose the length of the edge of each cube is doubled to 2 inches. Write a numerical expression to model the new volume. Then find the new volume.
Answer:
1. Volume is 24 cubic inches,
2. Numerical expression = 6 in X 4 in X 8 in,
New volume = 192 cubic inches,
Explanation:
1. Given the right rectangular prism shown has length 3 inches, width 2 inches and height 4 inches,
Volume = 3 in X 2 in X 4 in = 24 cubic inches,
Now the length of the edge of each cube is doubled to 2 inches.
If a cube edges are doubled then automatically all the six sides surfaces will be doubled in all directions, causing the cube to grow in all 3 directions.
The numerical expression to model the new volume is
V = 6 in X 4 in X 8 in, the new volume is 192 cubic inches.
Question 13.
Open Ended A right rectangular prism has a square base and a volume of 144 cubic feet. What are possible dimensions of the prism?
Answer:
The possible dimensions of the prism are
1 X 1 X 144, 2 X 2 X 36, 3 x 3 X 16,
4 X 4 X 9, 6 X 6 X 4, 12 X 12 X 1,
Explanation:
Given a right rectangular prism has a square base and a volume of 144 cubic feet.
As we have volume = area of base X height, given volume as 144 cubic feet,
area of base is square means length and width are same and as 12 X 12 = 144 so all dimensions will be in between
1 and 12 only now we will take all squares and check with heights.
The possible dimensions are
1. If l and w are 1 feet, 144 = 1 X 1 X h,
h = 144 ÷ 1 = 144, so V = 1 X 1 X 144,
2. If l and w are 2 feet, 144 = 2 x 2 X h,
h = 144 ÷ 4 = 36, so V= 2 X 2 X 36,
3. If l and w are 3 feet, 144 = 3 X 3 X h,
h = 144 ÷ 9 = 16, so V = 3 X 3 X 16,
4. If l and w are 4 feet, 144 = 4 X 4 X h
h = 144 ÷ 16 = 9, so V = 4 X 4 X 9,
5. If l and w are 5 feet, 144 = 5 X 5 X h,
h = 144 ÷ 25 = 5.76 which is not possible,
6. If l and w are 6 feet 144 = 6 X 6 X h,
h = 144 ÷ 36 = 4, So V = 6 X 6 X 4,
7. If l and w are 7 feet, 144 = 7 X 7 X h,
h = 144 ÷ 49 = 2.9 which is not possible,
8. If l and w are 8 feet, 144 = 8 X 8 X h,
h = 144 ÷ 64 = 2.25 which is not possible,
9. If l and w are 9 feet, 144 = 9 X 9 X h,
h = 144 ÷ 81 = 1.77 which is not possible,
10 . If l and w are 10 feet, 144 = 10 x 10 X h,
h = 144 ÷ 100 = 1.44 which is not possible,
11. If l and w are 11 feet, 144 = 11 X 11 X h,
h = 144 ÷ 121 = 1.19 which is not possible,
12. If l and w are 12 feet, 144 = 12 X 12 X h,
h = 144 ÷ 144 = 1 feet, so V = 12 X 12 X 1.
Therefore the possible dimensions of the prism are
1 X 1 X 144, 2 X 2 X 36, 3 x 3 X 16,
4 X 4 X 9, 6 X 6 X 4, 12 X 12 X 1.
I’m in a Learning Mindset!
What do I already know that can help me find the volume on my own?
Answer:
length, width and height or area of base and height,
Explanation:
If I know length, width and height or area of base and height I can find the volume on my own.