We included HMH Into Math Grade 5 Answer Key PDF Module 4 Lesson 2 Interpret Numerical Expressions to make students experts in learning maths.
HMH Into Math Grade 5 Module 4 Lesson 2 Answer Key Interpret Numerical Expressions
I Can compare numerical expressions which are written with one expression in terms of the other.
Spark Your Learning
Michel and Sandra belong to a Remote-Control Club. They replace the batteries in their cars once a week. How does the number of batteries Michel and Sandra use in 3 weeks compare to the number of batteries they use in 1 week?

Compare the number of batteries they use. Draw to show your thinking.

Answer:
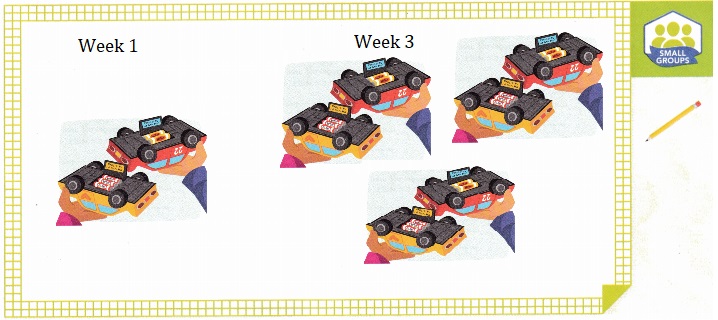
Explanation:
Compared the number of batteries Michel and Sandra use.
Drawn to show how many batteries they used in week 1 and in week 3.
A. Write numerical expressions to model the number of batteries they use in 1 week and 3 weeks.
Answer:
1 week – 2 + 3 = 5,
3 weeks – 5 X 3,
Explanation:
Michel and Sandra belong to a Remote-Control Club. They replace the batteries in their cars once a week.
Numerical expressions to model the number of batteries they use in 1 week are 2 + 3 = 5 and 3 weeks are 5 X 3.
Turn and Talk How can you check if your numerical expression is correct?
Answer:
Calculating, Drawing,
Explanation:
By drawing and calculating we can check the numerical expression is correct.
Build Understanding
1. The Remote-Control Club has two runways where airplanes take off. The sizes of the runways are shown on the map.
A. How can you model the area of Runway 1 using a numerical expression?
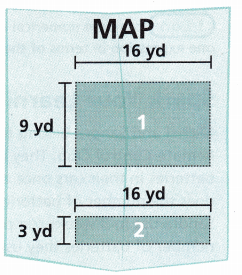
B. How can you model the area of Runway 2 using a numerical expression?
___________________________
C. Describe the length of each runway.
___________________________
D. Compare the widths of the runways. Explain how you know.
___________________________
E. Compare the areas of the runways without evaluating them.
___________________________
F. Compare the numerical expressions that model the area of each runway. Explain your reasoning.
___________________________
___________________________
Answer:
A. Area = 16 yd X 9 yd,
B. Area = 16 yd X 3 yd,
C. runway 1 – 16 yd,
runway 2 – 16 yd,
D. runway 2 < runway 1, Map,
E. Area of Runway 1> Area of runway 2,
F. 16 yd X 9 yd > 16 yd X 3 yd,
Explanation:
A. Given to find the area of Runway 1 using a numerical expression, So Runway 1 has length of 16 yd and width 9 yd so area is 16 yd X 9 yd,
B. Given to find the area of Runway 2 using a numerical expression, So Runway 2 has length of
16 yd and width 3 yd so area is 16 yd X 3 yd.
C. Given Length of runway 1 is 16 yd, runway 2 is 16 yd,
D. Runway 1 is of 9 yds and runway 2 is of 3yd so runway 2< runway 1, The sizes of the runways are shown on the map.
E. As runway 2 width is smaller than runway 1 so runway 1 will have greater area than runway 2.
F. Comparing the numerical expressions that model the area of each runway, area of runway 1 > area of runway 2,
16 yd X 9 yd > 16 yd X 3 yd, because 9 yd is more than 3 yd.
Turn and Talk Runway 1 will be expanded from 16 yards long to 32 yards long. How will the area of the expanded Runway 1 compare to the area of Runway 2?
Answer:
32 yd X 9 yd > 16 yd X 3 yd,
Explanation:
Given Runway 1 will be expanded from 16 yards long to 32 yards long. The area of the expanded Runway 1 to the area of Runway 2 will be 32 yd X 9 yd > 16 yd X 3 yd.
2. Mr. Liu follows the directions shown when he flies his remote-control airplanes.

A. How can you model the amount of oil he needs for one flight of one airplane using a numerical expression?
______________________________
B. How can you model the amount of oil he needs for one flight of four airplanes using a numerical expression?
______________________________
C. How do your numerical expressions from Parts A and B compare? Explain how you know.
______________________________
______________________________
Answer:
A. a = 5o,
B. 4a = 4 X 5o,
C. Oil needed from 1 airplane to 4 airplanes,
Explanation:
Given Mr. Liu follows the directions shown when he flies his remote-control airplanes.
A. The amount of oil he needs for one flight of one airplan using a numerical expression is
let oil is o and airpalne1 is a so a = 5o,
B. The amount of oil he needs for one flight of four airplanes using a numerical expression is
4 a = 4 X 5o,
C. For 1 airplanes to 4 airplanes, we compare oil needed.
Check Understanding Math Board
Question 1.
Each month for 2 months, Kyle buys a pack of 8 replacement tires for his remote-control car. At the end of each month, he has 1 tire left. Explain how the numerical expression for the number of tires Kyle uses in 2 months compares to the numerical expression for the number of tires he uses in 1 month.
Answer:
For 1 month – 8 – 1,
2 months 2 X (8 – 1),
2 months is twice the 1 month,
Explanation:
Given each month for 2 months, Kyle buys a pack of 8 replacement tires for his remote-control car.
At the end of each month, he has 1 tire left. the numerical expression for the number of tires he uses in 1 month is 8 -1, the numerical expression for the number of tires Kyle uses in 2 months is 2 X (8 – 1), if we compare for 2 months to 1 month the numerical expression are 2 months is twice the 1 month.
Compare the numerical expressions.
Question 2.
28 × 6 and 14 × 6
Answer:
28 X 6 > 14 X 6,
Explanation:
Given to compare the numerical expressions 28 × 6 and 14 × 6 as both sides 6 is common
and 28 is greater than 14 so 28 X 6 > 14 X 6.
Question 3.
3 × (8 + 6) and 8 + 6
Answer:
3 X (8 + 6) > (8 + 6),
Explanation:
Given to compare the numerical expressions 3 × (8 + 6) and 8 + 6 as both sides (8 + 6) is common left side it is 3 times more than (8 + 6)
so 3 X (8 + 6) > (8 + 6).
On Your Own
Question 4.
Critique Reasoning James is making banners for his dub’s airplanes to pull. Each banner is 5 feet long and is attached by a 10-foot long rope. He models the total length of the banners and rope for six airplanes with the numerical expression 6 × (5 + 10). He says the total length for six planes is five times as great as the total length needed for one plane. Correct his error.

Answer:
It’s not five times it’s six times great,
Explanation:
Given James is making banners for his dub’s airplanes to pull. Each banner is 5 feet long and is attached by a 10-foot long rope. He models the total length of the banners and rope for six airplanes with the numerical expression 6 × (5 + 10).
He says the total length for six planes is five times as great as the total length needed for one plane which error instead of five times it is six times great as the total length needed for one plane.
Compare the numerical expressions.
Question 5.
33 + 67 and 9 × (33 + 67)
Answer:
33 + 67 < 9 X (33 + 67),
Explanation:
Given to compare the numerical expressions 33 + 67 and 9 × (33 + 67) as right side it is
9 times more than left side so
33 + 67 < 9 X (33 + 67).
Question 6.
4 × (2,101 – 987) and 2,101 – 987
Answer:
4 × (2,101 – 987) > 2,101 – 987,
Explanation:
Given to compare the numerical expressions
4 × (2,101 – 987) and 2,101 – 987 as left side it is four times more than (2101 – 987) so
4 × (2,101 – 987) > 2,101 – 987.
Question 7.
Reason Explain how 56 × 9 compares to 8 × 9.
Answer:
56 > 8, 56 X 9 > 8 X 9,
Explanation:
Comparing 56 X 9 and 8 X 9 as both have multiple of 9 and 56 is greater than 8,
so 56 X 9 > 8 X 9.
I’m in a Learning Mindset!
What questions can I ask my peers to help me understand how to interpret numerical expressions?
_______________________________________________________
Answer:
1. What is numerical expression?
2. Can we use mathematical operators in numerical expressions?
3. Give some examples of numerical expressions.
4. Can we compare numerical expressions.
5. Can we use Parentheses in numerical expressions.