We included HMH Into Math Grade 5 Answer Key PDF Module 2 Lesson 3 Estimate with 2-Digit Divisors to make students experts in learning maths.
HMH Into Math Grade 5 Module 2 Lesson 3 Answer Key Estimate with 2-Digit Divisors
I Can estimate quotients of division problems using compatible numbers.
Spark Your Learning
One of Florida’s tallest buildings is 900 Biscayne Bay. It stands 650 feet tall. The building has 63 floors. If each floor is approximately the same height, about how tall is one floor of the 900 Biscayne Bay building?

Answer:
One of Florida’s tallest buildings is 900 Biscayne Bay.
It stands 650 feet tall. The building has 63 floors.
Each floor is approximately the same height.
So, 650 ÷ 63 =
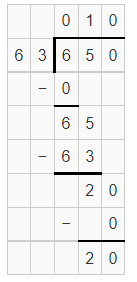
Therefore, each floor is approximately equals 10 feet.
Show your thinking.

One floor is about ____ feet tall.
Answer:
One floor is about 10 feet tall.
Turn and Talk How was the strategy you used to estimate similar to and different from estimating the product of two factors?
Build Understanding
1. The Icon Brickell South Tower in Miami is 586 feet tall and has about 60 floors. About how many feet high is each floor?
A. Write an equation to model the situation. ____
Answer:
The equation = 586 ÷ 60
B. Does the problem require you to find the exact quotient? Explain.
____________________
Answer:
No, the problem doesn’t require exact quotient. We can find the approximate quotient.
C. What is true about dividends that are compatible with a divisor of 60?
____________________
Answer:
the dividends that are compatible with a divisor of 60 should be a multiple of 3,10.
D. What two multiples of 60 are closest to 586?
____________________
Answer:
The two multiples that are closest to 586 are 540 and 600.
E. What are two estimates? Show your work.
____________________
Answer:
From the given data,
586 is near 600
so, 586 ÷ 60 = 600 ÷ 60 =10
So, each flor is about 10 feet tall.
Connect to Vocabulary
Previously, you have used mental math to compute and estimate products and quotients. Compatible numbers are numbers that are easy to compute with mentally.
F. How does each estimate compare to the actual quotient? Explain.
____________________
Answer:
586 is near 600
and 586 is near 500
So, 600 ÷ 60 = 10
500 ÷ 60 = 8.33
G. Which estimate is closer to the actual quotient? Explain.
____________________
Answer:
600 which is near to 586 is closer because it gives an approximate quotient to the actual quotient.
H. About how many feet high is each floor?
____________________
Answer:
Approximate height of floor = 10
The actual height of the floor = 9.766.
Turn and Talk Why would you want to use compatible numbers to find two estimates for the quotient?
Step It Out
2. Kadeem needs to travel to Florida for his job. The cost of the trip for 28 days is $2,475. About how much will this trip cost Kadeem each day?
A. Model the problem with an equation. Are you asked to find an estimate or an exact answer?
B. Sometimes you might have to change both the dividend and the divisor to make numbers that are compatible.
- To what number might you change 28? ____’
- Based on your answer, to what numbers might you change 2,475 to find two different estimates? ______
- How did you choose the numbers? ____
_______________________
C. Use basic facts and patterns to estimate the quotients.
D. About how much will the trip cost Kadeem each day?
_______________________
Answer:
Given,
Kadeem needs to travel to Florida for his job.
The cost of the trip for 28 days is $2,475.
$2475 is near $2500
28 is near 25
So, 2500 ÷ 25 = 100
Therefore, each day cost is $100.
Check Understanding Math Board
Question 1.
Every year, individuals race to the top of the U.S. Bank Tower in Los Angeles. The tower has 1,679 steps. A racer reaches the top in 16 minutes. About how many steps does the racer complete in one minute? ____________________
Answer:
Given,
Every year, individuals race to the top of the U.S. Bank Tower in Los Angeles.
The tower has 1,679 steps.
A racer reaches the top in 16 minutes.
so, 1679 ÷ 16
1679 is near to 1500
16 is near 15
So, 1679 ÷ 16 = 1500 ÷ 15 = 10
Therefore, the racer completes approximately 10 steps each minute.
On Your Own
Question 2.
There are 138 ounces of trail mix in a bag. You want to divide the trail mix equally among 18 smaller bags. What is a reasonable estimate for the number of ounces of trail mix that will go into each smaller bag? _____

Answer:
Given,
There are 138 ounces of trail mix in a bag.
We want to divide the trail mix equally among 18 smaller bags.
138 is near 150
18 is near 20
So, 138 ÷ 18 = 150 ÷ 20 = 7.5
Therefore, the number of ounces of trail mix that will go approximately into each smaller bag are 7.5.
Question 3.
Construct Arguments Melinda needs to travel for work. A 21-day trip costs $3,750. She says that means the trip will cost about $200 per day. Is her estimate reasonable? Explain.
Answer:
Given,
A 21-day trip costs $3,750.
3750 is near 4000
21 is near 20
So, 3750 ÷ 21 = 4000 ÷ 20 = 200
Therefore, Her estimate is reasonable.
Question 4.
Most Americans spend about 293 hours driving each year. There are 12 months in a year. What is a reasonable estimate for the number of hours most Americans drive each month? _____
Answer:
Given,
Most Americans spend about 293 hours driving each year.
There are 12 months in a year.
293 is near 300
12 is near 10
So, 293 ÷ 12 = 300 ÷ 10 = 30
Therefore, the number of hours most Americans drive each month are 30.
Use compatible numbers to find two estimates.
Question 5.
591 ÷ 70
Answer:
591 is near 630
591 ÷ 70 = 630 ÷ 70 = 9
Question 6.
2,518 ÷ 32
Answer:
2518 is near 2400
32 is near 30
2,518 ÷ 32 = 2400 ÷ 30 = 80
Question 7.
Open Ended Division of a number by a two-digit number results in a reasonable estimate of 40. Write a division equation that would result in such an estimate. ___
Answer:
811 ÷ 21
I’m in a Learning Mindset!
What types of decisions did I make when estimating quotients of 2-digit divisors?
Answer: