We included HMH Into Math Grade 5 Answer Key PDF Module 13 Lesson 2 Read and Write Decimals to Thousandths to make students experts in learning maths.
HMH Into Math Grade 5 Module 13 Lesson 2 Answer Key Read and Write Decimals to Thousandths
I Can read, write, and represent decimals to thousandths.
Spark Your Learning
A digital caliper can measure the lengths of objects to the nearest thousandth inch.

How would you read the measurement shown? Describe the place value of each digit.
Answer:
2 and five hundred eighty three thousandths
Explanation:
I will read the above measurement as 2 and five hundred eighty three thousandths
The place value of the digit 2 is ones
The place value of the digit 5 is tenths
The place value of the digit 8 is hundredths
The place value of the digit 3 is thousandths.
Turn and Talk How do you represent the decimal point when you say a decimal? Describe the numbers that are to the left and right of the decimal point.
Answer:
The decimal point is represented by the word ‘and’.
The numbers to the left of the decimal point are ones tens and hundreds from right to left
The numbers to the right of the decimal point are tenths, hundredths, thousandths and so on.
Build Understanding
Question 1.
The Great Pyramid of Giza in Egypt originally stood 146.609 meters tall.

Write the height of the pyramid in the place-value chart. Then represent the height using words.

Answer:

A. Do the two digits that are the same in 146.609 have the same place value? Explain.
Answer:
No, two digits that are same in the 146.609 do not have the same place value.
B. Since the digit in the hundredths place is 0, can you write the decimal as 146.69? Explain.
Answer:
No, we can’t write
If we write as 146.69 the number will be read as sixty nine hundredths.
C. To write 146.609 in expanded form, find the unknown numbers. Write the expanded form of 146.609.
1 × ![]() + 4 ×
+ 4 × ![]() + 6 ×
+ 6 × ![]() + 6 ×
+ 6 × ![]() + 0 ×
+ 0 × ![]() + 9 ×
+ 9 × ![]()
Answer:
1 x 100 + 4 x 10 + 6 x 1 + 6 x 0.1 + 0 x 0.01 + 9 x 0.001.
Turn and Talk How can you use the place value of the last digit in a decimal to help you read that decimal?
Answer:
The place value chart helps to read a decimal number
The number will be read as 1 hundred forty six and six hundred nine thousandths.
Question 2.
In building pyramids, Egyptians left a gap between the 0.5 mm stones as shown. Would a grain of soil that measures five thousandths millimeter fit inside the gap?

A. Represent each measure in the chart.
Answer:
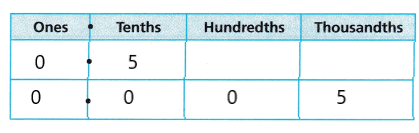
Explanation:
I represented each measure 0.5 and 0.005 in the place value chart.
B. Complete the expanded form of each measure,
gap: _________ × _________
grain of soil: _________ × _________
Answer:
Gap: 5 x 0.1
Grain of soil: 0 x 0.001
Explanation:
I wrote the expanded form of the each measure.
C. How does the value of the digit 5 in each measure compare?
Answer:
The value of the digit 5 in 0.5 is 5 tenths and the value of 5 in 0.005 is 5 thousandths.
D. Can a grain of soil fit in the gap? How do you know?
Answer:
Yes, a grain of soil can fit in the gap.
Explanation:
The grain of soil is so small so, it can fit in the gap.
Turn and Talk How can you use place value to compare the last digit of two different decimal numbers?
Answer:
We can use the place value chart to compare the last digits of the two decimals
We can understand the decimals have hundredths or thousandths.
Check Understanding
Question 1.
A digital caliper shows a measurement of 13.028 inches. Write the word form and expanded form of the number.
word form: _______________
expanded form: ____________
Answer:
Word form: Thirteen and twenty eight thousandths
Expanded form: 1 x 10 + 3 x 1 + 2 + 0 + 2 x 0.01 + 8 x 0.001
Explanation:
I wrote the word from and the expanded form of the given decimal number 13.028.
On Your Own
Question 2.
Reason What decimal has \(\frac{1}{10}\) of the value of 0.8 and 10 times as much as the value of 0.008? Explain.
Answer:
0.08
Explanation:
0.08/ 10 = 0.8
0.008 x 10 = 0.08
So, The decimal 0.08 has \(\frac{1}{10}\) of the value of 0.8 and 10 times as much as the value of 0.008.
Question 3.
Use Structure Complete the chart for the number 352.078.

Answer:
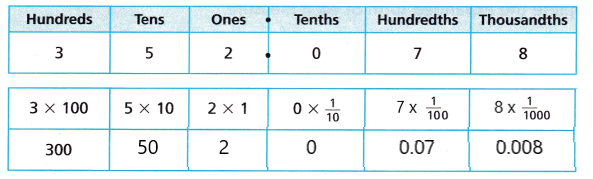
Explanation:
I completed the number chart for the number 352.078
So, the number is 3 hundred fifty two and seventy eight thousandths.
Question 4.
How would you read the decimal shown by the digital caliper?

Answer:
Zero and seven hundred ninety nine thousandths
Explanation:
The number 0.799 can be read as Zero and seven hundred ninety nine thousandths.
Write the number in standard form.
Question 5.
twenty-five thousand, forty-six and nine thousandths
Answer:
25046.009
Explanation:
The standard form for the given word form of the number is 25046.009
Question 6.
9 × 100 + 0 × 10 + 2 × 1 + 0 × 0.1 + 5 × 0.01 + 6 × 0.001
Answer:
902.056
Explanation:
The standard form for the given expanded form of the number is902.056.
I’m in a Learning Mindset!
How effective was a place-value chart in helping me read, write, and represent decimals?
Answer: