We included HMH Into Math Grade 5 Answer Key PDF Module 11 Lesson 4 Divide Unit Fractions by Whole Numbers to make students experts in learning maths.
HMH Into Math Grade 5 Module 11 Lesson 4 Answer Key Divide Unit Fractions by Whole Numbers
I Can represent division of a unit fraction by a whole number using visual fraction models and equations.
Step It Out
Question 1.
Darsha has 3 days to read \(\frac{1}{2}\) of a book. She plans to read an equal amount each day. How much of the book will Darsha read each day?

A. Model the situation with an equation. Let t represent how much of the book Darsha will read each day.
Answer:
Equation:
t = \(\frac{1}{2}\) ÷ 3,
Explanation:
Given Darsha has 3 days to read \(\frac{1}{2}\) of a book.
She plans to read an equal amount each day.
So much of the book will Darsha read each day is
let t represent how much of the book Darsha
will read each day so equation is t = \(\frac{1}{2}\) ÷ 3.
B. What part of the division equation represents the part of the book that Darsha has to read?
Answer:
Part A- \(\frac{1}{2}\),
Explanation:
Part A- \(\frac{1}{2}\) of the division equation
represents the part of the book that Darsha has to read.
C. What part of the division equation represents the number of days that Darsha has to read the book?
Answer:
Part B – 3,
Explanation:
Part B – 3 of the division equation represents the number of
days that Darsha has to read the book.
D. Represent the situation with a visual fraction model.
Answer:
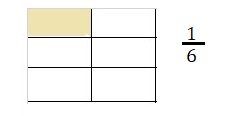
Explanation:
Represented the situation with a visual fraction model.
E. What part of the whole book does each equal part represent? How much of the book does Darsha read each day?
Answer:
t = \(\frac{1}{6}\) each equal part,
\(\frac{1}{6}\) part of the book each day,
Explanation:
t = \(\frac{1}{2}\) ÷ 3 part of the whole
book does each equal part represent,
Solving t = \(\frac{1}{2}\) X \(\frac{1}{3}\) =
\(\frac{1}{2 X 3}\) = \(\frac{1}{6}\) part of the
book does Darsha read each day.
Turn and Talk A student said that she could verify her answer by multiplying \(\frac{1}{3}\) × \(\frac{1}{2}\). Do you agree? Why or why not?
Answer:
Agree,
Explanation:
Given a student said that she could verify her answer by
multiplying \(\frac{1}{3}\) × \(\frac{1}{2}\)
I agree because commutative property of multiplication,
a X b = b X a so if it is \(\frac{1}{3}\) × \(\frac{1}{2}\) also
we get \(\frac{1}{3 X 2}\) = \(\frac{1}{6}\) value only.
Question 2.
Darsha has \(\frac{1}{3}\) of her math homework left to complete. If it takes her 4 minutes to finish it, how much of her math homework does Darsha complete each minute?
A. Write an equation that models the situation.
Answer:
Equation:
t = \(\frac{1}{3}\) ÷ 4,
Explanation:
Given Darsha has \(\frac{1}{3}\) of her math
homework left to complete. If it takes her 4 minutes
to finish it, Let t be much of her math homework does
Darsha complete each minute So the equation is
t = \(\frac{1}{3}\) ÷ 4.
B. Represent the equation on the number line.

What does the length from 0 to 1 on the number line represent?
Answer:
1 homework,
Explanation:
The length from 0 to 1 on the number line represent
1 homework.
Draw tick marks to represent the dividend on the number line from 0 to 1.
Answer:

Explanation:
Drawn tick marks to represent the dividend \(\frac{1}{3}\)
on the number line from 0 to 1.
Which section of the number line represents the dividend?
Answer:
0 to \(\frac{1}{3}\),
Explanation:
0 to \(\frac{1}{3}\) section of the number line
represents the dividend,
Shade in the section to represent the dividend.
Answer:

Explanation:
Shade in the section to represent the dividend.
Draw tick marks to represent the divisor.
Answer:

Explanation:
Drawn tick marks to represent the divisor 4.
How many equal lengths do you have?
Answer:
4 equal lengths,
Explanation:
There are 4 equal lengths.
Repeat the division of equal lengths on the entire number line. How many are there?
Answer:

Explanation:
Repeated the division of equal lengths on the entire number line.
There are 12 divisions of equal lengths.
What does the size of each equal length represent?
Answer:
Quotient,
Explanation:
The size of each equal length represents quotient.
Circle the quotient on the number line.
Answer:

Explanation:
Circled the quotient \(\frac{1}{12}\) as shown above.
C. How much of her homework does Darsha complete each minute?
Answer:
\(\frac{1}{12}\) of her work,
Explanation:
As t = \(\frac{1}{3}\) ÷ 4 =
\(\frac{1}{3}\) X \(\frac{1}{4}\) =
\(\frac{1}{3 X 4}\) = \(\frac{1}{12}\),
Therefore each minute Darsha completes \(\frac{1}{12}\)
homework.
Turn and Talk Why do you need to divide the whole number line into equal lengths and not just \(\frac{1}{3}\) of it?
Answer:
As \(\frac{1}{3}\) is on the whole number line
numerator is 1 shows whole and denominator 3 which is
bottom of fraction 3 shows number on parts on the number line,
We consider whole number line,
Check Understanding
Question 1.
Darsha writes \(\frac{1}{4}\) of a report equally over 5 days. How much of the whole report does she write each day? Write an equation to mode! the situation. Represent the equation on the number line and circle the quotient.

Answer:
Each day \(\frac{1}{20}\),
Equation:
t = \(\frac{1}{4}\) ÷ 5,
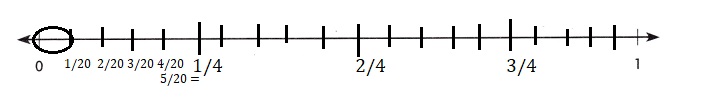
Explanation:
Given Darsha writes \(\frac{1}{4}\) of a report
equally over 5 days. Let t be the whole report does
she write each day an equation to model the situation is
t = \(\frac{1}{4}\) ÷ 5,
Represented the equation on the number line and solving
t = \(\frac{1}{4}\) X \(\frac{1}{5}\),
t = \(\frac{1}{4 x 5}\), t = \(\frac{1}{20}\),
circled the quotient t = \(\frac{1}{20}\) as shown above.
Divide. Write a related multiplication equation to solve.
Question 2.
\(\frac{1}{6}\) ÷ 9 = n
Answer:
Multiplication Equation:
n = \(\frac{1}{6}\) X \(\frac{1}{9}\),
n = \(\frac{1}{54}\),
Explanation:
Given \(\frac{1}{6}\) ÷ 9 = n to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{6}\) X \(\frac{1}{9}\),
n = \(\frac{1}{6 X 9}\),
n = \(\frac{1}{54}\).
Question 3.
n = \(\frac{1}{10}\) ÷ 6
Answer:
Multiplication Equation:
n = \(\frac{1}{10}\) X \(\frac{1}{6}\),
n = \(\frac{1}{60}\),
Explanation:
Given n = \(\frac{1}{10}\) ÷ 6 to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{10}\) X \(\frac{1}{6}\),
n = \(\frac{1}{10 X 6}\),
n = \(\frac{1}{60}\).
Question 4.
\(\frac{1}{7}\) ÷ 4 = n
Answer:
Multiplication Equation:
n = \(\frac{1}{7}\) X \(\frac{1}{4}\),
n = \(\frac{1}{28}\),
Explanation:
Given \(\frac{1}{7}\) ÷ 4 = n to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{7}\) X \(\frac{1}{4}\),
n = \(\frac{1}{7 X 4}\),
n = \(\frac{1}{28}\).
On Your Own
Question 5.
Reason is 39 a reasonable answer for \(\frac{1}{13}\) ÷ 3? Explain.
Answer:
No, not reasonable answer,
Explanation:
39 is not a reasonable answer for
\(\frac{1}{13}\) ÷ 3 as \(\frac{1}{13}\) is
unit fraction and it is divided by whole number we get
quotient less than the given unit fraction as
\(\frac{1}{13}\) X \(\frac{1}{3}\) =
\(\frac{1}{13 X 3}\) = \(\frac{1}{39}\) not
39 whole number, therefore 39 is not a reasonable
answer for \(\frac{1}{13}\) ÷ 3.
Divide. Write a related multiplication equation to solve.
Question 6.
\(\frac{1}{15}\) ÷ 5 = n
Answer:
Multiplication Equation:
n = \(\frac{1}{15}\) X \(\frac{1}{5}\),
n = \(\frac{1}{75}\),
Explanation:
Given \(\frac{1}{15}\) ÷ 5 = n to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{15}\) X \(\frac{1}{5}\),
n = \(\frac{1}{15 X 5}\),
n = \(\frac{1}{75}\).
Question 7.
n = \(\frac{1}{8}\) ÷ 12
Answer:
Multiplication Equation:
n = \(\frac{1}{8}\) X \(\frac{1}{12}\),
n = \(\frac{1}{96}\),
Explanation:
Given \(\frac{1}{8}\) ÷ 12 = n to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{8}\) X \(\frac{1}{12}\),
n = \(\frac{1}{8 X 12}\),
n = \(\frac{1}{96}\).
Question 8.
\(\frac{1}{20}\) ÷ 7 = n
Answer:
Multiplication Equation:
n = \(\frac{1}{20}\) X \(\frac{1}{7}\),
n = \(\frac{1}{140}\),
Explanation:
Given \(\frac{1}{20}\) ÷ 7 = n to write a related
multiplication equation and to solve is
we use dividing by a whole number is the same as
multiplying by its reciprocal. So multiplication equation
n = \(\frac{1}{20}\) X \(\frac{1}{7}\),
n = \(\frac{1}{20 X 7}\),
n = \(\frac{1}{140}\).
Question 9.
Open-Ended Use the number line to represent a division problem with a unit fraction divided by a whole number.

Write an equation to represent the division problem. Then circle the quotient on the number line.
Answer:
Division problem:
“Hayley is putting salsa into bowls. She has
\(\frac{1}{2}\) of a gallon of salsa and 4 bowls.
How many gallons of salsa does Hayley put into each bowl?”,

Equation:
\(\frac{1}{2}\) ÷ 4,
Quoient: \(\frac{1}{8}\),
Explanation:
Division problem:
“Hayley is putting salsa into bowls. She has
\(\frac{1}{2}\) of a gallon of salsa and 4 bowls.
How many gallons of salsa does Hayley put into each bowl?”,
Used the number line to represent a division problem
with a unit fraction divided by a whole number above
Equation to represent the division problem
\(\frac{1}{2}\) ÷ 4,
The quotient number of gallons of salsa does
Hayley put into each bowl is \(\frac{1}{2}\) X \(\frac{1}{4}\) =
\(\frac{1}{2 X 4}\) = \(\frac{1}{8}\).
Question 10.
Model with Mathematics Joshua has \(\frac{1}{3}\) pound of fertilizer for 3 flower beds. If he puts an equal amount of fertilizer in each flower bed, how much fertilizer does he put in each bed? Write an equation to model the situation. Then represent the problem using a visual model.
Answer:
\(\frac{1}{9}\) fertilizer she has put in each bed,
Equation:
\(\frac{1}{3}\) ÷ 3,

Explanation:
Given Joshua has \(\frac{1}{3}\) pound of
fertilizer for 3 flower beds. If he puts an equal amount of
fertilizer in each flower bed,
Much of fertilizer does he put in each bed is
wrote an equation to model the situation as
\(\frac{1}{3}\) ÷ 3,
Then represented the problem using a visual model above
the quotient is \(\frac{1}{3}\) ÷ 3 =
\(\frac{1}{3}\) X \(\frac{1}{3}\) =
\(\frac{1}{3 X 3}\) = \(\frac{1}{9}\),
Therefore \(\frac{1}{9}\) fertilizer she has put in each bed.
Question 11.
Open-Ended Greta solves a division problem ¡n which the quotient is \(\frac{1}{48}\). What are two possible equations that could have a quotient of \(\frac{1}{48}\)? Justify your answer.
Answer:
Equation:
1. \(\frac{1}{6}\) ÷ 4 or
\(\frac{1}{6}\) X \(\frac{1}{4}\),
2. \(\frac{1}{8}\) ÷ 3 or
\(\frac{1}{8}\) X \(\frac{1}{3}\),
Explanation:
Given Greta solves a division problem in which
the quotient is \(\frac{1}{48}\).
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48,
So the two possible equations that could have a
quotient of \(\frac{1}{48}\) are
1. \(\frac{1}{6}\) ÷ 4 or
\(\frac{1}{6}\) X \(\frac{1}{4}\),
2. \(\frac{1}{8}\) ÷ 3 or
\(\frac{1}{8}\) X \(\frac{1}{3}\).
Question 12.
Use Structure You divide \(\frac{1}{8}\) by 4. In a number line representing this division:
What would you label your large tick marks? Into how many smaller sections would you divide each equal length?
Answer:
Large ticks:
\(\frac{1}{8}\),
32 smaller sections,
Explanation:
Given I divide \(\frac{1}{8}\) by 4.
In a number line representing this division:
I would label large tick marks as \(\frac{1}{8}\),
Number of smaller sections I would divide
each equal length \(\frac{1}{8}\) ÷ 4 =
\(\frac{1}{8}\) X \(\frac{1}{4}\) =
\(\frac{1}{32}\), so 32 smaller sections.
What is the quotient?
Answer:
Quotient is \(\frac{1}{32}\),
Explanation:
Quotient is \(\frac{1}{8}\) ÷ 4 =
\(\frac{1}{8}\) X \(\frac{1}{4}\) =
\(\frac{1}{8 X 4}\) = \(\frac{1}{32}\).
Question 13.
Use Tools Kecia cuts a \(\frac{1}{4}\)-pound pepper into 6 equal-sized pieces. How much of one whole pound is each piece? Represent the problem on the number line.

Answer:
\(\frac{1}{24}\) pound each piece,

Explanation:
Given Kecia cuts a \(\frac{1}{4}\)-pound
pepper into 6 equal-sized pieces. Number of one whole pound
is each piece is \(\frac{1}{4}\) ÷ 6 =
\(\frac{1}{4}\) X \(\frac{1}{6}\) = \(\frac{1}{4 X 6}\)
\(\frac{1}{24}\). Represented the problem on the number line as shown above.