We included HMH Into Math Grade 5 Answer Key PDF Module 11 Lesson 3 Interpret and Solve Division of a Whole Number by a Unit Fraction to make students experts in learning maths.
HMH Into Math Grade 5 Module 11 Lesson 3 Answer Key Interpret and Solve Division of a Whole Number by a Unit Fraction
I Can create a story context for a given equation and use a visual fraction model to represent the quotient.
Step It Out
Question 1.
What problem can be solved by finding the number of \(\frac{1}{4}\)-size parts in 4 wholes?
A. What can be the 4 wholes?
Answer:
Dividend,
Explanation:
Given to find the number of \(\frac{1}{4}\)-size parts in 4 wholes so 4 wholes is dividend.
B. What can be the \(\frac{1}{4}\)-size parts in a whole?
Answer:
Divisor,
Explanation:
The \(\frac{1}{4}\)-size parts in a whole is divisor.
C. Write a problem that can be solved by finding the number of \(\frac{1}{4}\)-size parts in 4 wholes.
Answer:
4 ÷ \(\frac{1}{4}\),
Explaantion:
The problem that can be solved by finding the number of \(\frac{1}{4}\)-size parts in 4 wholes is
4 ÷ \(\frac{1}{4}\).
D. Use a visual fraction model to represent the problem.
Answer:
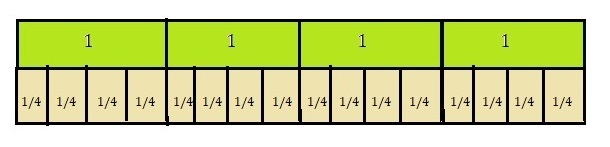
Explanation:
Represented a visual model fraction for the problem above.
E. What is the quotient, and what does it represent in the context of your problem? What equation can you write to model your problem?
Answer:
16 parts,
Equation:
4 ÷ \(\frac{1}{4}\),
Explanation:
Given what problem can be solved by finding the number of \(\frac{1}{4}\)-size parts in 4 wholes
The equation to model the problem is
4 ÷ \(\frac{1}{4}\),
The quotient is 4 X 4 = 16, 16 represents 16 parts are there in 4 wholes which are of\(\frac{1}{4}\)-size part.
Turn and Talk How would the problem change if the equation were 4 ÷ \(\frac{1}{8}\) = t?
Answer:
t = 32,
Equation:
t = 4 ÷ \(\frac{1}{8}\),
Explanation:
If the equation is changed to 4 ÷ \(\frac{1}{8}\) = t,
then t = 4 X 8 = 32.
Question 2.
Write a word problem that can be modeled by t = 5 ÷ \(\frac{1}{3}\). Then solve the problem using a visual fraction model.
A. Write a word problem that can be modeled by the division equation.
Answer:
Word problem:
“5 people shared \(\frac{1}{3}\) of cake among themselves, how many pieces of cake were there?”,
Explanation:
Asked to write a word problem that can be modeled by
t = 5 ÷ \(\frac{1}{3}\) Word problem:
“5 people shared \(\frac{1}{3}\) of cake among themselves, how many pieces of cake were there?”,
B. Use a visual model to solve.
Answer:

Explanation:
Drawn a visual model as shown above.
C. What is the quotient, and what does it represent in the context of your problem?
Answer:
Quotient : 15,
15 cake pieces,
Explanation:
Solving 5 ÷ \(\frac{1}{3}\) we get
quotient = 5 X 3 = 15,
So there were 15 pieces of cake.
Turn and Talk What are some other word problems that can be modeled by t = 5 ÷ \(\frac{1}{3}\)?
Answer:
Word problems:
1.”5 people shared \(\frac{1}{3}\) of box of apples among themselves, how many apples are there?”,
2.”5 people shared \(\frac{1}{3}\) bag of candies
among themselves how many candies are there?”,
Explanation:
Some other word problems that can be modeled by
t = 5 ÷ \(\frac{1}{3}\) are
Word problems:
1.”5 people shared \(\frac{1}{3}\) of box of apples among themselves, how many apples are there?”,
2.”5 people shared \(\frac{1}{3}\) bag of candies among themselves how many candies are there?”.
Check Understanding
Question 1.
Write and solve a division word problem for the visual fraction model.
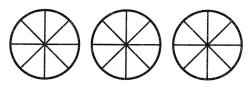
Answer:
Word problem:
” 3 pizzas are divided by \(\frac{1}{8}\) each, how many parts are there?”,
24 parts of pizza,
Explanation:
Division word problem for the visual fraction model is
” 3 pizzas are divided by \(\frac{1}{8}\) each, how many parts are there?”, solving 3 ÷ \(\frac{1}{8}\) =
3 X 8 = 24 parst of pizza.
Question 2.
Write and solve a word problem that can be modeled by r = 8 ÷ \(\frac{1}{10}\).
Answer:
Word problem:
“8 friends shared \(\frac{1}{10}\) box of candies among themselves, how many candies did they shared?”,
80 candies,
Explanation:
Word problem that can be modeled by
r = 8 ÷ \(\frac{1}{10}\) is
Word problem:
“8 friends shared \(\frac{1}{10}\) box of candies among themselves, how many candies did they shared?”,
Let r be number of candies shared among friends
so r = 8 ÷ \(\frac{1}{10}\) = 8 X 10 = 80 candies.
On Your Own
Question 3.
Use Tools Write and solve a division word problem for the visual model.
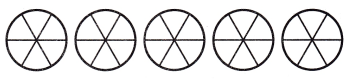
Answer:
Word problem:
“You got 5 boxes of pencils each box is divided into \(\frac{1}{6}\) part, how many total pencils are there?”,
30 pencils,
Explanation:
Wrote and solved a division word problem for the visual model as Word problem:
“You got 5 boxes of pencils each box is divided into \(\frac{1}{6}\) part, how many total pencils are there?”, 5 ÷\(\frac{1}{6}\) = 5 X 6 = 30 pencils.
Question 4.
Reason Harry has two pounds of sculpting clay. He divides the clay into \(\frac{1}{16}\)-pound blocks. Can this situation be modeled by 16 ÷ \(\frac{1}{2}\) = b and 2 ÷ \(\frac{1}{16}\) = b? Explain.
Answer:
No it can be not modeled by both 16 ÷ \(\frac{1}{2}\) = b and
2 ÷ \(\frac{1}{16}\) = b,
It can be only modeled by 2 ÷ \(\frac{1}{16}\) = b,
Explanation:
Given Harry has two pounds of sculpting clay.
He divides the clay into \(\frac{1}{16}\)-pound blocks. This situation cannot be modeled by
16 ÷ \(\frac{1}{2}\) = b and 2 ÷ \(\frac{1}{16}\) = b as the question is 2 pounds is divided by \(\frac{1}{16}\)-pound blocks not 16 pounds of sculpting clay dividived by \(\frac{1}{16}\) – pound blocks. So both cannot
be modeled only 2 ÷ \(\frac{1}{16}\) = b, can be modeled as per given situation.
Question 5.
Model with Mathematics Write and solve a word problem that can be modeled by k = 13 ÷ \(\frac{1}{10}\).
Answer:
Word problem:
“13 pizzas can be made \(\frac{1}{10}\) parts each,
how many overall parts of pizza pieces are there?”,
130 parts of pizza,
Explanation:
Asking to write and solve a word problem that can be modeled by k = 13 ÷ \(\frac{1}{10}\) is
Word problem:
“13 pizzas can be made \(\frac{1}{10}\) parts each, how many overall parts of pizza pieces are there?”,
Solving : 13 ÷ \(\frac{1}{10}\) =
13 X 10 = 130 parts of pizza.
Question 6.
Model with Mathematics Use the visual model to write and solve a division word problem.
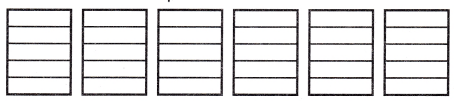
Write a division equation for the visual model.
Answer:
Division equation:
6 ÷ \(\frac{1}{5}\),
Explanation:
The division equation for the given visual model
is 6 ÷ \(\frac{1}{5}\).
Write a word problem that can be modeled by the equation.
Answer:
Word problem:
“6 whole breads are made into \(\frac{1}{5}\) slices, how many total slices of bread are there?”,
Describe what the quotient means in the context of your problem.
Answer:
30 slices of bread,
Explanation:
When 6 whole breads are made up of \(\frac{1}{5}\) slices then the quotient results number of slices are there are 6 ÷ \(\frac{1}{5}\) = 6 X 5 = 30 slices of bread.
Question 7.
Use Tools Show how you can use the triangles to make a visual model for the equation 8 ÷ \(\frac{1}{2}\) = h. Then write and solve a word problem for the visual model.
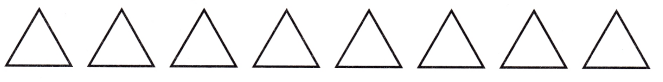
Answer:
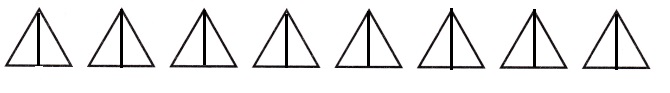
Word problem:
“There are 8 boxes of strawberries each box contains \(\frac{1}{2}\) of strawberries, how many total number of strawberries are there?”,
16 strawberries,
Explanation:
Shown how can I use the triangles to make a visual model for the equation 8 ÷ \(\frac{1}{2}\) = h, wrote and solved a word problem for the visual model as
Word problem:
“There are 8 boxes of strawberries each box contains \(\frac{1}{2}\) of strawberries, how many total number of strawberries are there?”,
let h be number of strawberries so solving
h= 8 ÷ \(\frac{1}{2}\) = 8 x 2 =16 strawberries.
Question 8.
Attend to Precision Draw a visual model to represent
s = 4 ÷ \(\frac{1}{10}\).
Write a word problem that can be represented by your visual model.
Answer:
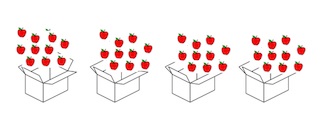
Word problem:
“There are 4 boxes of apples each box contains each box contains \(\frac{1}{10}\) of apples, total how many apples are there?”,
Explanation:
Drawn a visual model to represent
s = 4 ÷ \(\frac{1}{10}\) above,
Wrote a word problem that can be represented
by my visual model as
Word problem:
“There are 4 boxes of apples each box contains each box contains \(\frac{1}{10}\) of apples, total how many apples are there?”,
Describe what the quotient means in the context of your problem.
Answer:
40 apples,
Explanation:
Given word problem as “There are 4 boxes of apples each box contains each box contains \(\frac{1}{10}\) of apples,
total how many apples are there?”, Let s are number of apples, So number of apples are
s = 4 ÷ \(\frac{1}{10}\) = 4 X 10 = 40,
here quotient means number of apples 40.
Question 9.
Use Tools Write a word problem that can be represented by 3 ÷ \(\frac{1}{6}\) = t. Draw a visual model to help you solve the problem.
Answer:
Word problem:
“3 meters of ribbon has been cut into \(\frac{1}{6}\) part each,
How many pieces of ribbons are made”,

18 pieces of ribbon,
Explanation:
Wrote a word problem that can be represented by
3 ÷ \(\frac{1}{6}\) = t as word problem:
“3 meters of ribbon has been cut into \(\frac{1}{6}\) part each,
How many pieces of ribbons are made”,
Drawn a visual model to help and solve the problem as shown above
solving let t be number of pieces of ribbon so t = 3 ÷ \(\frac{1}{6}\) = 3 x 6 = 18 pieces of ribbon.