We included HMH Into Math Grade 5 Answer Key PDF Module 11 Lesson 2 Divide Whole Numbers by Unit Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 11 Lesson 2 Answer Key Divide Whole Numbers by Unit Fractions
I Can represent division of a whole number by a unit fraction using visual fraction models and equations.
Step It Out
Question 1.
Cat and Ann complete a new obstacle course. The course is 2 miles long, and there is an obstacle every \(\frac{1}{4}\) mile. How many obstacles are there?

A. Model the situation with an equation. Let p stand for the number of obstacles.
Answer:
Equation:
p = 2 ÷ \(\frac{1}{4}\),
Explanation:
Given Cat and Ann complete a new obstacle course.
The course is 2 miles long and there is an obstacle every \(\frac{1}{4}\) mile.
Modeling the situation with an equation.
Let p stand for the number of obstacles
Number of obstacles are there
p = 2 ÷ \(\frac{1}{4}\).
B. Represent the division equation on the number line.

How does the number line represent the dividend?
Answer:
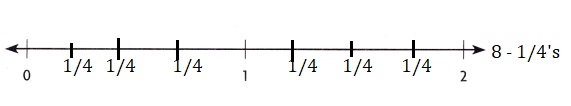
2 dividend,
Explanation:
Represented the division equation on the number line.
The number line represent the dividend 2.
Represent the divisor on the number line. Draw tick marks and label the fractions.
Answer:
Divisior on number line is \(\frac{1}{4}\),
Explanation:
Represented the divisor \(\frac{1}{4}\) on the number line. Drawn tick marks and label the fractions as shown above.
Represent the quotient. Count the number of fourths there are in 2 wholes.
Answer:
Quotient – 8
8 fourths,
Explanation:
Represented the quotient as 8,
Counted the number of 8 fourths there are in 2 wholes.
C. How many obstacles does the course have?
Answer:
8 obstacles,
Explanation:
There are 8 obstacles the course have.
Turn and Talk When representing fractions on a number line, how is the number of tick marks between each whole number related to the fraction you are representing?
Answer:
The number of tick marks represent the number parts,
Explanation:
Fractions represent parts of a whole.
So, fractions on the number line are represented by making equal parts of a whole i.e. 0 to 1 and the number of those equal parts would be the same as the number written in the denominator of the fraction.
For example, to represent 1/8 on the number line,
we have to divide 0 to 1 into 8 equal parts or 8 tick marks and mark the first part as 1/8.
Question 2.
Cat and Ann practice the rope climb at the obstacle course. The rope is 3 yards long and there is a knot every \(\frac{1}{3}\) yard. How many knots are there?

A. Model the situation with an equation. Let k represent the number of knots.
Answer:
k = 3 ÷ \(\frac{1}{3}\),
Explanation:
Given Cat and Ann practice the rope climb at the obstacle course. The rope is 3 yards long and there is a knot every \(\frac{1}{3}\) yard.
The situation with an equation and let k represent the number of knots is k = 3 ÷ \(\frac{1}{3}\).
B. Use the number line to represent the division equation.
![]()
- Represent the dividend by drawing and labeling the tick marks.
- Represent the divisor by drawing and labeling the tick marks.
- Represent the quotient by counting.
Answer:
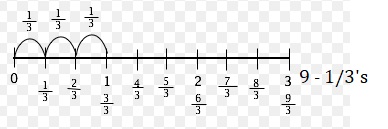
Explanation:
Used the number line to represent the division equation above,
Represented the dividend 3 by drawing and labeling the tick marks.
Represented the divisor \(\frac{1}{3}\) by drawing and labeling the tick marks.
Represented the quotient by counting 9.
C. How many knots are on the rope?
Answer:
9 knots,
Explanation:
There are 9 knots on the rope.
D. What related multiplication equation can you use to solve the problem? Explain how you know.
Answer:
Multiplication equation:
3 X 3 = 9,
Explanation:
The multiplication equation is
3 X 3 = 9, when 3 ÷ \(\frac{1}{3}\) we
write reciprocal and multiply so 3 X 3 = 9.
Turn and Talk How are the dividend, the divisor, and the quotient represented on a number line to show division?
Answer:
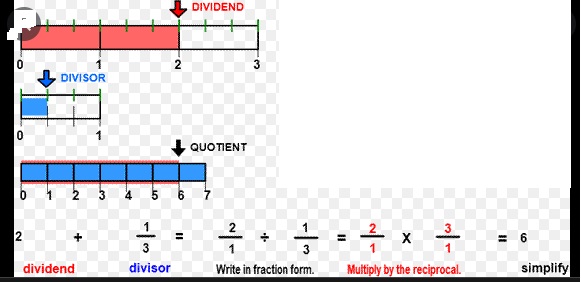
Explanation:
On the number line the division is shown as
suppose for example 2÷ \(\frac{1}{3}\) we take 2 lines from 0 to 2 on number line as dividend then divide 0 to 1 with
3 lines to represent \(\frac{1}{3}\) as divisor and conmbined 6 lines of \(\frac{1}{3}\) from 0 to 2 represents quotient as shown above.
Check Understanding
Write a division equation to model the situation. Then complete the number line and write a related multiplication equation to solve the problem.
Question 1.
A walking trail is 4 miles long. There are benches along the trail every \(\frac{1}{2}\) mile. How many benches are there?

Answer:
Division equation:
4÷ \(\frac{1}{2}\),
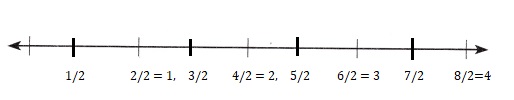
Multiplication equation:
4 X 2 = 8,
8 benches,
Explanation:
Given a walking trail is 4 miles long. There are benches along the trail every \(\frac{1}{2}\) mile.
Division equation:
4÷ \(\frac{1}{2}\),
number line is shown above,
Multiplication equation:
4 X 2 = 8,
Number of benches are there 4 ÷ \(\frac{1}{2}\) =
4 X 2 = 8 benches.
On Your Own
Question 2.
Model with Mathematics Duane and his family are playing a game. Duane scores 11 points. Each tile match is \(\frac{1}{3}\) point. Model the situation with an equation. How many tile matches does Duane make?

Answer:
Equation:
11 ÷ \(\frac{1}{3}\),
Duane makes 33 tile matches,
Explanation:
Given Duane and his family are playing a game.
Duane scores 11 points. Each tile match is \(\frac{1}{3}\) point.
The situation with an equation is 11 ÷ \(\frac{1}{3}\),
Number of tile matches does Duane make are
11 X 3 = 33 tile matches.
Question 3.
Model with Mathematics Mila swims 3 miles at the pool. She stops to take a break every \(\frac{1}{2}\) mile. How many times does Mila stop to take a break?
Model the situation with an equation.
Answer:
Equation:
3 ÷ \(\frac{1}{2}\),
6 times,
Explanation:
Given Mila swims 3 miles at the pool.
She stops to take a break every \(\frac{1}{2}\) mile. number of times does Mila stop to take a break, the situation with an equation is 3 ÷ \(\frac{1}{2}\),
3 X 2 = 6 times.
Represent the dividend, divisor, and quotient on the number line.

Answer:
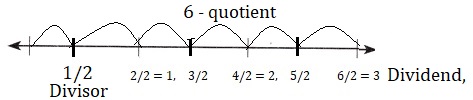
Explanation:
Represented the dividend – 3,
divisor – \(\frac{1}{2}\) and quotient 6 on the number line above.
How many times does Mila stop to take a break? Write a related multiplication equation to represent the number of times Mila stops to take a break.
Answer:
Multiplication equation:
3 X 2 = 6 times,
6 times Mila stops to take a break,
Explanation:
Multiplication equation to represent the number of times
Mila stops to take a break is 3 X 2 = 6,
So 6 times Mila stops to take a break.
Divide. Write a related multiplication equation to solve.
Question 4.
4 ÷ \(\frac{1}{5}\) = n
Answer:
n = 20,
Explanation:
Given 4 ÷ \(\frac{1}{5}\) = n,
So n = 4 X 5 = 20.
Question 5.
n = 8 ÷ \(\frac{1}{3}\)
Answer:
n = 24,
Explanation:
Given 8 ÷ \(\frac{1}{3}\) = n,
So n = 8 X 3 = 24.
Question 6.
4 ÷ \(\frac{1}{9}\) = n
Answer:
36,
Explanation:
Given 4 ÷ \(\frac{1}{9}\) = n,
So n = 4 X 9 = 36.
Question 7.
An oceanic probe descends \(\frac{1}{2}\) kilometer each minute. How many minutes will it take the probe to descend 10 kilometers into the deepest part of the ocean?
Answer:
20 minutes,
Explanation:
Given an oceanic probe descends \(\frac{1}{2}\) kilometer
each minute. Number of minutes will it take the probe to
descend 10 kilometers into the deepest part of the ocean is
10 ÷ \(\frac{1}{2}\) = 10 X 2 = 20 minutes.
Question 8.
Each bag of crackers in a box represents \(\frac{1}{15}\) of the box. How many bags of crackers are in 3 boxes?
Answer:
45 bags,
Explanation:
Given each bag of crackers in a box represents
\(\frac{1}{15}\) of the box.
Number of bags of crackers are in 3 boxes are
3 ÷ \(\frac{1}{15}\) = 3 X 15 = 45 bags.
Question 9.
Construct Arguments For what whole number value(s) of a is 17 ÷ \(\frac{1}{a}\) less than 17? Justify your reasoning.
Answer:
a = 0,
Explanation:
Asking to find what whole number value(s) of a is
17 ÷ \(\frac{1}{a}\) less than 17 is
If we take a values 2 or more than 2 it will be more
than 17,
If a = 1 then17 ÷ \(\frac{1}{a}\) =
17 X 1 = 17 which is not valid statement not less than 17,
If a = 0 then 17 X 0 < 17 statement is true, So we will take
only for values of a = 0.
Question 10.
Model with Mathematics Valerie has 6 feet of red ribbon and 25 feet of blue ribbon that she cuts into equal pieces.
How many pieces of the red ribbon does she cut if each is \(\frac{1}{12}\) foot long? Write a division equation and a related multiplication equation to solve.
Answer:
Division equation:
6 ÷ \(\frac{1}{12}\),
Multiplication equation:
6 X 12 = 72,
72 pieces of red ribbon,
Explanation:
Given Valerie has 6 feet of red ribbon that she cuts into equal pieces.
Number pieces of the red ribbon does she cut if each is
\(\frac{1}{12}\) foot long ,
division equation is 6 ÷ \(\frac{1}{12}\),
Multiplication equation: 6 X 12 = 72 upon solving we
get 72 pieces of red ribbon.
How many pieces of the blue ribbon does she cut if each is \(\frac{1}{3}\) foot long? Write a division equation and a related multiplication equation to solve.
Answer:
Division equation:
25 ÷ \(\frac{1}{3}\),
Multiplication equation:
25 X 3 = 75,
75 pieces of blue ribbon,
Explanation:
Given Valerie has 25 feet of blue ribbon that she cuts into equal pieces.
Number pieces of the blue ribbon does she cut if each is
\(\frac{1}{3}\) foot long , division equation is 25 ÷ \(\frac{1}{3}\),
Multiplication equation: 25 X 3 = 75 upon solving we
get 75 pieces of blue ribbon.
Divide. Write a related multiplication equation to solve.
Question 11.
14 ÷ \(\frac{1}{3}\) = n
Answer:
Multiplication equation:
14 X 3 = n,
n = 42,
Explanation:
Given 14 ÷ \(\frac{1}{3}\) = n, the multiplication equation is 14 X 3 = n,
so n = 42.
Question 12.
n = 5 ÷ \(\frac{1}{16}\)
Answer:
Multiplication equation:
n = 5 X 16,
n = 80,
Explanation:
Given n = 5 ÷ \(\frac{1}{16}\), the multiplication equation is n = 5 X 16,
so n = 80.
Question 13.
Open-Ended Maggie has a goal of jogging 100 miles. The distance she rules each day is the same unit fraction. What are some possible fractions of a mile she can run each day and the number of days it will take her to reach her goal? Explain how you found your answers.
Answer:
\(\frac{1}{10}\) of goal miles each day,
10 days,
Explanation:
Given Maggie has a goal of jogging 100 miles.
The distance she rules each day is the same unit fraction.
Some possible fractions of a mile she can run each day and the number of days it will take her to reach her goal,
let’s take substituting she should run
\(\frac{1}{10}\) of goal miles
she run each day, So for 10 days it is
10 ÷ \(\frac{1}{10}\) therefore
10 X 10 = 100 miles.