We included HMH Into Math Grade 5 Answer Key PDF Module 10 Lesson 5 Use Representations of Division of Whole Numbers by Unit Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 10 Lesson 5 Answer Key Use Representations of Division of Whole Numbers by Unit Fractions
I Can create a story context and use a visual fraction model to interpret the division of a whole number by a unit fraction.
Spark Your Learning
Karlus has a honey jar. Write a word problem about the honey jar that can be modeled by the expression 5 ÷ \(\frac{1}{2}\). How can a visual model be used to solve the problem?

Draw a visual model. Explain your thinking.
Answer:
Word problem:
Karlus has a honey jar of 5 lb daily he eats \(\frac{1}{2}\) part so how many days can he eat the honey?
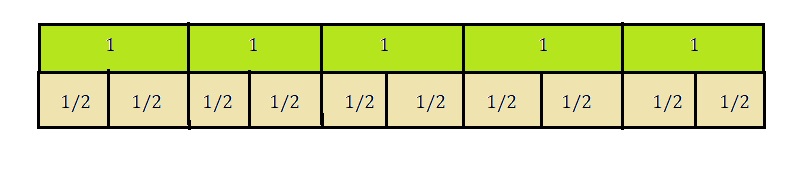
parts or portion will tell number of days, 10 days
Explanation:
Given Karlus has a honey jar. So a word problem about the honey jar that can be modeled by the expression 5 ÷ \(\frac{1}{2}\) is
Word problem:
Karlus has a honey jar of 5 lb daily he eats \(\frac{1}{2}\) part so how many days can he eat the honey?
A visual model helps us to tell how many parts or number of days the 5 lb honey can be eaten. Drawn a visual model to solve the problem
we get 5 ÷ \(\frac{1}{2}\) = 5 X 2 = 10 days.
Turn and Talk How does dividing a whole number by a unit fraction differ from dividing a unit fraction by a whole number?
Answer:
Dividing a whole number by a unit fraction the quotient will be greater than dividend,
Dividing a unit fraction by a whole number the quotient will be lesser than dividend,
Explanation:
When dividing a whole number by a fraction,
we are finding how many groups of the fraction
we can fit in the whole.
When a whole number is divided by a unit fraction,
the quotient is a whole number greater than the dividend.
When a unit fraction is divided by a whole number,
the quotient is a unit fraction less than the dividend.
Build Understanding
Question 1.
Elsa uses the plank of wood to make a craft project at the community center.
A. What word problem can you write about the plank of wood that can be modeled by 3 ÷ \(\frac{1}{4}\).
Answer:
Word problem:
Elsa used a plank which is of 3 feet long, She used\(\frac{1}{4}\) of small pieces of wood to make it. So how many small pieces of wood did Elsa used?
Explanation:
Given Elsa uses the plank of wood to make a craft project at the community center. So word problem to write about the plank of wood
that can be modeled by 3 ÷ \(\frac{1}{4}\) is
Word problem:
Elsa used a plank which is of 3 feet long, She used\(\frac{1}{4}\) of small pieces of wood to make it. So how many small pieces of wood did Elsa used?.
B. How do the quantities represent the dividend, the divisor, and the quotient?
Answer:
Dividend – 3,
Divisor – \(\frac{1}{4}\),
Quotient – 12,
Explanation:
The dividend here is plank of 3 feet long,
The divisor is \(\frac{1}{4}\) of small piece of wood and quotient is 12.
C. Draw a visual model to show the quotient.
Answer:
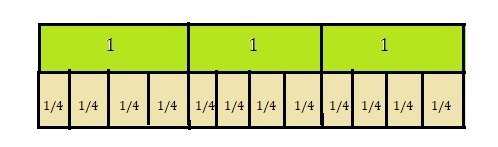
Explanation:
Drawn a visual model to show quotient as 12 above.
D. Use your visual model to write a division equation. Then write a statement to interpret the quotient for this situation.
Answer:
Division equation:
3 ÷ \(\frac{1}{4}\),
Statement:
“The quotient when 3 is divided by \(\frac{1}{4}\)“,
Explanation:
Using my visual model to write a division equation is 3 ÷ \(\frac{1}{4}\) and a statement to interpret the quotient for this situation is “The quotient when 3 is divided by \(\frac{1}{4}\)“.
Turn and Talk Elsa writes this word problem for 3 ÷ \(\frac{1}{2}\); “Mr. Grant tutors 3 students after school. He divides his time among the students equally. If the tutoring session lasts \(\frac{1}{2}\) hour, how long will he spend with each student?” Is Elsa’s problem modeled by 3 ÷ \(\frac{1}{2}\)? Explain.
Answer:
No
Explanation:
Elsa’s modeled problem is not model of 3 ÷ \(\frac{1}{2}\) as Mr.Grant tutors 3 students after school and he divided the time equally for 3 students and also given that his tutoring session lasts for \(\frac{1}{2}\), so the problem modeled should be \(\frac{1}{2}\) ÷ 3.
Question 2.
Lien prepares some appetizers for a party. Write a word problem about the appetizers that can be modeled by the expression 2 ÷ \(\frac{1}{8}\) Use a visual model to help solve the problem.
A. What word problem models the expression and includes a question about the number of equal parts?
Answer:
Word problem:
“There are 2 full plates of appetizers, each piece is of size \(\frac{1}{8}\) of the plate, then how many pieces are there in total?”.
Explanation:
Given Lien prepares some appetizers for a party. Wrote a word problem about the appetizers that can be modeled by the expression 2 ÷ \(\frac{1}{8}\),
A. Word problem that models the expression and includes a question about the number of equal parts is
Word problem:
“There are 2 full plates of appetizers, each piece is of size \(\frac{1}{8}\) of the plate, then how many pieces are there in total?”.
B. Which quantities in the story represent the dividend, the divisor, and the quotient?
Draw a visual model to show the quotient.
Answer:
Dividend – 2 full plates,
Divisor – \(\frac{1}{8}\) each piece of appetizer,
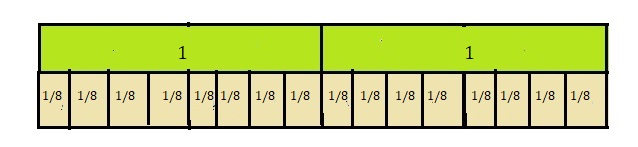
Quotient is 16 pieces of appetizer,
Explanation:
Quantities in the story that represent the dividend, the divisor, and the quotient are dividend – 2 full plates, divisor – \(\frac{1}{8}\) each piece of appetizer, Drawn a visual model to show the quotient as 16 pieces of appetizer.
C. Describe the number of equal parts in your visual model and what they represent.
Answer:
16 equal parts,
16 pieces of appetizer,
Explanation:
The number of equal parts in my visual model have 16 equal parts of \(\frac{1}{8}\), the 16 parts represents the small pieces of
appetizers in 2 plates.
D. Use your work to write a division equation. Then write a statement to interpret the quotient for this situation.
Answer:
Division equation:
2 ÷ \(\frac{1}{8}\),
Statement:
If 2 is divided among \(\frac{1}{8}\),
Explanation:
The division equation is 2 ÷ \(\frac{1}{8}\) and the statement to interpret the quotient for the situation is if 2 is divided among \(\frac{1}{8}\) how many parts are there.
Turn and Talk How would your quotient have changed if you were dividing by \(\frac{1}{4}\) instead of \(\frac{1}{8}\)? Explain.
Answer:
Quotient is 8,
Explanation:
If my quotient have changed if I were dividing by \(\frac{1}{4}\) instead of \(\frac{1}{8}\) is
2 ÷ \(\frac{1}{4}\) = 2 X 4 = 8 parts.
Step It Out
Question 3.
Zoey wants to make some raisin cookies. She has a stick of butter.

A. Write a word problem, using the stick of butter, that can be modeled by the expression 8 ÷ \(\frac{1}{3}\).
Answer:
Word problem:
Zoey uses 8 stick of butter to prepare raisin cookies if she needs to make one cookie with \(\frac{1}{3}\) of butter, So Zoey prepares how many cookies?
Explanation:
Given Zoey wants to make some raisin cookies.
She has a stick of butter. Wrote a word problem, using the stick of butter that can be modeled by the expression 8 ÷ \(\frac{1}{3}\) as
Word problem:
Zoey uses 8 stick of butter to prepare raisin cookies if she needs to make one cookie with \(\frac{1}{3}\) of butter, So Zoey prepares how many cookies?
B. Draw a visual model to show the quotient.
Answer:

quotient – 24 cookies,
Explanation:
Drawn a visual model for 8 ÷ \(\frac{1}{3}\) above,
we get quotient as 8 ÷ \(\frac{1}{3}\) = 8 X 3 = 24 cookies.
C. Interpret the quotient in the context of your word problem.
Answer:
The quotient is 24 cookies,
Explanation:
As Zoey uses 8 sticks of butter to prepare cookies as each cookie required \(\frac{1}{3}\) of butter we get quotient as number of pieces of cookies
so 8 ÷ \(\frac{1}{3}\) = 8 X 3 = 24 pieces of cookies.
Check Understanding
Question 1.
Rami buys some apples. Write a word problem that can be modeled by the expression 4 ÷ \(\frac{1}{6}\). Then draw a visual model and find the quotient.
Answer:
Word problem :
“Rami buys some apples and cuts them into \(\frac{1}{6}\) then howm many pieces of cut apples are there”,
 Quotient is 24 pieces,
Quotient is 24 pieces,
Explanation:
Given Rami buys some apples. “Rami buys some apples and cuts them into \(\frac{1}{6}\) then howm many pieces of cut apples are there”,
quotient as 4 ÷ \(\frac{1}{6}\) = 4 X 6 = 24 pieces.
Find the quotient.
Question 2.
7 ÷ \(\frac{1}{3}\) = _____________
Answer:
21,
Explanation:
The quotient for 7 ÷ \(\frac{1}{3}\) is
7 X 3 = 21.
Question 3.
9 ÷ \(\frac{1}{5}\) = ____________
Answer:
45,
Explanation:
The quotient for 9 ÷ \(\frac{1}{5}\) is
9 X 5 = 45.
On Your Own
Question 4.
Model with Mathematics Write a word problem about pizza that can be modeled by the expression 7 ÷ \(\frac{1}{8}\).
Write a word problem for the division expression.
Answer:
Word problem:
“There are 7 pizzas and each person gets \(\frac{1}{8}\) part of pizza, So how many number of friends are there?”,
Explanation:
Given to word problem about pizza that can be modeled by the expression 7 ÷ \(\frac{1}{8}\) is
Word problem:
“There are 7 pizzas and each person gets \(\frac{1}{8}\) part of pizza, So how many number of friends are there?”.
Draw a visual model to show the quotient.
Answer:

Explanation:
Drawn a visual model to show 7 ÷ \(\frac{1}{8}\) and
the quotient is 7 ÷ \(\frac{1}{8}\) = 7 X 8 = 56.
Interpret the quotient in the context of your word problem.
Answer:
56 friends eats pizzas,
Explanation:
The quotient in the context of my word problem is when there are 7 pizzas and each person gets
\(\frac{1}{8}\) part of pizza, So number of friends are there in 7 ÷ \(\frac{1}{8}\) =
7 X 8 = 56 friends.
Find the quotient.
Question 5.
10 ÷ \(\frac{1}{2}\) = _____________
Answer:
20,
Explanation:
The quotient for 10 ÷ \(\frac{1}{2}\) is
10 X 2 = 20.
Question 6.
6 ÷ \(\frac{1}{3}\) = _____________
Answer:
18,
Explanation:
The quotient for 6 ÷ \(\frac{1}{3}\) is
6 X 3 = 18.
Question 7.
3 ÷ \(\frac{1}{12}\) = _____________
Answer:
36,
Explanation:
The quotient for 3 ÷ \(\frac{1}{12}\) is
3 X 12 = 36.
Question 8.
Use Tools There are 5 sandwiches on a platter. One serving is \(\frac{1}{4}\) of a sandwich. How many servings are there? Draw a visual model to find the quotient.
Answer:
20 servings ,

Explanation:
Given there are 5 sandwiches on a platter.
One serving is \(\frac{1}{4}\) of a sandwich.
Number of servings there are 5 ÷ \(\frac{1}{4}\) =
5 X 4 = 20 servings, drawn a visual model to show the quotient as 20 servings above.
Question 9.
Attend to Precision Ian writes a word problem that can be modeled by the expression 2 ÷ \(\frac{1}{3}\).
Mycaela has 2 jars of peanut butter. She needs \(\frac{1}{3}\) cup for one batch of oatmeal bites. How many batches of oatmeal bites can she make?
Does the word problem match the division expression? Explain.
Answer:
Yes it matches,
Explanation:
Given Ian writes a word problem that can be modeled by the expression 2 ÷ \(\frac{1}{3}\).
Mycaela has 2 jars of peanut butter. She needs \(\frac{1}{3}\) cup for one batch of oatmeal bites.
So many batches of oatmeal bites can she make are
2 ÷ \(\frac{1}{3}\) = 2 X 3 = 6 matches ,
so the word problem matches the division expression
as 2 ÷ \(\frac{1}{3}\) = 2 X 3 = 6 and
Mycaela makes 6 batches both are the same matches.
Question 10.
Use Repeated Reasoning Rami divides a whole number by a unit fraction, and then divides the quotient by another unit fraction, is the second quotient less than or greater than the original whole number? Explain.
Answer:
Greater than the original whole number,
Explanation:
Given Rami divides a whole number by a unit fraction and then divides the quotient by another unit fraction is the second quotient less than or greater than the original whole number. As we know when dividing a whole number by a fraction we are finding how many groups of the fraction we can fit in the whole.
When a whole number is divided by a unit fraction, the quotient is a whole number greater than the dividend.
So the second quotient will be still greater than the original number.
Question 11.
Open-Ended Mae uses the expression 5 ÷ \(\frac{1}{6}\) to solve a problem.
Write a word problem that can be modeled by the expression.
Answer:
Word problem:
“Mae has 5 pages stamp book in that she uses to stick stamps each stamp uses \(\frac{1}{6}\) of the page, how many stamps can be sticked in the book?”,
Explanation:
Given Mae uses the expression 5 ÷ \(\frac{1}{6}\) to solve a problem.
The word problem that can be modeled by the expression is
Word problem:
“Mae has 5 pages stamp book in that she uses to stick stamps each stamp uses \(\frac{1}{6}\) of the page, how many stamps can be sticked in the book?”,.
Draw a visual representation to show the quotient.
Answer:

Explanation:
Drawn a visual representation to show the quotient as
5 ÷ \(\frac{1}{6}\) = 5 X 6 = 30 stamps.
Write an equation to model the problem. Interpret the quotient for the situation.
Answer:
Equation:
Number of stamps n = 5 ÷ \(\frac{1}{6}\),
Explanation:
The equation to model the problem is let n be the number of stamps can be stuck are when 5 pages are divided by \(\frac{1}{6}\) the equation is number of stamps n = 5 ÷ \(\frac{1}{6}\) so the quotient is 5 X 6 = 30 stamps.
I’m in a Learning Mindset!
How does explaining my strategy help me write division word problems and model the quotient?
Answer:
Make equal groups, use an area model, using the relationship between multiplication and division or using partial quotients,
Explanation:
To solve division problems we use strategies how we can make equal groups or create equal groups with place values and use multiplication and easily model the quotient. Explaining each part of a division equation as the dividend, the divisor, and the quotient helps me to write division word problems and model the quotient easily.