We included HMH Into Math Grade 5 Answer Key PDF Module 10 Lesson 4 Represent and Find the Number of Equal-Sized Parts to make students experts in learning maths.
HMH Into Math Grade 5 Module 10 Lesson 4 Answer Key Represent and Find the Number of Equal-Sized Parts
I Can divide a whole number by a unit fraction using a visual fraction model.
Spark Your Learning
A nature preserve is 5 miles wide. A ranger divides the entire preserve into |-mile wide sections for different tours. How many sections does the nature preserve have for different tours?

Justify your answer.
Answer:
5 sections does the nature preserve,
Explanation:
Given a nature preserve is 5 miles wide. A ranger divides
the entire preserve into |-mile wide sections for
different tours. Number of sections does the nature
preserve have for different tours is 5 miles ÷ 1 mile =
5 sections.
Turn and Talk What if the ranger chose to divide the preserve into sections that were \(\frac{1}{6}\)-mile wide? How would your answer change?
Answer:
30 sections does the nature preserve,
Explanation:
If the ranger chose to divide the preserve into sections
that were \(\frac{1}{6}\)-mile wide then it is clear
that nature preserve is 5 miles wide. so ranger divides the
entire preserve into 5 ÷ \(\frac{1}{6}\) sections =
5 X 6 = 30 sections for different tours.
Build Understanding
Question 1.
The nature preserve has a 3-mile long trail for birdwatchers. The ranger divides the trail into \(\frac{1}{2}\)-mile sections and names each section after a different bird. How many of these sections does the trail have?

A. Complete to describe the situation and model it with an expression.
The trail is __________ miles long and is divided into _________ mile sections. This can be modeled by the expression ___________.
Answer:
The trail is 3 miles long and is divided into
\(\frac{1}{2}\) mile sections.
This can be modeled by the expression
3 ÷ \(\frac{1}{2}\),
6 sections,
Explanation:
Given to complete and describe the situation and
model it with an expression so it is
The trail is 3 miles long and is divided into
\(\frac{1}{2}\) mile sections.
This can be modeled by the expression
3 ÷ \(\frac{1}{2}\), number of sections is
3 X 2 = 6 sections.
B. Represent the situation with the number line.

How is the dividend represented on the number line?
Answer:
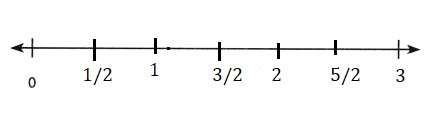
Dividend is represented by 3 on the number line,
Explanation:
Represented the situation with the number line as shown above,
and Dividend is represented by 3 on the number line.
How is the divisor represented on the number line?
Answer:
Divisor – \(\frac{1}{2}\),
Explanation:
The divisor is represented by \(\frac{1}{2}\) on the
number line.
How is the quotient represented on the number line?
Answer:
6 parts,
Explanation:
The quotient is represented by 6 parts on the number line.
C. What division equation can you write? Interpret your answer in this situation.
Answer:
Division equation:
3 ÷ \(\frac{1}{2}\),
Explanation:
When 3 miles is divided by \(\frac{1}{2}\) we
will get 6 parts of \(\frac{1}{2}\) mile.
Turn and Talk How can you find out how many \(\frac{1}{2}\)-mile sections are ¡n 9 miles?
Answer:
Dividing 9 by \(\frac{1}{2}\),
Explanation:
To find out how many \(\frac{1}{2}\)-mile
sections are ¡n 9 miles we divide 9 miles by
\(\frac{1}{2}\)– mile as 9 miles ÷ \(\frac{1}{2}\)-mile
we get number of sections.
Step It Out
Question 2.
Jon’s lawn mower uses \(\frac{1}{4}\) gallon of gas each time he mows the lawn. Jon has 3 gallons of gas in a container. How many times can he mow the lawn before he needs to refill the container?
A. Represent the amount of gas in the container. Draw rectangles to show each gallon.
Answer:
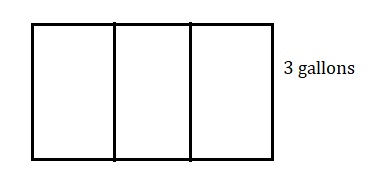
Explanation:
Drawn 3 boxes to show each gallons that Jon has
3 gallons of gas in a container.
B. Divide each rectangle from Part A into fourths to represent the amount of gas needed to mow the lawn.
Answer:
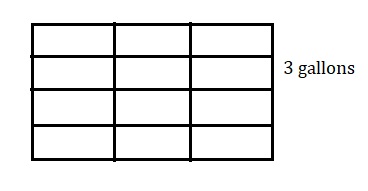
Explanation:
Divided each rectangle from Part A into fourths to
represent the amount of gas needed to mow the lawn.
C. Count the number of equal parts in the smaller rectangles to find the quotient. Write a division equation to model the problem and explain what the quotient means in this situation.
Answer:
12 equal parts,
Division equation:
3 ÷ \(\frac{1}{4}\),
Explanation:
Counted the number of equal parts in the smaller
rectangles to find the quotient.
There are 12 equal parts, a division equation to
model the problem is 3 ÷ \(\frac{1}{4}\),
the quotient means in this situation is when 3 is divided
into fourths parts we get 12 equal parts as
3 ÷ \(\frac{1}{4}\) = 3 X 4 = 12 parts.
Check Understanding
Draw a visual model to solve the problem, and then write a division equation.
Question 1.
Tim serves \(\frac{1}{5}\) pound of cat food each day from a 2-pound bag. How many days will this bag last?
Answer:
10 days it will last,
Explanation:
Given Tim serves \(\frac{1}{5}\) pound of cat
food each day from a 2-pound bag. Number days will
this bag last is 2 ÷ \(\frac{1}{5}\) = 2 X 5 = 10 days.
On Your Own
Question 2.
Model with Mathematics Write a division equation that represents the visual model.
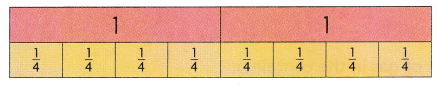
Answer:
2 ÷ \(\frac{1}{4}\),
Explanation:
As we see the visual model 2 is divided into
\(\frac{1}{4}\), so the division equation
that representsthe visual model is 2 ÷ \(\frac{1}{4}\).
Question 3.
Draw a visual model to represent 2 ÷ \(\frac{1}{6}\). Then find the quotient.
2 ÷ \(\frac{1}{6}\) = ___________
Answer:

Explanation:
Drawn a visual model to represent 2 ÷ \(\frac{1}{6}\)
above, the quotient of 2 ÷ \(\frac{1}{6}\) is
2 X 6 = 12.
Question 4.
Tyra has 4 liters of distilled water for a chemistry experiment. This is \(\frac{1}{5}\) of the amount she needs. How much distilled water does she need?
Answer:
20 liters,
Explanation:
Given Tyra has 4 liters of distilled water for a
chemistry experiment. This is \(\frac{1}{5}\) of
the amount she needs. So distilled water does she need is
4 ÷ \(\frac{1}{5}\) = 4 X 5 = 20 liters.
Question 5.
Model with Mathematics Draw visual models to complete the equations.
2 ÷ \(\frac{1}{2}\) = ___________
Answer:
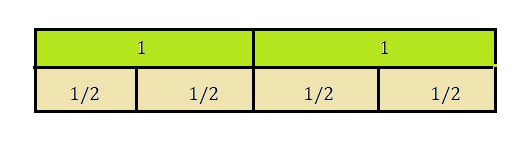
4,
Explanation:
Drawn visual models to complete the equation
2 ÷ \(\frac{1}{2}\) as shown above,
2 X 2 = 4.
2 ÷ \(\frac{1}{3}\) = ___________
Answer:
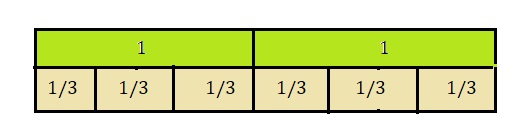
6,
Explanation:
Drawn visual models to complete the equation
2 ÷ \(\frac{1}{3}\) as shown above,
2 X 3 = 6.
How are the two equations the same? Explain your thinking.
Answer:
Whole is 2,
Explanation:
Both have same whole portion or part as 2.
I’m in a Learning Mindset!
How is using visual models effective in solving a problem?
Answer:
Easier to remember information presented in
picture form using visual models,
Explanation:
Visual models provide a useful tool for ‘concretising’ complex and abstract ideas. The human brain responds positively to information packaged in creative and visual ways, which is why throughout our daily lives we are constantly bombarded with visual imagery and stimuli. It is often easier to remember information presented in picture form than as a string of words, and visual models provide succinct and organised summaries of information.
Visual models can also demonstrate relationships between different items and, when shown dynamically can show how those relationships change and evolve.
So therefore it is easier to remember information presented in picture form using visual models to solve a problem.