We included HMH Into Math Grade 5 Answer Key PDF Module 10 Lesson 3 Use Representations of Division of Unit Fractions by Whole Numbers to make students experts in learning maths.
HMH Into Math Grade 5 Module 10 Lesson 3 Answer Key Use Representations of Division of Unit Fractions by Whole Numbers
I Can create a story context and use a visual fraction model to interpret the division of a unit fraction by a whole number.
Spark Your Learning
Darren thinks about how he can use division of unit fractions by whole numbers in his cooking class. He considers the expression \(\frac{1}{2}\) ÷ 8. What word problem can be written for \(\frac{1}{2}\) ÷ 8? Draw a visual model to show the quotient, and then explain what it represents.

Answer:
Darren prepares soup from \(\frac{1}{2}\) of flour and
divides among 8 people, each people will get how much portion
of flour soup?
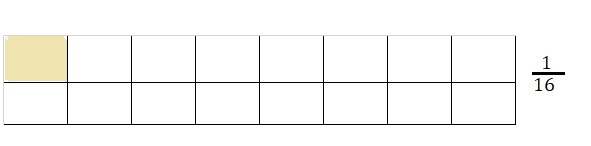
Explanation:
Given Darren thinks about how he can use division of
unit fractions by whole numbers in his cooking class.
He considers the expression \(\frac{1}{2}\) ÷ 8.
word problem can be written for \(\frac{1}{2}\) ÷ 8 is
Darren prepares soup from \(\frac{1}{2}\) of flour and
divides among 8 people, each people will get how much portion
of flour soup?
Drawn a visual model above to show the quotient as
\(\frac{1}{2}\) ÷ 8 =\(\frac{1}{2}\) X \(\frac{1}{8}\) =
\(\frac{1}{2 X 8}\) = \(\frac{1}{16}\).
Turn and Talk When dividing a fraction by a whole number, what do you notice about the values of the dividend and the quotient? Explain how they compare.
Answer:
The divided and quotient value will be less,
Explanation:
Dividing fractions with whole numbers results in a value
less than the given fraction. It is because we are dividing
it into smaller equal parts and the quotient obtained will
be the value of one part out of those.
Build Understanding
Question 1.
Darren considers situations in which a fractional quantity is divided into equal groups. Darren thinks about the expression \(\frac{1}{4}\) ÷ 2.

A. Describe a situation in which \(\frac{1}{4}\) of an item can be divided into 2 equal parts. How do the quantities represent the dividend, the divisor, and the quotient?
Answer:
Situation:
Darren prepares tea using \(\frac{1}{4}\) jug of 1000 ml milk and
distributes among two persons each person will get
how much quantity of milk?
Dividend – 2 persons,
Divisor – \(\frac{1}{4}\) jug of milk,
Quotient – \(\frac{1}{8}\) of 1,000 ml milk,
Explanation:
Given Darren considers situations in which a fractional quantity is divided into equal groups. Darren thinks about the expression \(\frac{1}{4}\) ÷ 2.
Situation:
Darren prepares tea using \(\frac{1}{4}\) jug of 1000 ml milk and
distributes among two persons each person will get
how much quantity of milk? Here Dividend is 2 persons,
Divisor is \(\frac{1}{4}\) ju of milk and
Quotient is \(\frac{1}{8}\) of 1,000 ml milk.
B. What word problem can you write that can be modeled by \(\frac{1}{4}\) ÷ 2, and includes a question about the size of each part?
Draw a visual model to show the quotient.
Answer:
Word problem:
Darren gives \(\frac{1}{4}\) of his pencils among
his two freinds, each freind will get how much part,
\(\frac{1}{4}\) is dividend,
2 is divisor and \(\frac{1}{8}\) is
quotient,
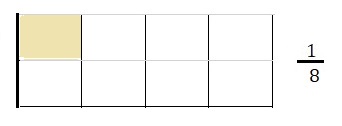
Explanation:
Darren gives \(\frac{1}{4}\) of his pencils among
his two freinds, each freind will get how much part,
\(\frac{1}{4}\) of pencils is dividend, 2 friends are
divisor and each will get \(\frac{1}{8}\) is quotient.
Drawn a visual model to show the quotient above.
C. Use your visual model to write a division equation. Then explain what the quotient represents.
Answer:
Division equation : \(\frac{1}{4}\) ÷ 2,
quotient \(\frac{1}{2}\) represents what
quanity we will get,
Explanation:
Used the visual model and wrote a
division equations as \(\frac{1}{4}\) ÷ 2,
we have rule to divide a fraction by a whole number,
multiply the given fraction by the reciprocal of whole numbers.
So \(\frac{1}{4}\) ÷ 2 is \(\frac{1}{4}\) X \(\frac{1}{2}\) =
\(\frac{1}{4 X 2}\) = \(\frac{1}{8}\).
The quotient represents \(\frac{1}{4}\) is been divided
by 2 we get each part as \(\frac{1}{8}\).
Turn and Talk Discuss different situations that can be represented by \(\frac{1}{4}\) ÷ 2. What types of quantities can be modeled by the dividend?
Answer:
Situation 1:
Darren has \(\frac{1}{4}\) bag of coffee beans he gives
them to 2 people how much quantity will each person receives.
Situation 2:
Darren has \(\frac{1}{4}\) shelf of books he gives
them to 2 people how much number of books
will each person receives.
Quantities can be pizzas, candies etc.
Explanation:
Situation 1:
Darren has \(\frac{1}{4}\) bag of coffee beans he gives
them to 2 people how much quantity will each person receives.
Situation 2:
Darren has \(\frac{1}{4}\) shelf of books he gives
them to 2 people how much number of books
will each person receives.
Quantities can be pizzas, candies etc.
Question 2.
Write and solve a word problem that can be modeled by the expression \(\frac{1}{2}\) ÷ 6. Draw a visual model to show the quotient, and then explain what it represents.
A. What word problem can you write that can be modeled by \(\frac{1}{2}\) ÷ 6?
Draw a visual model to show the quotient.
Answer:
Word problem:
Karl has \(\frac{1}{2}\) pizza he divides it among
his 6 freinds how much quantity will each friend will get.
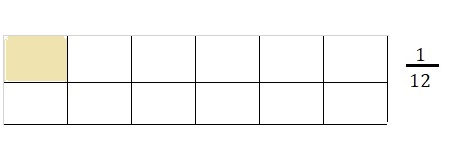
quotient is \(\frac{1}{12}\),
Explanation:
Karl has \(\frac{1}{2}\) pizza he divides it among
his 6 freinds how much quantity will each friend will get.
Drawn a visual model to show the quotient as
\(\frac{1}{12}\) as shown above.
B. Describe the size of each part and what it represents.
Answer:
The size of each part represents each person,
Explanation:
The size of each part represents the quantity how much
each person gets the pizza.
C. Solve your word problem. What does the quotient represent?
Answer:
The quotient represents the quantity of size each receive,
Explantion:
Solving \(\frac{1}{2}\) ÷ 6 =
\(\frac{1}{2}\) X \(\frac{1}{6}\) =
\(\frac{1}{12}\), the quotient \(\frac{1}{12}\)
represents the quantity of pizza size each person will receive.
Turn and Talk How did you decide the type of visual model to use for your problem? Explain.
Answer:
Upon the given situation or problem,
we use tape diagrams, area models, number lines,
Explanation:
Based on the situation or problem we use visuals or
visual model, A math visual model consists of materials
(mostly with pictures or images) to help interpret the numbers.
which ever is suitable for the particular situation can be tape diagrams,
area models, number lines etc.
Step It Out
Question 3.
Look at the visual model.
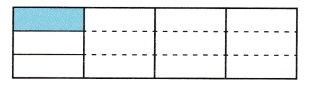
A. Write a division word problem that can be represented by the visual model.
Answer:
Word problem:
Sara has \(\frac{1}{4}\) part of candies which she distributes
among 3 freinds each freind will get how much part of candies,
Explanation:
The word problem that can be represented by the visual model is
Sara has \(\frac{1}{4}\) part of candies which she distributes
among 3 freinds each freind will get how much part of candies.
B. Write a division equation to model your problem. Then solve the problem.
Answer:
Division equation:
\(\frac{1}{4}\) ÷ 3,
quotient = \(\frac{1}{12}\),
Explanation:
The division equation to model the given problem is
\(\frac{1}{4}\) ÷ 3 solving
\(\frac{1}{4}\) X \(\frac{1}{3}\) =
\(\frac{1}{4 X 3}\) = \(\frac{1}{12}\).
Check Understanding
Question 1.
Amy writes a word problem that can be modeled by the expression \(\frac{1}{4}\) ÷ 5. Complete her word problem.

There are _________ truck(s) that need to share the total amount of recycled plastic bottles equally. If there is a collection of _________ ton of plastic bottles, then how much does each truck carry?
Answer:
There are 5 truck(s) that need to share the total
amount of recycled plastic bottles equally.
If there is a collection of \(\frac{1}{4}\) ton of plastic bottles,
then how much does each truck carry?
Explanation:
Given Amy writes a word problem that can be modeled
by the expression \(\frac{1}{4}\) ÷ 5.
Completed her word problem as there are 5 truck(s)
that need to share the total amount of recycled
plastic bottles equally.
If there is a collection of \(\frac{1}{4}\) ton of plastic bottles,
then how much does each truck carry?.
Question 2.
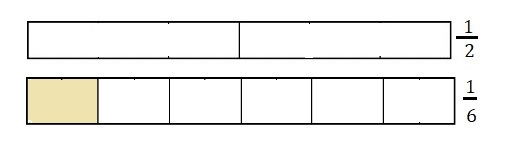
A doctor has \(\frac{1}{2}\) hour to see 3 patients. If the doctor divides the time equally among the patients, how much time will be spent with each patient? Draw a visual model to represent the problem.
Answer:
Time spent with each patient is \(\frac{1}{6}\),
Explanation:
Given a doctor has \(\frac{1}{2}\) hour
to see 3 patients. If the doctor divides the time
equally among the patients, time will be spent with
each patient is \(\frac{1}{2}\) ÷ 3,
\(\frac{1}{2}\) X \(\frac{1}{3}\) =
\(\frac{1}{6}\), Drawn a visual model to
represent the problem as shown above.
On Your Own
Question 3.
Write a word problem that involves a plot of land and a number of different crops that can be modeled by the expression \(\frac{1}{2}\) ÷ 5.

Will the quotient be less than \(\frac{1}{2}\) or greater than \(\frac{1}{2}\). Justify your thinking.
Answer:
Word problem:
A plot of \(\frac{1}{2}\) land has been used to grow
5 different crops how much part of land each crop will get,
quotient will be less than \(\frac{1}{2}\),
Explanation:
Wrote a word problem that involves a plot of land and
a number of different crops that can be modeled by the
expression \(\frac{1}{2}\) ÷ 5 is
Word problem:
A plot of \(\frac{1}{2}\) land has been used to grow
5 different crops how much part of land each crop will get,
The quotient will be less than \(\frac{1}{2}\) as it is
again divided by 5 so it will be divided again into parts
theerefore the quotient will be less than \(\frac{1}{2}\).
Question 4.
Use Tools Write a word problem for the expression \(\frac{1}{5}\) ÷ 4. Then draw a visual model and solve your problem.
Answer:
Word problem:
A wall of \(\frac{1}{5}\) of portion is completed by
4 persons each person has built how much portion of the wall,
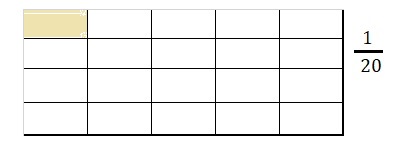
Each person has buitl \(\frac{1}{20}\),
Explanation:
Word problem for the expression \(\frac{1}{5}\) ÷ 4 is
Word problem:
A wall of \(\frac{1}{5}\) of portion is completed by
4 persons each person has built how much portion of the wall,
drawn a visual model as shown above and solving
\(\frac{1}{5}\) ÷ 4 = \(\frac{1}{5}\) X \(\frac{1}{4}\) =
\(\frac{1}{5 X 4}\) = \(\frac{1}{20}\),
therefore each person has buitl \(\frac{1}{20}\).
Question 5.
Attend to Precision Margie writes a word problem for the expression \(\frac{1}{3}\) ÷ 6: “A bottle of mouthwash is \(\frac{1}{3}\) empty. If the remaining amount is divided equally over 6 weeks, what fraction of the bottle is used each week?”
What mistake did she make in her problem?
Answer:
Mistake she made writing the word problem is instead of empty
mouth wah and remaining amount is division,
Explanation:
Given Margie writes a word problem for the
expression \(\frac{1}{3}\) ÷ 6:
“A bottle of mouthwash is \(\frac{1}{3}\) empty.
If the remaining amount is divided equally over 6 weeks,
what fraction of the bottle is used each week?”
The mistake did she make in her problem instead of empty
\(\frac{1}{3}\) and remaining amount is divided among
6 weeks.
Correct her word problem. Then find the answer using a visual model.
Answer:
Correct word problem:
“A bottle of mouthwash is \(\frac{1}{3}\) filled.
If the amount is divided equally over 6 weeks,
what fraction of the bottle is used each week?”,
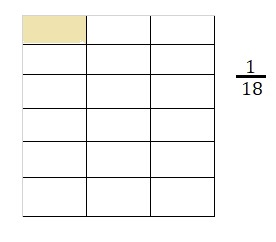
\(\frac{1}{18}\) of the bottle is used each week,
Explanation:
Correct word problem for the expression \(\frac{1}{3}\) ÷ 6 is
“A bottle of mouthwash is \(\frac{1}{3}\) filled.
If the amount is divided equally over 6 weeks,
what fraction of the bottle is used each week?”,
Drawn a visual model as shown above solving
\(\frac{1}{3}\) ÷ 6 = \(\frac{1}{3}\) X \(\frac{1}{6}\) =
\(\frac{1}{3 X 6}\) = \(\frac{1}{18}\),
therefore \(\frac{1}{18}\) of the bottle is used each week.
Question 6.
Model with Mathematics Write a division word problem that can be represented by the visual model. Then write a division equation and solve your problem.
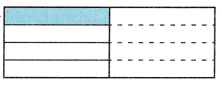
Answer:
Word problem:
“Mary has shared her
\(\frac{1}{2}\) of jam bottle among
4 of her friends, how much portion of the jam
each of friend will get”,
Division equation: \(\frac{1}{2}\) ÷ 4,
Quotient is \(\frac{1}{8}\),
Explanation:
The word problem that can be represented by
the given visual model is “Mary has shared her
\(\frac{1}{2}\) of jam bottle among
4 of her friends, how much portion of the jam
each of friend will get”.
Division equation: \(\frac{1}{2}\) ÷ 4,
Solving \(\frac{1}{2}\) ÷ 4 =
\(\frac{1}{2}\) X \(\frac{1}{4}\) =
\(\frac{1}{2 X 4}\) = \(\frac{1}{8}\).
Quotient is \(\frac{1}{8}\) so each friend
will get \(\frac{1}{8}\) portion of jam.
Question 7.
Open-Ended Consider the expression \(\frac{1}{5}\) ÷ 3.
Write two different word problems that can be represented by this expression.
Answer:
Word problem 1:
“Rosy has \(\frac{1}{5}\) portion of apple juice
with her she distributes among 3 friends how much juice
will each friend will get?”
Word problem 2:
“Three friends finishes \(\frac{1}{5}\) portion of
planting flower plants in a garden, How much does each
one has planted?”,
Explanation:
Considering the expression \(\frac{1}{5}\) ÷ 3.
The two different word problems that can be represented
by this expression is Word problem 1:
“Rosy has \(\frac{1}{5}\) portion of apple juice
with her she distributes among 3 friends how much juice
will each friend will get?”
Word problem 2:
“Three people finishes \(\frac{1}{5}\) portion of
planting flower plants in a garden, How much does each
one has planted?”.
Draw a visual model to represent the problems and then solve.
Answer:
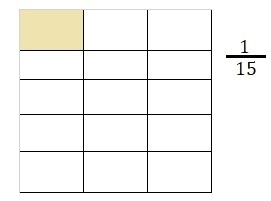
Quotient is \(\frac{1}{15}\),
Explanation:
Drawn a visual model to represent the problems and then solved
\(\frac{1}{5}\) ÷ 3 = \(\frac{1}{5}\) X \(\frac{1}{3}\) =
\(\frac{1}{5 X 3}\) = \(\frac{1}{15}\).
What does the quotient represent in each problem?
Answer:
Problem 1 quotient represents each friend got
\(\frac{1}{15}\) portion of apple juice,
Problem 2 quotient represents each person got
\(\frac{1}{15}\) portion of plants planted,
Explanation:
The quotient is same in both the problems but
it represents differently as in problem 1 quotient
epresents each friend got \(\frac{1}{15}\) portion
of apple juice, In problem 2 quotient represents
each person got \(\frac{1}{15}\) portion of
plants planted,
I’m in a Learning Mindset!
How can I work with others to write word problems?
Answer:
Discuss visualize and write,
Explanation:
While working with others to write the word problems first discuss about the problem situation then visualize come to conculsion then write the word problems.