We included HMH Into Math Grade 5 Answer Key PDF Module 1 Lesson 1 Recognize the 10 to 1 Relationship Among Place-Value Positions to make students experts in learning maths.
HMH Into Math Grade 5 Module 1 Lesson 1 Answer Key Recognize the 10 to 1 Relationship Among Place-Value Positions
I Can describe place-value relationships in multi-digit whole numbers.
Spark Your Learning
On a road trip, Anna and her family stop at a ranch where bales of hay are being weighed. Describe the relationship between the two weights. How can you use the relationship to compare the weights?


Answer:
Given that,
The weights are 50lb and 500lb.
In 50lb the place value of 0 is one’s and the place value of 5 is tens.
In 500lb the place value from the write position is one’s, tens and hundred.
50lb < 500lb
or
500lb > 50lb
Turn and Talk What is another way to describe the relationship between the weights? How can you use that relationship to compare the weights?
Build Understanding
1. Anna’s aunt opens a savings account for her. Anna, her brother, and her aunt all make contributions. The amount of each contribution is shown.

A. Complete the place-value chart to show the amount of money that each person contributes.

Answer:
The contribution of Anna’s aunt is 100 dollars.
The contribution of Ann’s brother is 10 dollars.
The contribution of Anna is 1 dollars.
B. What is the relationship between the amount of money Anna’s aunt contributes and the amount Anna’s brother contributes?
_______________________________
Answer:
Given that,
The amount of money Anna’s aunt contributes is 100 dollars.
The amount of money Anna’s brother contributes is 10 dollars.
Therefore the relationship between Ann’s aunt and Ann’s brother is 100 dollars > 10 dollars or 10 dollars < 100 dollars.
C. How does the position of the digit 2 change when the amount Anna’s brother contributes is multiplied by 10?
_______________________________
Answer:
Given that,
The amount of money Anna’s brother contributes is 10 dollars.
Therefore, the amount Anna’s brother contributes is multiplied by 10 is 10 x 10 = 100.
The digit 2 chances to the hundreds place.
D. What is the relationship between the amount Anna contributes and the amount Anna’s brother contributes?
_______________________________
Answer:
Given that,
The amount of money Anna’s contributes is 1 dollar
The amount of money Anna’s brother contributes is 10 dollars.
Therefore the relationship between Ann’s and Ann’s brother is 10 dollars > 1 dollars or 1 dollars < 10 dollars.
E. How does the position of the digit 2 change when finding ^ of the amount Anna’s brother contributes?
_______________________________
2. A. Complete each column in the table.

B. How does the number of zeros in each number change • in the “10 times as much” column?
- in the “10 times as much” column?
____________________ - in the “A of” column?
____________________ - in the “\(\frac{1}{10}\) of” column?
Answer:
600,000 in the “10 times as much” column.
800 in 1 time as much.
7,000 in the “\(\frac{1}{10}\) of” column.
Turn and Talk Explain how you found the unknown values in each row.
Check Understanding Math Board
Question 1.
There are 60 students on a school bus. One-tenth of the students are in fifth grade. How many fifth graders are there?

____ of 60 students is ____
Answer:
Given,
There are 60 students on a school bus. One-tenth of the students are in fifth grade.
60 × 1/10 = 6
Thus there are 6 fifth graders on a school bus.
Question 2.
When 600 is multiplied by 10, how does the position of the digit 6 change?
____________________
Answer:
600
×10
6000
So, when we multiply 600 by 10 we get 6000.
The position of the digit 6 will change its place to 6 thousand.
Question 3.
What number is 10 times as much as 200? __________
Answer:
200
×10
2000
2000 is 10 times as much as 200.
Question 4.
What number is \(\frac{1}{10}\) of 900,000 ? __________
Answer:
900,000 × \(\frac{1}{10}\) = 90,000
So, 90,000 is \(\frac{1}{10}\) of 900,000.
On Your Own
Question 5.
Use Tools How do you know that 400 is 10 times as much as 40? Show your work.
Answer:
40 × 10 = 400
So, 10 times 40 is 400.
Question 6.
Use the place-value chart to describe how 800,000 and 8,000,000 compare to each other.

Answer:
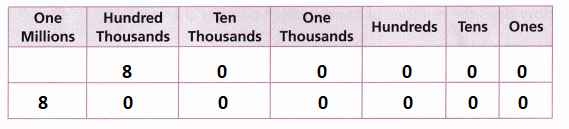
Question 7.
What number is 10 times as much as 5,000? __________
Answer:
5000
×10
50000
So, 50,000 is 10 times as much as 5,000.
Question 8.
What number is \(\frac{1}{10}\) of 900? ____
Answer:
900 × \(\frac{1}{10}\) = 90
90 is \(\frac{1}{10}\) of 900
Question 9.
Attend to Precision Gavin has 30 stickers. Marissa has 300 stickers. Write a sentence that relates the number of stickers Gavin has to the number of stickers Marissa has.

Answer:
Given,
Gavin has 30 stickers. Marissa has 300 stickers.
30 ÷ 300 = 1/10 or 0.1
Question 10.
Open Ended The answer to a place-value question is 50,000. What could be the question?
Answer:
Write the place of digit 5 in the number 56782.
I’m in a Learning Mindset!
How did using a table help me understand the relationship between two place-value positions?
___________________________________________
Answer:
By using the place value table we can easily find the relationship between two place-value positions.