We included HMH Into Math Grade 4 Answer Key PDF Module 21 Lesson 4 Practice with Mixed Measures to make students experts in learning maths.
HMH Into Math Grade 4 Module 21 Lesson 4 Answer Key Practice with Mixed Measures
I Can use my understanding of the relative size of measurement units and more than one operation to solve problems involving length and time.
Step It Out
Question 1.
Ella competes in a mountain bike race and finishes 12 minutes 42 seconds after Lian, who finishes in 58 minutes 43 seconds. Inez finishes 5 minutes 15 seconds after Ella. How long does it take Inez to finish the race?

A. Whose finishing time do you know? What was their time?
Answer:
I know Lian finishing time. Lian finishes the mountain bike race in 58 minutes 43 seconds.
B. How can you use the known time to find Ella’s finishing time?
Answer:
Ella finishes the mountain bike race in 12 minutes 42 seconds after Lian.
Add given Ella’s finishing time with Lian finishing time.
12 minutes 42 seconds + 58 minutes 43 seconds = 70 minutes 85 seconds
Ella’s finishes the mountain bike race in 70 minutes 85 seconds.
C. What is Ella’s finishing time? Regroup if necessary. Show your work.
Answer:
Ella’s finishing time is 70 minutes 85 seconds.
Here we have to regroup seconds as minute and minutes as hour.
1 minute = 60 seconds
1 hour = 60 minutes
Ella’s finishing time 70 minutes 85 seconds is regrouped as 1 hour 11 minutes 25 seconds.
D. How can you find Inez’s finishing time?
Answer:
Inez finishes the mountain bike race in 5 minutes 15 seconds after Ella.
To calculate Inez’s finishing time we have to add given Inez’s finishing time with Ella’s finishing time.
E. What is Inez’s time? Show your work.
Answer:
Inez finishes 5 minutes 15 seconds after Ella.
Add given Inez’s finishing time with Ella finishing time.
5 minutes 15 seconds + 1 hour 11 minutes 25 seconds = 1 hour 16 minutes 40 seconds
Inez’s finishes the mountain bike race in 1 hour 16 minutes 40 seconds.
Turn and Talk What strategies can you use to check your answers?
Answer:
Question 2.
An obstacle course includes three walls and a cargo net. The three walls are 78 centimeters, 78 centimeters, and 1 meter tall. The height of the cargo net is the sum of the heights of the three walls. How tall is the cargo net?

A. What information do you know?
Answer:
I know the heights of the three wall. The three walls height are 78 centimeters, 78 centimeters, and 1 meter tall.
B. What information do you need to find out?
Answer:
I need to find the height of the cargo net.
C. Describe how you can use the known information to solve.
Answer:
The height of the cargo net is the sum of the heights of the three walls. The three walls height are 78 centimeters, 78 centimeters, and 1 meter tall.
1 meter is equal to 100 centimeters
Add all the heights of the three wall.
78 cm + 78 cm + 100 cm = 256 cm
D. The height of the cargo net is _________ centimeters.
Answer:
The height of the cargo net is 256 centimeters.
Question 3.
The start banner for the bike race is 3 feet 10 inches wide. Its length is 8 inches more than three times its width. How many inches long is the start banner?

A. What do you know about the banner?
Answer:
The banner is 3 feet 10 inches wide. Its length is 8 inches more than three times its width.
B. What information do you need to find out?
Answer:
I need to find out the length of the start banner in inches.
C. Find the width of the banner in inches.
3 feet 10 inches = _________ inches
Answer:
We know that 1 feet = 12 inches
3 feet = 12 x 3 = 36 inches
36 inches + 10 inches = 46 inches
So, 3 feet 10 inches is equal to 46 inches.
The width of the banner is 46 inches.
D. Multiply the width in inches by 3. Then add 8 inches.

Answer:

Explanation:
The width 46 inches is multiplied by 3.
46 x 3 = 138 inches
Add 138 inches to 8 inches the sum is equal to 146 inches.
138 + 8 = 146 inches
E. How long is the start banner?
Answer:
The start banner is 146 inches long.
Check Understanding
Question 1.
Ella rode her bike for a total of 6 hours 48 minutes. Lian rode 1 hour 24 minutes less than Ella. Inez rode 1 hour 6 minutes more than Lian. How long did Inez ride?
Answer:
Ella rode her bike for a total of 6 hours 48 minutes.
Lian rode 1 hour 24 minutes less than Ella.
To calculate Lian rode time we need to perform subtraction operation. Subtract Lian rode time from Ella rode time.
6 hours 48 minutes – 1 hour 24 minutes = 5 hours 24 minutes
Lian rode her bike for 5 hours 24 minutes.
Inez rode 1 hour 6 minutes more than Lian.
To calculate Inez rode time we need to perform addition operation. Add Lian rode time with given Inez rode time.
5 hours 24 minutes + 1 hour 6 minutes = 6 hours 30 minutes
Inez ride bike for 6 hours 30 minutes.
Question 2.
The first obstacle in an obstacle course is 5 feet 3 inches long. The second obstacle is 15 inches shorter than the first obstacle. How long was the second obstacle in the obstacle course?
Answer:
The first obstacle in an obstacle course is 5 feet 3 inches long.
The second obstacle is 15 inches shorter than the first obstacle.
Here we have to convert 5 feet into inches because the second obstacle is in inches.
We know that 1 feet is equal to 12 inches.
Multiply 5 with 12 the product is equal to 60 inches.
5 x 12= 60 inches
Add 60 inches with 3 inches the sum is equal to 63 inches which is first obstacle.
To calculate the second obstacle we have to subtract given second obstacle from the first obstacle.
63 inches – 15 inches = 48 inches
The second obstacle in the obstacle course is 48 inches or 4 feet(12 x 4 = 48).
Question 3.
The first loop of the bike race course is 3 kilometers 540 meters. The second loop is 720 meters more than twice the length of the first loop. How long is the second loop in meters?
Answer:
The first loop of the bike race course is 3 kilometers 540 meters.
The second loop is 720 meters more than twice the length of the first loop.
3 kilometers 540 meters + 3 kilometers 540 meters = 6 kilometers 1080 meters or 7 kilometers 80 meters
After adding 720 meters more than twice the length of the first loop is equal to 7 kilometers 800 meters.
On Your Own
Question 4.
Reason Wesley competes in a swimming race and finishes 22 seconds after Timothy, who has a time of 7 minutes 50 seconds. Aaron finishes 14 seconds before Wesley. How long does it take Aaron to finish the race? Show all your solution steps.
Answer:
Timothy finishes the race in 7 minutes 50 seconds.
Wesley competes in a swimming race and finishes 22 seconds after Timothy.
Add Wesley given finishing time to Timothy finishing time.
7 minutes 50 seconds + 22 seconds = 7 minutes 72 seconds
Wesley finishes the race in 7 minutes 72 seconds.
Aaron finishes 14 seconds before Wesley.
Subtract Aaron given finishing time from Wesley finishing time.
7 minutes 72 seconds – 14 seconds = 7 minutes 58 seconds
Aaron took 7 minutes 58 seconds to finish the race
Question 5.
Attend to Precision A mountain bike club clears 23 yards on a trail at the park. Stacy clears 7 yards 2 feet of the trail. Ricardo clears 22 feet of the trail. How much of the trail was cleared by the rest of the club?

Answer:
A mountain bike club clears 23 yards on a trail at the park.
Stacy clears 7 yards 2 feet of the trail.
Ricardo clears 22 feet of the trail. Convert 22 feet in to yards. We know that 1 yard is equal to 3 feet.
7 x 3 = 21 feet
22 feet – 21 feet = 1 feet
22 feet can be written as 7 yards 1 feet.
Ricardo clears 7 yards 1 feet of the trail.
7 yards 2 feet + 7 yards 1 feet = 15 yards
Both Stacy and Ricardo clears 15 yards of the trail.
To calculate the trail cleared by the rest of the club we have to subtract the trail cleared by both Stacy and Ricardo form the mountain bike club clears the trail at the park.
23 yards – 15 yards = 8 yards
8 yards of the trail was cleared by the rest of the club.
Question 6.
Reason Elizabeth wants to build 4 picture frames for her paintings. She has 6 feet 8 inches of wood to use. If she uses 2 feet 2 inches of wood for the first frame, how much wood can she use for each of the other 3 equal-sized frames? Explain.

Answer:
Elizabeth wants to build 4 picture frames for her paintings. She has 6 feet 8 inches of wood to use.
She used 2 feet 2 inches of wood for the first frame.
Subtract 2 feet 2 inches from 6 feet 8 inches the difference is equal to 4 feet 6 inches. First subtract inches and subtract feet.
6 feet 8 inches – 2 feet 2 inches = 4 feet 6 inches
Now, She has 4 feet 6 inches of wood to use for each of the other 3 equal-sized frames.
Convert 4 feet 6 inches into inches. We know that 1 feet is equal to 12 inches.
4 x 12 = 48 inches
48 inches + 6 inches = 54 inches
4 feet 6 inches is equal to 54 inches.
Divide 54 by 3 the result is equal to 18 inches.
She can use 18 inches or 1 feet 6 inches for each of the other 3 equal-sized frames.
Question 7.
Use Structure The express train leaves the downtown station at 9:22:45 a.m. The train travels for 1 hour 52 minutes 30 seconds and arrives at College Park Station. The train stays at College Park Station for 3 minutes 55 seconds. At what time does the express train leave College Park Station? Show all your solution steps.
Answer:
The express train leaves the downtown station at 9:22:45 a.m.
The train travels for 1 hour 52 minutes 30 seconds and arrives at College Park Station.
To calculate at what time the train arrived at College Park Station. We have to add start time with elapsed time then we get the end time.
9 hours 22 minutes 45 seconds + 1 hour 52 minutes 30 seconds = 10 hours 74 minutes 75 seconds
Here, we have to regroup the seconds as minutes and minutes as hours. We know that 1 minute is equal to 60 seconds and 1 hour is equal to 60 minutes. The time 10 hours 74 minutes 75 seconds is regrouped as 11 hours 15 minutes 15 seconds.
The express train arrived College Park Station at 11:15:15 a.m.
The train stays at College Park Station for 3 minutes 55 seconds.
11 hours 15 minutes 15 minutes + 3 minutes + 55 seconds = 11 hours 18 minutes 70 seconds
Regroup the seconds as minutes we know that 1 minute is equal to 60 seconds. The time 11 hours 18 minutes 70 seconds is regrouped as 11 hours 19 minutes 10 seconds.
The express train leaves College Park Station at 11:19:10 a.m.
Question 8.
Attend to Precision Emilio measures the distances that a pair of tortoises crawled in 10 minutes. The distance each tortoise crawled is shown. Which tortoise crawled farther, and by how much?
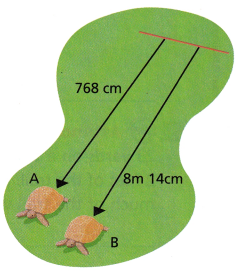
Answer:
Emilio measures the distances that a pair of tortoises crawled in 10 minutes.
Tortoise A crawled the distance of 768 cm.
Tortoise B crawled the distance of 8 m14 cm.
We know that 1 meter is equal to 100 centimeters.
Convert 8 m 14 cm into centimeters.
8 x 1000 = 8,000 cm
8,000 cm + 14 cm = 8,014 cm
Tortoise B crawled the distance of 8,014 cm.
Subtract 768 cm from 8,014 cm the difference is 7,246 cm.
8,014 cm – 768 cm = 7,246 cm
Tortoise B crawled farther by 7,246 cm or 7 m 246 cm.