We included HMH Into Math Grade 4 Answer Key PDF Module 2 Lesson 4 Apply the Perimeter Formula for Rectangles to make students experts in learning maths.
HMH Into Math Grade 4 Module 2 Lesson 4 Answer Key Apply the Perimeter Formula for Rectangles
I Can apply the perimeter formula to find the perimeter of a rectangle.
Connect to Vocabulary
A formula is a group of mathematical symbols that express a relationship or a way to solve a problem.
Step It Out
1. Tom and Mary drew plans for a rectangular dog park in their neighborhood. How many meters of fencing would they need to go around the dog park?
The formula below can be used to find the perimeter of a rectangle.
Perimeter = P = l + w + l + w
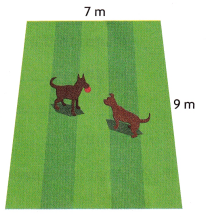
A. What are the values for l and w ?
l = ___meters
w = ___ meters
Explanation:
l = 9 meters
w = 7 meters
B. Replace l and w in the formula for perimeter with their values.
P = ___ + ___ + ___ + ___
Explanation:
p = 9 + 7 + 9 + 7
p = 18 + 14
p = 32
C. Calculate to find the value of P.
P = ____
p = 32
D. Solve the problem.
Tom and Mary need ___ meters of fencing.
Explanation:
Tom and Mary need 32 meters of fencing.
Turn and Talk How could you write the formula for the perimeter of a rectangle and the formula for the perimeter of a square using multiplication?
Explanation:
perimeter of a rectangle = 2 (l + w)
perimeter of a square = 4 x a = 4a
a = side
Step It Out
2. Sandy wants to put a rectangular bench by the fountain. She wants the length to be 3 times the width. What is the perimeter of the bench top?
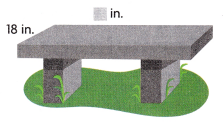
A. What is width of the bench? ___ inch
Explanation:
the given width is 18
and the length is 3 times the width
18 x 3 = 54
B. Use what the problem tells you about how the length relates to the width and find the length of the bench.
length = __ × width
= ___ × ___ = ___
length = ___ inches
Explanation:
length = 3 × width
= 3 × 18 = 54
length = 54 inches
C. What is the perimeter of the bench top? Show your work.
________________________________
perimeter of the bench top = 2 (l + w)
= 2( 18 + 54)
= 2 x 72
= 144
Turn and Talk How could you find the length if you were only given the perimeter and the width of a rectangle?
Explanation:
In the same way, if the perimeter and the width are known, the length can be calculated using the formula: Length(L) = P/2 – w. Where P = perimeter of the rectangle; and w = width of the rectangle.
Check Understanding Math Board
Question 1.
Eric wants to buy a string of lights to go around his window. His window has a width of 4 feet and a length that is 2 feet longer than its width. How many feet of lights should Eric buy?
Answer:
Eric should buy 24 feet of lights
Explanation:
His window has a width of 4 feet
length that is 2 feet longer than its width
2 x 4 = 8
perimeter = 2 (l + w)
2 (4 + 8)
= 2 x 12
= 24
Question 2.
A fence can prevent animals from eating the vegetable garden. What is the least amount of fencing needed to surround the garden?
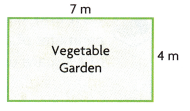
Answer:
22 meters
Explanation:
perimeter = 2 (l + w)
= 2 (7 + 4)
= 2 x 11
= 22 is the least amount of fencing needed to surround the garden
On Your Own
Question 3.
Use Structure The new state park will have a rectangular shape with a length of 6 miles and a width of 3 miles. What is the perimeter of the park?
Answer:
= 18 miles
Explanation:
perimeter = 2 (l + w)
= 2 (6 + 3)
= 2 x 9
= 18 is the perimeter of the park
Question 4.
Use Structure Zach is training to run a marathon. His practice route is the shape of a square that is 8 kilometers in one direction. How far does Zach run in his practice route?
Answer:
= 32 kilometers
Explanation:
side = 8
perimeter of a square= 4 x side
= 4 x 8
= 32 kilometers far that Zach run in his practice route
Question 5.
Reason Ashley wants to build a new rectangular pen for her pet rabbit. She knows the perimeter of the new pen will be 40 feet. She also knows that the length can only be 12 feet. What is the width of her new rabbit pen? Explain your thinking.
Answer:
the width of her new rabbit pen = 8 feet
Explanation:
40 = 2 (12 + w)
40 = 24 + 2w
2w = 40 – 24
2w = 16
w = 16 ÷ 2
w = 8
Question 6.
The dimensions for a new wildflower garden are shown. A rope will be placed around the perimeter of the rectangular garden until the seeds have sprouted and bloomed. What is the least amount of rope needed to go around the perimeter of the garden?

Answer:
46 feet is the least amount of rope needed to go around the perimeter of the garden
Explanation:
perimeter of the garden = 2 (l + w)
p = 2 (11 + 12)
p = 2 x 23
p = 46
Question 7.
Attend to Precision Find the perimeter of a rectangle if the width is 10 inches and the length is 2 times the width. Explain your thinking.
Answer:
perimeter of a rectangle = 60 meters
Explanation:
width is 10 inches and the length is 2 times the width
2 x 10 = 20
length = 20
p = 2(l + w)
p = 2(10 + 20 )
p = 2 x 30
p = 60
On Your Own
Question 8.
Use Structure Carson is trying out for the football team. He practices drills in a small rectangular field that is 10 yards wide and 11 yards long. What is the perimeter of the field that Carson practices on?
Answer:
42 yards is the perimeter of the field that Carson practices on
Explanation:
perimeter of the field
p = 2(l + w)
p = 2 (10 + 11)
p = 2 x 21
p = 42
Question 9.
Model with Mathematics The school wants to build a small dance floor in their auditorium. The perimeter of the new dance floor will be 44 yards. The length can only be 12 yards. What is the width of their new dance floor? Write an equation and show how you solved the problem.
Answer:
10 yards is the width of their new dance floor
Explanation:
p = 44 yards that is given
l = 12 yards given
w = n
we have to find the width
p = 2(l + w)
44 = 2 (12 + w)
44 = 24 + 2w
2w = 44 – 24
2w = 20
w = 20 ÷ 2
w = 10
Question 10.
Use Structure The dimensions for Diane’s rectangular vegetable garden are shown. She wants to put a border around the garden. How many feet of border does Diane need?

Answer:
30 feet of border that Diane need
Explanation:
p = 2(l + w)
p = 2 (9 + 6)
p = 2 x 15
p = 30
Question 11.
Reason Find the perimeter of a rectangle if the width is 6 centimeters and the length is 5 centimeters longer than the width. Explain your thinking.
Answer:
perimeter of a rectangle = 22 centimeters
Explanation:
p = 2(l + w)
width is 6 centimeters
length is 5 centimeters
p = 2 (5 + 6)
p = 2 x 11
p = 22 centimeters