We included HMH Into Math Grade 4 Answer Key PDF Module 16 Lesson 2 Find Multiples of Fractions to make students experts in learning maths.
HMH Into Math Grade 4 Module 16 Lesson 2 Answer Key Find Multiples of Fractions
I Can represent the product of a whole number and a fraction as the product of a whole number and a unit fraction.
Spark Your Learning
Karl participates on a youth wheelchair- basketball team. The team practices 3 times a week after school for \(\frac{3}{4}\) hour.

How can you use multiplication to find how long Karl’s basketball team practices each week?
Show your thinking.
Answer:
3\(\frac{3}{4}\) hour = \(\frac{9}{4}\) hour
Explanation:
The team practices 3 times a week after school for \(\frac{3}{4}\) hour.
\(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) = \(\frac{9}{4}\)
Turn and Talk How does your method of solving the problem compare with your classmates’ methods?
Answer:
Answer may vary.
Problem solving methods help every one in the class.
Explanation:
When we compare with the classmates method, I used unit faction method.
Build Understanding
Question 1.
Jesse is part of a snowboarding team. It takes \(\frac{3}{10}\) hour to take the ski lift to the top of the mountain. While preparing for a competition, Jesse takes the lift to the top of the mountain 4 times.

How much time does Jesse spend on the ski lift?
Represent the problem using fraction strips. Draw a visual representation of your fraction strips and solve.
Answer:

A. How can you write an equation using a unit fraction to show how much time it takes for one ski lift ride?
Answer:
3\(\frac{1}{10}\) = \(\frac{3}{10}\)
B. How can you use the equation for one ski lift ride to write another equation to model the time for four ski lift rides?
Answer:
12\(\frac{1}{10}\) = \(\frac{12}{10}\)
C. Jesse is on the ski lift for __________ hours.
Answer:
\(\frac{12}{10}\)
Explanation:
It takes \(\frac{3}{10}\) hour to take the ski lift to the top of the mountain.
Jesse takes the lift to the top of the mountain 4 times.
4\(\frac{3}{10}\) = \(\frac{12}{10}\)
Turn and Talk How can thinking about 4 groups of 3 tenths help you solve the problem?
Answer:
4\(\frac{3}{10}\) = \(\frac{12}{10}\)

Explanation:
Each group is divided into 3 tenths.
4\(\frac{3}{10}\) = \(\frac{12}{10}\)
Question 2.
Ulrich is training for a race. He runs without stopping for \(\frac{2}{3}\) hour each day for 4 days. How many hours does Ulrich train altogether?

A. Use the number line to show how many hours Ulrich trains by finding multiples of 4.
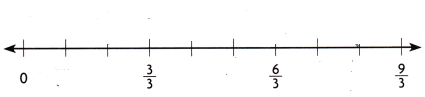
Answer:
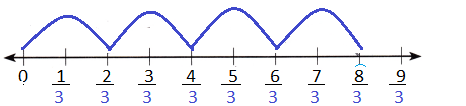
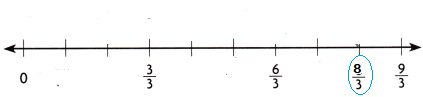
B. What multiplication equation can you write to model the problem?
Answer:
4\(\frac{2}{3}\) hours = \(\frac{8}{3}\) hours
C. How long does Ulrich train?
Answer:
\(\frac{8}{3}\) hours
D. How could you write an equation to model this problem using a unit fraction. Explain your thinking.
Answer:
\(\frac{8}{3}\) hours = 8\(\frac{1}{3}\) hours
Explanation:
Ulrich runs without stopping for \(\frac{2}{3}\) hour each day for 4 days.
Number of hours Ulrich train runs altogether = 4\(\frac{2}{3}\)
= \(\frac{8}{3}\) hours
Check Understanding
Question 1.
Gracie is in charge of running the timing clock at a race. The time clock uses batteries that weigh pound each. If the timing clock uses 4 batteries, what is the weight of all the batteries?
Answer:
4\(\frac{3}{4}\) = \(\frac{12}{4}\)
Explanation:
Gracie is in charge of running the timing clock at a race.
The time clock uses batteries that weigh pound each.
If the timing clock uses 4 batteries,
the weight of all the batteries = 4\(\frac{3}{4}\) = \(\frac{12}{4}\)
Question 2.
Find the product. 5 × \(\frac{3}{4}\).
Answer:
\(\frac{15}{4}\)
Explanation:
To find the products multiply 5 and \(\frac{3}{4}\)
= \(\frac{15}{4}\)
Question 3.
Write the first 4 multiples of \(\frac{3}{8}\).
Answer:
\(\frac{3}{8}\); \(\frac{6}{8}\); \(\frac{9}{8}\); \(\frac{12}{8}\)
Explanation:
Multiples are the numbers, when we multiply a certain number by an integer.
On Your Own
Question 4.
Reason Sam is building a table. He needs to cut 4 pieces of wood that are each \(\frac{5}{6}\) yard long. What is the length of wood Sam needs for the table?
Answer:
4\(\frac{5}{6}\) = \(\frac{20}{6}\)
Explanation:
Sam needs to cut 4 pieces of wood that are each \(\frac{5}{6}\) yard long.
Total length of wood Sam needs for the table = 4\(\frac{5}{6}\) = \(\frac{20}{6}\)
Question 5.
Use Tools Yvonne is making baskets to help raise money to feed the homeless. She includes \(\frac{1}{2}\) pound of pecans in each basket. If she makes 5 baskets, how many pounds of pecans does she use? Use the number line to represent how many pounds of pecans Yvonne uses, and then answer the question.
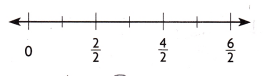
Answer:
5\(\frac{1}{2}\) = \(\frac{5}{2}\) = 2 \(\frac{1}{2}\)
Explanation:
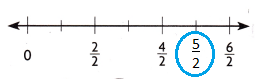
Yvonne includes \(\frac{1}{2}\) pound of pecans in each basket.
If she makes 5 baskets,
Total pounds of pecans she use = 5\(\frac{1}{2}\) = \(\frac{5}{2}\)
Question 6.
Reason Tammi trains dogs. She feeds each dog \(\frac{2}{3}\) pound of food every day. If she is training 5 dogs, how much food does she need for one day?
Answer:
5\(\frac{2}{3}\) = \(\frac{10}{3}\)
Explanation:
Tammi feeds each dog \(\frac{2}{3}\) pound of food every day.
If she is training 5 dogs,
Total food she need for one day = 5\(\frac{2}{3}\) = \(\frac{10}{3}\)
Question 7.
6 × \(\frac{3}{10}\) = _______ × \(\frac{1}{10}\) = _______
Answer:
18\(\frac{1}{10}\) = \(\frac{18}{10}\)
Explanation:
Convert the mixed fraction into improper fraction.
6 × \(\frac{3}{10}\) = 18\(\frac{1}{10}\)
= \(\frac{18}{10}\)
Question 8.
3 × \(\frac{7}{8}\) = _______ × \(\frac{1}{8}\) = _______
Answer:
21\(\frac{1}{8}\) = \(\frac{21}{8}\)
Explanation:
Convert the mixed fraction into improper fraction.
3 × \(\frac{7}{8}\) = 21\(\frac{1}{8}\)
= \(\frac{21}{8}\)
Write the first 4 multiples of the fraction.
Question 9.
\(\frac{7}{10}\): ___________
Answer:
\(\frac{7}{10}\):\(\frac{14}{10}\):\(\frac{21}{10}\):\(\frac{28}{10}\)
Explanation:
Multiples of a fraction are the same as multiples of an integer.
Multiples are the numbers we get, when we multiply a certain number by an integer.
\(\frac{7}{10}\):\(\frac{14}{10}\):\(\frac{21}{10}\):\(\frac{28}{10}\)
Question 10.
\(\frac{3}{12}\): ____________
Answer:
\(\frac{3}{12}\):\(\frac{6}{12}\):\(\frac{9}{12}\):\(\frac{12}{12}\)
Explanation:
Multiples of a fraction are the same as multiples of an integer.
Multiples are the numbers we get, when we multiply a certain number by an integer.
\(\frac{3}{12}\):\(\frac{6}{12}\):\(\frac{9}{12}\):\(\frac{12}{12}\)
I’m in a Learning Mindset!
What strategies for finding multiples of fractions did I share with my classmates?
Answer:
Multiply the numerators and the denominators.
If needed, simplify or reduce the fraction.
Explanation:
The first step when multiplying fractions is to multiply the two numerators.
The second step is to multiply the two denominators.
The fractions can also be simplified before multiplying by factoring.
Finally, simplify the new fractions.