We included HMH Into Math Grade 4 Answer Key PDF Module 15 Lesson 3 Add and Subtract Mixed Numbers to Solve Problems to make students experts in learning maths.
HMH Into Math Grade 4 Module 15 Lesson 3 Answer Key Add and Subtract Mixed Numbers to Solve Problems
I Can use visual models and equations to add and subtract mixed numbers with like denominators.
Spark Your Learning
A diner serves fresh bread with certain meals. At the end of the night, there are 1\(\frac{3}{4}\) loaves of whole wheat bread left and 1\(\frac{2}{4}\) loaves of white bread left. How many loaves of bread does the diner have at the end of the night?

Draw a visual model to help you solve the problem.
Answer:
3\(\frac{1}{4}\)
Visual model

Explanation:
whole wheat bread 1\(\frac{3}{4}\) + white wheat bread 1\(\frac{2}{4}\)
= \(\frac{7}{4}\) + \(\frac{6}{4}\)
= \(\frac{6+7}{4}\)
= \(\frac{13}{4}\)
= 3\(\frac{1}{4}\)
Turn and Talk How could you find the solution without using a visual model? Write an equation to model the problem.
Answer:
3\(\frac{1}{4}\)
Explanation:
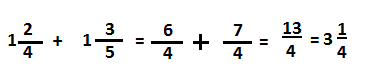
Build Understanding
Question 1.
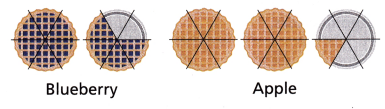
A diner sells pie by the slice. At the end of the night, they have the following slices left. How much pie is left?
Show your work.
Answer:
1\(\frac{1}{6}\)
Explanation:
Blueberry + Apple
1\(\frac{4}{6}\) + 2\(\frac{1}{6}\)
= \(\frac{10}{6}\) + \(\frac{13}{6}\)
= \(\frac{10+13}{6}\)
= \(\frac{23}{6}\)
= 3 \(\frac{5}{6}\)
Total slices of pie = 6 x 5 = 30
= \(\frac{30 – 23}{6}\) = \(\frac{7}{6}\)
= 1\(\frac{1}{6}\)
A. How many wholes do you have? What fraction represents the remaining slices?
Answer:
3 wholes
1\(\frac{1}{6}\) fraction slices
Explanation:
1\(\frac{4}{6}\) + 2\(\frac{1}{6}\)
= \(\frac{10}{6}\) + \(\frac{13}{6}\)
=\(\frac{10 + 13}{6}\)
=\(\frac{23}{6}\)
=3 \(\frac{5}{6}\) – 30
= 1\(\frac{1}{6}\)
B. Write an equation to model the problem.
Answer:
1\(\frac{4}{6}\) + 2\(\frac{1}{6}\)
Explanation:
1\(\frac{4}{6}\) + 2\(\frac{1}{6}\)
= \(\frac{10}{6}\) + \(\frac{13}{6}\)
=\(\frac{23}{6}\)
C. There are __________ pies left.
Answer:
7 pies left
Explanation:
1\(\frac{4}{6}\) + 2\(\frac{1}{6}\)
= \(\frac{10}{6}\) + \(\frac{13}{6}\)
=\(\frac{23}{6}\) – 30
= \(\frac{7}{6}\) = 1\(\frac{1}{6}\)
Turn and Talk How do you know if you need to rename a mixed number in your answer?
Answer:
If the numerator is more than the denominator the fraction is converted into mixed fraction.
Explanation:
By seeing the improper fraction,
for example;
\(\frac{23}{6}\) = 3\(\frac{5}{6}\)
Step It Out
Question 2.
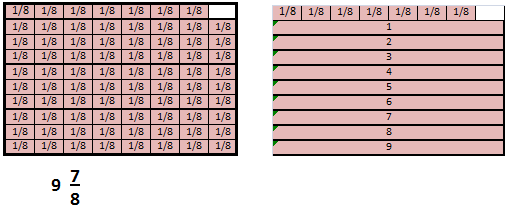
At the start of the day, the diner has this bag of potatoes. During breakfast, they serve 8\(\frac{4}{8}\) pounds of potatoes. How many pounds of potatoes remain?

A. Draw a visual model of the number of potatoes they have at the beginning of the day.
Answer:
9 \(\frac{7}{8}\)
B. Update your drawing to show the potatoes used during the day.
Answer:
1\(\frac{3}{8}\)
Explanation:
9 \(\frac{7}{8}\) – 8 \(\frac{4}{8}\)
= \(\frac{79}{8}\) – \(\frac{68}{8}\)
= \(\frac{79 – 68}{8}\)
= \(\frac{11}{8}\)
= 1\(\frac{3}{8}\)
one whole and \(\frac{3}{8}\) fraction
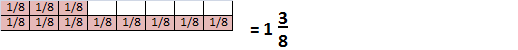
C. Model the problem with an equation and record what is remaining in the drawing as the solution.
There are ___________ pounds of potatoes left after breakfast.
Answer:
1\(\frac{3}{8}\) pounds of potatoes left after breakfast
Explanation:
9 \(\frac{7}{8}\) – 8 \(\frac{4}{8}\)
= \(\frac{79}{8}\) – \(\frac{68}{8}\)
= \(\frac{79 – 68}{8}\)
= \(\frac{11}{8}\)
= 1\(\frac{3}{8}\)
Turn and Talk How could you solve this problem without drawing a visual representation?
Answer:
By subtracting the given fractions
9 \(\frac{7}{8}\) – 8 \(\frac{4}{8}\)
Explanation:
9 \(\frac{7}{8}\) – 8 \(\frac{4}{8}\)
= \(\frac{79}{8}\) – \(\frac{68}{8}\)
= \(\frac{79 – 68}{8}\)
= \(\frac{11}{8}\)
= 1\(\frac{3}{8}\)
Question 3.
The diner has 2\(\frac{3}{8}\) pounds of cheddar cheese and 1\(\frac{7}{8}\) pounds of mozzarella cheese. How many pounds of cheese does the diner have?

A. Draw a picture to help you visualize the problem.
Answer:
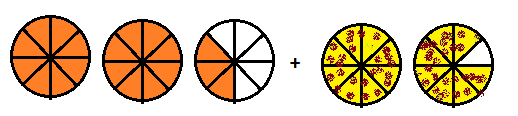
Explanation:
1 whole is of 8 slices,
2\(\frac{3}{8}\) pounds of cheddar cheese and
1\(\frac{7}{8}\) pounds of mozzarella cheese.
Total pounds of cheese does the diner have = 4\(\frac{2}{8}\)
B. Write an equation to model the problem. Use c to represent the total amount of cheese.
Answer:
4\(\frac{2}{8}\)
Explanation:
2\(\frac{3}{8}\) + 1\(\frac{7}{8}\)
= \(\frac{19}{8}\) + \(\frac{15}{8}\)
= \(\frac{19 + 15}{8}\)
= \(\frac{34}{8}\)
= 4\(\frac{2}{8}\)
C. To find the value of c, add the fractional parts of the mixed numbers, and then add the whole number parts.
\(\frac{3}{8}\) + \(\frac{7}{8}\) = ________
2 + 1 = _________
Answer:
4\(\frac{2}{8}\)
Explanation:
\(\frac{3}{8}\) + \(\frac{7}{8}\) = \(\frac{10}{8}\) = 1\(\frac{2}{8}\)
2 + 1 =3
D. Write the value of c as a mixed number. Rename if necessary so the fractional part is less than 1. Show your work.
Answer:
\(\frac{2}{8}\) = =\(\frac{1}{4}\) = 0.25
Explanation:
C = 2\(\frac{3}{8}\) + 1\(\frac{7}{8}\)
= \(\frac{19}{8}\) + \(\frac{15}{8}\)
= \(\frac{19 + 15}{8}\)
=\(\frac{34}{8}\)
= 4\(\frac{2}{8}\)
the fractional part is less than 1
\(\frac{2}{8}\) = \(\frac{1}{4}\) = 0.25
Check Understanding
Question 1.
Basketball practice lasts 2\(\frac{6}{12}\) hours on Monday and 1\(\frac{5}{12}\) hours on Wednesday. How many hours does practice last over both days? How much longer is practice on Monday than on Wednesday?
Answer:
Number of practice over both hours = 3\(\frac{11}{12}\)
Number of hours longer on Monday than on Wednesday = 1\(\frac{1}{12}\)
Explanation:
Basket ball practice on Monday and on Wednesday = 2\(\frac{6}{12}\) + 1\(\frac{5}{12}\)
= \(\frac{30}{12}\) + \(\frac{17}{12}\)
= \(\frac{47}{12}\)
= 3\(\frac{11}{12}\)
Monday practice is much longer than on Wednesday
= 2\(\frac{6}{12}\) – 1\(\frac{5}{12}\)
= \(\frac{30}{12}\) – \(\frac{17}{12}\)
= \(\frac{30 – 17}{12}\)
= \(\frac{13}{12}\)
= 1\(\frac{1}{12}\)
= 1\(\frac{1}{12}\)
On Your Own
Question 2.
Use Tools Isabel has 2\(\frac{5}{6}\) hours free to read and play outside. If she spends 1\(\frac{3}{6}\) hours reading, how long does she have to play outside? Represent the situation with a visual fraction model and an equation.
Answer:
1\(\frac{2}{6}\)
Explanation:
Isabel has 2\(\frac{5}{6}\)hours to read
If he spends 1\(\frac{3}{6}\) hours on reading,
Total ours she play out side = 2\(\frac{5}{6}\) – 1\(\frac{3}{6}\)
=\(\frac{17}{6}\) – \(\frac{9}{6}\)
= \(\frac{17 – 9}{6}\)
= \(\frac{8}{6}\)
= 1\(\frac{2}{6}\)
Question 3.
Reason There are 10\(\frac{5}{8}\) cups of dog food in a bag. Alton feeds his dog \(\frac{3}{8}\) cup of food every day. How many cups of food are left in the bag after 4 days? Show your work.
Answer:
6\(\frac{2}{8}\)
Explanation:
There are 10\(\frac{5}{8}\) cups of dog food in a bag.
Alton feeds his dog \(\frac{3}{8}\) cup of food every day,
Total cups of food left in the bag after 4 days,
10\(\frac{5}{8}\) – 4\(\frac{3}{8}\)
= \(\frac{85}{8}\) – \(\frac{35}{8}\)
= \(\frac{50}{8}\) = 6\(\frac{2}{8}\)
Question 4.
Ms. Goldberg rides the train for 1\(\frac{1}{12}\) hours to get to work. Her train ride home from work takes 1\(\frac{3}{12}\) hours because the train makes more stops. How many hours does Ms. Goldberg spend on the train in 1 day? In 3 days?
Answer:
1 day = 2\(\frac{4}{12}\)
3 days = 5\(\frac{4}{12}\)
Explanation:
Ms. Goldberg rides the train for 1\(\frac{1}{12}\) hours to get to work.
Her train ride home from work takes 1\(\frac{3}{12}\) hours.
Total hours Ms. Goldberg spend on the train in 1 day,
= 1\(\frac{1}{12}\) + 1\(\frac{3}{12}\)
= \(\frac{13}{12}\) + 1\(\frac{15}{12}\)
= \(\frac{28}{12}\) = 2\(\frac{4}{12}\)
In 3 days = 3\(\frac{28}{12}\) = \(\frac{64}{12}\)
= 5\(\frac{4}{12}\)
Question 5.
Attend to Precision Kyra has 1\(\frac{3}{8}\) pounds of clay. How much clay must she buy to have 2\(\frac{7}{8}\) pounds of clay to make a vase?

Answer:
1\(\frac{4}{8}\)
Explanation:
Kyra has 1\(\frac{3}{8}\) pounds of clay.
Total clay she must buy to have 2\(\frac{7}{8}\) pounds of clay to make a vase,
= 2\(\frac{7}{8}\) – 1\(\frac{3}{8}\)
= \(\frac{23}{8}\) – \(\frac{11}{8}\)
= \(\frac{12}{8}\) = 1\(\frac{4}{8}\)
Find the sum. Write your answer as a mixed number.
Question 6.
1\(\frac{9}{10}\) + 1\(\frac{8}{10}\) = ____________
Answer:
3\(\frac{7}{10}\)
Explanation:
1\(\frac{9}{10}\) + 1\(\frac{8}{10}\)
= \(\frac{19}{10}\) + \(\frac{18}{10}\)
= \(\frac{37}{10}\) = 3\(\frac{7}{10}\)
Question 7.
3\(\frac{1}{4}\) + 1\(\frac{2}{4}\) = ____________
Answer:
4\(\frac{3}{4}\)
Explanation:
3\(\frac{1}{4}\) + 1\(\frac{2}{4}\)
= \(\frac{13}{4}\) + \(\frac{6}{4}\)
= \(\frac{19}{4}\) = 4\(\frac{3}{4}\)
Question 8.
\(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) = ___________
Answer:
2\(\frac{3}{6}\)
Explanation:
\(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\)
= \(\frac{15}{6}\) = 2\(\frac{3}{6}\)
Question 9.
2\(\frac{5}{8}\) + 1\(\frac{7}{8}\) = ____________
Answer:
4\(\frac{4}{8}\)
Explanation:
2\(\frac{5}{8}\) + 1\(\frac{7}{8}\)
= \(\frac{21}{8}\) + \(\frac{15}{8}\)
= \(\frac{36}{8}\) = 4\(\frac{4}{8}\)
Question 10.
Open-ended Write and solve a subtraction word problem to match this visual fraction model. Write an equation to represent your problem.
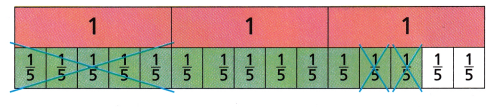
Answer:
1\(\frac{1}{5}\)
Cat use to drink 2\(\frac{3}{5}\) cups of milk daily but on that day it drank 1\(\frac{2}{5}\) milk only.
How much milk is left?
Explanation:
2\(\frac{3}{5}\) – 1\(\frac{2}{5}\)
=\(\frac{13}{5}\) – \(\frac{7}{5}\)
=\(\frac{13 – 7}{5}\)
=\(\frac{6}{5}\)
=1\(\frac{1}{5}\)
Question 11.
Reason Jana has 3 bags of dried fruit. Each bag has 1\(\frac{4}{8}\) cups in it. How many cups of dried fruit does Jana have?
Answer:
4\(\frac{4}{8}\) cups
Explanation:
Jana has 3 bags of dried fruit.
Each bag has 1\(\frac{4}{8}\) cups in it.
Convert mixed number to improper fraction = \(\frac{12}{8}\)
Total cups of dried fruit Jana have = 3\(\frac{12}{8}\)
= \(\frac{36}{8}\) = 4\(\frac{4}{8}\)
Question 12.
Critique Reasoning Kevin writes 1\(\frac{3}{6}\) + 2\(\frac{4}{6}\) = \(\frac{13}{6}\) + \(\frac{24}{6}\) = \(\frac{37}{6}\) = 6\(\frac{1}{6}\) . What does Kevin do wrong? Find the correct sum by changing the mixed numbers to fractions.
Answer:
Kevin add the whole number with numerator, instead of multiplying with the denominator.
Explanation:
Correct solution follows as shown below,
1\(\frac{3}{6}\) + 2\(\frac{4}{6}\) = \(\frac{9}{6}\) + \(\frac{16}{6}\) = \(\frac{25}{6}\) = 4\(\frac{1}{6}\)
Find the difference. If possible, write your answer as a mixed number.
Question 13.
2\(\frac{6}{10}\) – 1\(\frac{4}{10}\) = ____________
Answer:
1\(\frac{2}{10}\)
Explanation:
2\(\frac{6}{10}\) – 1\(\frac{4}{10}\)
convert into improper fraction
\(\frac{26}{10}\) – \(\frac{14}{10}\)
\(\frac{12}{10}\) = 1\(\frac{2}{10}\)
Question 14.
5\(\frac{7}{8}\) – 5\(\frac{1}{8}\) = __________
Answer:
\(\frac{6}{8}\) = \(\frac{3}{4}\)
Explanation:
5\(\frac{7}{8}\) – 5\(\frac{1}{8}\)
convert into improper fraction
\(\frac{47}{8}\) – \(\frac{41}{8}\)
\(\frac{6}{8}\) = 1\(\frac{3}{4}\)
Question 15.
2\(\frac{5}{6}\) – 1\(\frac{1}{6}\) = ___________
Answer:
1\(\frac{4}{6}\)
Explanation:
2\(\frac{5}{6}\) – 1\(\frac{1}{6}\)
convert into improper fraction
\(\frac{17}{6}\) – \(\frac{7}{6}\)
\(\frac{10}{6}\) = 1\(\frac{4}{6}\)
Question 16.
3\(\frac{9}{12}\) – 2\(\frac{8}{12}\) = ___________
Answer:
1\(\frac{1}{12}\)
Explanation:
3\(\frac{9}{12}\) – 2\(\frac{8}{12}\)
convert into improper fraction
\(\frac{45}{12}\) – \(\frac{32}{12}\)
\(\frac{13}{12}\) = 1\(\frac{1}{12}\)
I’m in a Learning Mindset!
How do I choose effective strategies to add and subtract mixed numbers?
Answer:
By observing the denominators, whether they are like fractions or unlike fractions.
Explanation:
The most effective strategy to add and subtract mixed numbers is to first convert into like fraction,
by taking LCD or LCM of the denominators.